Movimiento Armónico Simple - Ejercicios Resueltos

Uno de los temas más importantes dentro de la física, es el movimiento armónico simple (MAS), un movimiento periódico que se repite en intervalos iguales de tiempo. Este fenómeno puede ser descrito en función del movimiento circular uniforme, tomándolo en cuenta como la proyección sobre cualquier diámetro de un punto que se mueve en una trayectoria circular con cierta velocidad, cuya magnitud permanece constante. Tal como podemos ilustrar en la siguiente imagen.

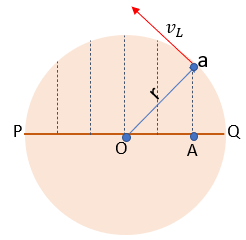
Si observamos bien, nos daremos cuenta de que:

El punto “a” se puede mover alrededor del círculo de radio r con una magnitud constante de velocidad “v”; si en cada intervalo de tiempo se traza una perpendicular desde el punto “a” hasta el diámetro P-Q (líneas punteadas), el punto “A” de la intersección se moverá con movimiento armónico simple a uno y otro lado de la línea recta desde P hasta Q.

Si analizamos bien, las líneas punteadas representan ese momento de velocidad donde aumenta y disminuye conforme al movimiento del punto “a”. Nos damos cuenta de que cuando está en el origen o sea en el centro “O”, la velocidad es máxima y cuando está en los extremos P-Q la velocidad es nula. Y así irá aumentando y disminuyendo hasta llegar a 0 en el otro extremo de la trayectoria.

Es lógico que cuando la magnitud de la velocidad va cambiando, exista también una aceleración. Dicha aceleración siempre se dirige a la posición central de equilibrio y su magnitud varía de la siguiente forma: cuando tenemos al movimiento en cualquiera de los extremos P o Q hacia el centro o punto 0, en los extremos se obtiene la mayor magnitud de la aceleración, la cual disminuye a medida que se acerca al centro donde se hace nula.

En resumen:

Cuando el punto “a” está en el centro, la velocidad es máxima y la aceleración es nula, y en los extremos la aceleración es máxima y la velocidad será nula.

Veamos algunos conceptos a utilizar en este tema del MAS

Elongación y Amplitud

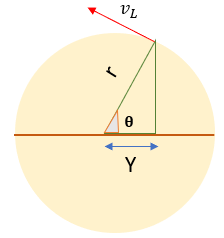
La elongación es la distancia de una partícula a su punto de equilibrio, esta puede ser positiva o negativa según esté hacia la derecha o a la izquierda de la posición de equilibrio.

La amplitud es la máxima elongación cuyo valor es igual al radio de la circunferencia.

Para poder obtener la fórmula de la amplitud o elongación de una partícula oscilatoria en cualquier instante tiempo “t” se usa la siguiente expresión:

O también:

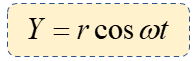
Dónde:

Y = elongación de la partícula en metros.

r = radio de la circunferencia en m

f = frecuencia en ciclos/s

t = tiempo en segundos (s)

ω = magnitud de la velocidad angular en rad/s

Velocidad de oscilación

La velocidad de oscilación de la partícula que describe dicho movimiento está dada sobre la proyección de la velocidad lineal del movimiento circular de un móvil sobre el diámetro de la circunferencia, como se expresa en la siguiente imagen.

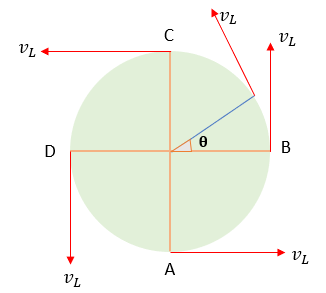
De la imagen podemos observar lo siguiente,

La velocidad de oscilación de la partícula que describe el movimiento armónico simple será positiva si va a la derecha, es decir, de D a B y negativa si va a la izquierda es decir de B a D.

Su fórmula para calcular será la siguiente:

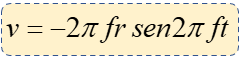
O también:

Donde:

v = magnitud de velocidad de oscilación en m/s

f = frecuencia en ciclos/s

r = radio de la circunferencia en metros (m)

t = tiempo en segundos (s)

Note también que cuando la velocidad lineal es paralela al diámetro (A y C) la velocidad de oscilación del cuerpo será la mayor y será igual a la velocidad lineal, ahora también cuando la velocidad lineal es perpendicular al diámetro (B y D) su proyección sobre el diámetro es nula, por lo tanto, su magnitud será de cero.

Aceleración de la partícula oscilante

En el movimiento armónico simple, la aceleración de una partícula oscilante es igual a la proyección sobre el diámetro de la aceleración radial, del movimiento circular uniforme de un móvil. Tal como podemos apreciar en la siguiente imagen:

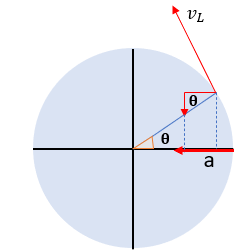
Y está dada por la siguiente ecuación:

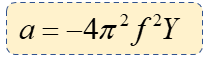
Donde:

a = magnitud de la aceleración en m/s^2

f = frecuencia en ciclos/s

Y = elongación en metros (m)

Para entender mucho mejor este tema, es conveniente resolver algunos ejercicios.

Ejercicios Resueltos de MAS (Movimiento Armónico Simple)

Solución:

Lo primero que debemos de anotar, son nuestros datos:

r = 0.2 m

T = 3 s

Lo primero que haremos será convertir el periodo a frecuencia.

$\displaystyle f=\frac{1}{T}=\frac{1}{{0.3s}}=0.33\frac{{ciclos}}{s}$

a) 

Una vez obtenida la frecuencia, es momento de calcular la elongación a los 6 segundos.

$\displaystyle Y=r\cos 2\pi ft$

Sustituyendo los datos en la fórmula:

$\displaystyle Y=(0.2m)\cos \left[ {2\pi \left( {0.33} \right)(6s)} \right]$

$\displaystyle Y=(0.2m)\cos \left[ {2\left( {3.14} \right)\left( {0.33} \right)(6s)} \right]$

$\displaystyle Y=(0.2m)\cos \left( {12.43rad} \right)$

Convertimos los radianes a grados:

$\displaystyle 12.43rad\left( {\frac{{57.3{}^\circ }}{{1rad}}} \right)=712.24{}^\circ $

Ahora si podemos colocarlo dentro del argumento del coseno

$\displaystyle Y=(0.2m)\cos \left( {712.24{}^\circ } \right)$

Multiplicando, obtenemos:

$\displaystyle Y=0.198m$

Por lo que nuestra elongación es de 0.198 metros.

b)

Ahora vamos a calcular la velocidad a los 6 segundos, aplicamos la fórmula:

$\displaystyle v=-2\pi frsen2\pi ft$

Recordemos que el valor de 2πft ya lo calculamos en el inciso a) que nos dio 712.24°, así que:

$\displaystyle v=-2\pi frsen\left( {712.24{}^\circ } \right)$

Ahora sustituimos los datos que tenemos en la nueva fórmula:

$\displaystyle v=-2(3.14)(0.33)(0.2)sen\left( {712.24{}^\circ } \right)$

Esto nos daría:

$\displaystyle v=-0.4145sen\left( {712.24{}^\circ } \right)$

Obteniendo el seno y multiplicando:

$\displaystyle v=0.056\frac{m}{s}$

Por lo que la velocidad es de 0.056 m/s

c)

Ahora vamos a calcular la magnitud de su velocidad máxima.

Aquí debemos ser cuidados, ya que la magnitud de la velocidad máxima se alcanza cuando el cuerpo está pasando por su punto de equilibrio y la elongación es cero, y eso solo ocurre cuando se presenta un ángulo de 90° o de 270°.

Entonces, aplicamos la fórmula:

$\displaystyle v=-2\pi frsen\left( {90{}^\circ } \right)$

Sustituyendo datos:

$\displaystyle v=-2(3.14)(0.33)(0.2m)sen(90)$

$\displaystyle v=-0.4145\frac{m}{s}$

La velocidad máxima es de -0.4145 m/s, si hubiéramos tomado al ángulo de 270°, tendríamos a la velocidad máxima positiva.