Solución Problema 1 Ley de Gay - Lussac

Vamos a resolver el ejercicio propuesto para reforzar los conocimientos adquiridos en el tema de La Ley de Gay - Lussac en el área de la teoría cinética de los gases, con este ejemplo resuelto el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado.

Nivel de Dificultad: ⭐⭐⭐

Problema 5. En un cilindro metálico se encuentra un gas que recibe una presión atmosférica de 760 mm de Hg, y cuando su temperatura es de 10°C , con el manómetro se registra una presión de 950 mm de Hg. Si al exponer el cilindro a la intemperie eleva su temperatura a 45°C debido a los rayos del sol, calcular:

a) ¿Cuál es la presión absoluta que tiene el gas encerrado en el tanque?

b) ¿Cuál es la presión manométrica?

Problema de Gay Lussac 1

Solución:

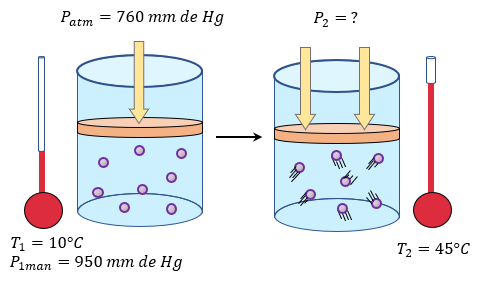
En este problema vemos que se habla de una presión atmosférica y de una presión manométrica, pero ambas son en condiciones iniciales (antes de exponer el cilindro a los rayos del sol), por lo que nos piden calcular dos puntos importantes:

La presión absoluta final (cuando se expone al sol)
La presión manométrica final (cuando se expone al sol)

Datos:

$\displaystyle {{P}_{atm}}=760mm\,de\,Hg$

$\displaystyle {{P}_{1man}}=950mm\,de\,Hg$

$\displaystyle {{T}_{1}}=10{}^\circ C+273=283K$

$\displaystyle {{T}_{2}}=45{}^\circ C+273=318K$

Recordemos que en la Ley de Gay Lussac se deben tomar cantidades absolutas en las temperaturas, es por eso que hemos sumado 273 a los grados celcius, para tener una escala absoluta de temperatura, y así resolver sin complicaciones nuestro ejemplo.

a) Obteniendo la presión absoluta final

Para poder obtener la presión absoluta final, es necesario conocer la presión absoluta inicial, ¿cómo la obtenemos?, aplicamos la siguiente fórmula:

$\displaystyle {{P}_{1abs}}={{P}_{atm}}+{{P}_{1man}}$