Ley de Gay-Lussac - Ejercicios Resueltos

Qué hay amigos, hoy hablaremos sobre otra ley muy importante en los gases y que de manera resumida y muy práctica la vamos a ver durante este post, así que toma asiento, cuaderno, lapicero y calculadora en mano que es momento de aprender algo nuevo, y eso algo nuevo es ni nada más ni nada menos que sobre la ley de gay-lussac .

bien, hasta este momento en el blog tenemos dos leyes relacionadas entre si que dan paso a ley general del estado gaseoso que se verá en otro post, por ahora ya se ha comprendido de que trata la ley de charles y la ley de boyle-mariotte y si no las has revisado pues no esperes más, y dales una checadita.

Entendiendo la Ley de Gay-Lussac

Vamos a lo que nos importa e interesa, esta ley tiene una particularidad en general al igual que las demás, por ejemplo; en la ley de charles la presión permanece constante, en la ley de boyle-mariotte es la temperatura quien permanece constante y para finalizar en la la ley de Gay-Lussac es el volumen quien permanece constante.

Antes de meternos en las matemáticas y fórmula de gay-lussac, veremos algo más sobre esta ley.

Aquí entenderemos porque la presión y temperatura van muy de la mano y son totalmente proporcionales, es decir, supongamos que acabas de comprar un aerosol, si sometemos ese aerosol a cierta temperatura de tal manera que aumente, la presión también aumentará, a esta relación se le llama proporcionalidad.

Notables científicos, físicos y químicos dedicaron parte de su tiempo para poder entender mejor esta ley, pero fue Gay-Lussac un físico-químico de origen Francés, que estudió a fondo el comportamiento de los gases respecto a la relación entre la presión y la temperatura, su ley estable lo siguiente.

Ahora si, vamos a lo matemático.

Fórmula de Gay-Lussac

Como dijimos texto atrás, la proporcionalidad que existe en esta ley es sobre la presión y la temperatura, matemáticamente colocaremos esto como:

$\displaystyle P\propto T$

Ahora introduzcamos una constante de proporcionalidad esto da paso a que se vea de la siguiente forma, es como un despeje simple.

$\displaystyle \frac{P}{T}=k$

Ahora al tratarse de una igualdad, podemos considerar las condiciones inicial y final, quedando la ecuación o fórmula matemática de la Ley de Gay-Lussac de la siguiente forma:

$\displaystyle \frac{{{P}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}}{{{T}_{2}}}$

donde:

$\displaystyle {{P}_{1}}=$ Presión Inicial

$\displaystyle {{T}_{1}}=$ Temperatura Inicial

$\displaystyle {{P}_{2}}=$ Presión Final

$\displaystyle {{T}_{2}}=$ Temperatura Final

Gráfica de la Ley de Gay-Lussac

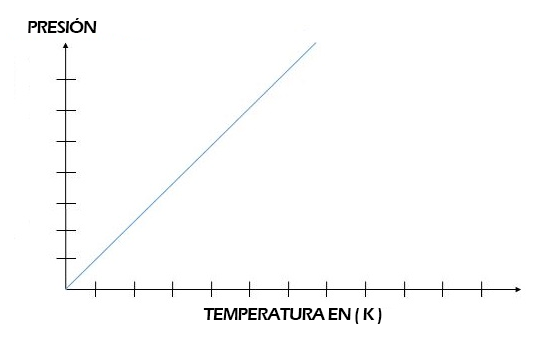
En la gráfica podremos observar claramente la proporcionalidad entre la presión y la temperatura, recordemos también que para las condiciones de un gas, las temperaturas deben darse en grados Kelvin.

Ejemplos resueltos de la Ley de Gay-Lussac

Solución: Si leemos detalladamente el problema nos podremos dar cuenta que las condiciones iniciales de temperatura y presión nos las dan como datos, al igual que la presión final, pero el único dato que no nos dan es la temperatura final, y la cual nos piden en °C.

Vamos a colocar nuestros datos:

$\displaystyle {{P}_{1}}=$ 440 mm de Hg.

$\displaystyle {{T}_{1}}=$ 35°C + 273 = 308 °K

$\displaystyle {{P}_{2}}=$ 760 mm de Hg.

$\displaystyle {{T}_{2}}=$ ?

He sumado a 35° la cantidad de 273, para poder hacer la conversión a grados Kelvin. Es muy importante que lo conviertan sino no dará el resultado que esperamos.

Ahora, usamos la fórmula para esta ley, la cual colocaré de nuevo.

$\displaystyle \frac{{{P}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}}{{{T}_{2}}}$

Despejando a $\displaystyle {{T}_{2}}$

Nos queda

$\displaystyle {{T}_{2}}=\frac{{{P}_{2}}{{T}_{1}}}{{{P}_{1}}}$

Ahora sustituimos nuestros datos.

$\displaystyle {{T}_{2}}=\frac{(760mmdeHg)(308{}^\circ K)}{440mmdeHg}=532{}^\circ K$

Pero nos piden el resultado en °C, por lo que restaremos 273 a la cantidad resultante en grados Kelvin.

$\displaystyle {{T}_{2}}=532{}^\circ K-273=259{}^\circ C$

Como podemos observar en las condiciones iniciales del problema, la temperatura aumentó y como resultado también la presión, esto quiere decir que hemos resuelto el problema con éxito.

Veamos otro ejemplo:

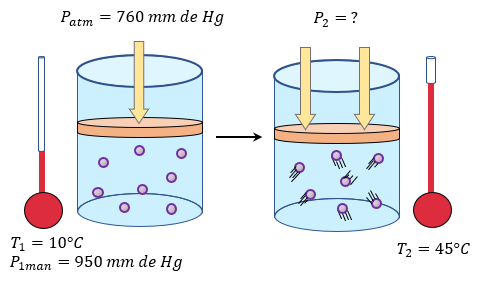
Solución: Para este ejemplo podemos observar claramente que la variable que nos hace alta es la presión final, por lo que haremos una recopilación de nuestros datos y empezar a resolver.

Si hacemos el análisis también nos damos cuenta que la temperatura ha aumentado de 45°C a 125°C esto quiere decir que por la proporcionalidad que existe entre la presión y temperatura, la presión aumentará como resultado final, no sabemos en que cantidad, pero si sabemos que aumentará.

¡Muy importante! y vuelvo a repetirlo, la temperatura siempre será en escala absoluta, es decir grados Kelvin.

Datos:

$\displaystyle {{P}_{1}}=$ 460 mm de Hg.

$\displaystyle {{T}_{1}}=$ 45°C + 273 = 318 °K

$\displaystyle {{P}_{2}}=$ ?

$\displaystyle {{T}_{2}}=$ 125°C + 273 =398°K

Por fórmula tenemos

$\displaystyle \frac{{{P}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}}{{{T}_{2}}}$

Despejando $\displaystyle {{P}_{2}}$

Nos queda

$\displaystyle {{P}_{2}}=\frac{{{P}_{1}}{{T}_{2}}}{{{T}_{1}}}$

Reemplazando nuestros datos en la fórmula

$\displaystyle {{P}_{2}}=\frac{(460mmdeHg)(398{}^\circ K)}{318{}^\circ K}=575.72mmdeHg$

Pero, para entenderlo mejor sigamos viendo un tercer ejemplo más 😎

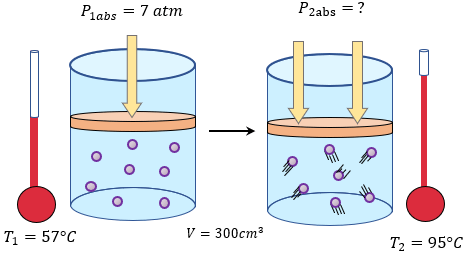
Solución: Anotemos los datos de nuestro problema y veamos las variables que tenemos y la que nos hace falta, recordemos mantener a la temperatura en su escala absoluta, por lo que tenemos que convertir a Kelvin.

$\displaystyle {{P}_{1}}=2atm$

$\displaystyle {{T}_{1}}=27{}^\circ C$

$\displaystyle {{P}_{2}}=3atm$

$\displaystyle {{T}_{2}}=?$

Convertimos a la temperatura 1, en absoluta, quedando así:

$\displaystyle {{T}_{1}}=27+273=300{}^\circ K$

Ahora, nos damos cuenta que nos hace falta la temperatura final, o T2, por lo que procedemos a realizar el despeje de la fórmula.

$\displaystyle {{T}_{2}}=\frac{{{P}_{2}}{{T}_{1}}}{{{P}_{1}}}$

Sustituyendo en nuestros datos:

$\displaystyle {{T}_{2}}=\frac{{{P}_{2}}{{T}_{1}}}{{{P}_{1}}}=\frac{(3atm)(300{}^\circ K)}{2atm}=450{}^\circ K$

Por lo que la temperatura aumentó a 450°K, por lo que tiene lógica, ya que si vemos el aumento de la temperatura, se debe al aumento de la presión.

Solución: Nuevamente debemos recopilar nuestros datos, y a su vez recordar en convertir la temperatura que está en Celcius y pasarlas a Kelvin, así que aquí vamos.

$\displaystyle {{P}_{1}}=4atm$

$\displaystyle {{T}_{1}}={{47}^{{}^\circ }}C$

$\displaystyle {{P}_{2}}=?$

$\displaystyle {{T}_{2}}=127{}^\circ C$

Pasando a temperatura absoluta a nuestras temperaturas tenemos que:

$\displaystyle {{T}_{1}}=47+273=320{}^\circ K$

$\displaystyle {{T}_{2}}=127+273=400{}^\circ K$

Ahora despejamos de nuestra fórmula a la presión final o P2.

$\displaystyle {{P}_{2}}=\frac{{{P}_{1}}{{T}_{2}}}{{{T}_{1}}}=\frac{(4atm)(400{}^\circ K)}{320{}^\circ K}=5atm$

Por lo que la presión final es de 5 atmósferas ¿complicado?, seguro que no, no es complicado. Recuerda practicar y resolver más ejercicios para que aprendas de una vez por todas. 😎

? Ejercicios para Practicar de Gay - Lussac

Resuelva los siguientes ejercicios y compruebe los resultados paso a paso haciendo click en la parte “ver solución”.  ??

? Ver Solución

? Ver Solución