Dilatación Volumétrica - Ejercicios Resueltos
Ya hemos hablado sobre la dilatación lineal, la dilatación superficial y ahora terminamos estos tres capítulos hablando de la dilatación cúbica o dilatación volumétrica que significan lo mismo. Para ello debemos de tener en cuenta que el proceso de dilatación cúbica hace referencia al aumento de las dimensiones de un objeto a lo largo, ancho y alto, o sea que en términos geométricos tenemos un incremento de volumen.
En este estudio hay que considerar el coeficiente de dilatación cúbica que nos hace hincapié al incremento relativo de volumen que experimenta un objeto de determinada sustancia, preferente de un volumen igual a la unidad, al elevar su temperatura un grado Celsius.
Este coeficiente se determina mediante la letra griega gamma $\displaystyle \gamma $.Por lo general este coeficiente de dilatación se usa para los líquidos, matemáticamente tenemos la relación de que la dilatación volumétrica es tres veces mayor que la dilatación lineal.
$\displaystyle \gamma =3\alpha $
Podemos hacer una comprobación muy sencilla , por ejemplo; si sabemos que el coeficiente de dilatación lineal del acero es $\displaystyle 12x{{10}^{-6}}{}^\circ {{C}^{-1}}$ , entonces el coeficiente de dilatación volumétrica sería:
$\displaystyle \gamma =3\alpha =3(12x{{10}^{-6}}{}^\circ {{C}^{-1}})=36x{{10}^{-6}}{}^\circ {{C}^{-1}}$
¿Se entendió?
Entonces dejamos la tabla para no tener problemas al resolver los ejercicios propuestos.
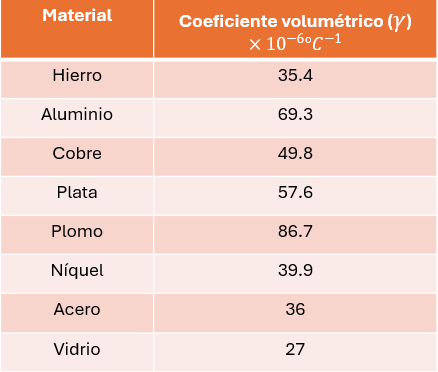
⭐ Tabla de Dilatación Cúbica o Volumétrica
Colocamos la siguiente tabla, y debemos considerarlo para la solución de los ejercicios propuestos más adelante.
Fórmula de Dilatación Volumétrica o Dilatación Cúbica
Como bien sabemos, al conocer la dilatación cúbica de cualquier sustancia, entonces podemos calcular el volumen final que tendrá la sustancia, mediante la siguiente fórmula.
$\displaystyle {{V}_{f}}={{V}_{0}}\left[ 1+\gamma \left( {{T}_{f}}-{{T}_{0}} \right) \right]$
Dónde:
$\displaystyle {{V}_{f}}$ = Volumen Final en Metro Cúbico
$\displaystyle {{V}_{0}}$ = Volumen Inicial en Metro Cúbico
$\displaystyle \gamma $ = Coeficiente de Dilatación Cúbica
$\displaystyle {{T}_{f}}$ = Temperatura Final en Grados Celcius
$\displaystyle {{T}_{0}}$ = Temperatura Inicial en Grados Celcius
Consejos Importantes para resolver problemas de Dilatación Cúbica
Antes de resolver algunos ejemplos resueltos, necesitamos forzosamente tener en cuenta las siguientes anotaciones.
- Consejo 1.- En el caso de los sólidos que no están uniformes, es decir; aquellos sólidos que poseen algún hueco en su textura, debe considerarse como si estuviera lleno del mismo material, es decir, como si fuera totalmente sólido.
- Consejo 2.- Para la dilatación cúbica en los líquidos hay que tomar en cuenta que cuando se ponen a calentar, también se calienta el recipiente que los posee, el cual al dilatarse aumenta también su capacidad calorífica. Por ello, el aumento real del volumen del líquido será igual al incremento de volumen del objeto que los contiene o sea el recipiente más el aumento del volumen del líquido en el recipiente graduado.
- Consejo 3.- El coeficiente de dilatación volumétrica es igual para todos los gases, ¿ por qué? porque, al ser sometido a una presión constante, por cada grado Celsius que cambie su temperatura variará 1/273 el volumen que ocupaba a 0° celcius.
Ejercicios Resueltos de Dilatación Volumétrica
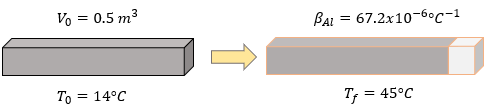
Solución:
Datos:
Coeficiente volumétrico del aluminio: \( \gamma = 69.3 \times 10^{-6} \, {}^{\circ} \text{C}^{-1} \),
Volumen inicial: \( V_0 = 0.5 \, \text{m}^3 \),
Temperatura inicial: \( T_0 = 14^{\circ} \text{C} \),
Temperatura final: \( T_f = 45^{\circ} \text{C} \).
Aplicando la fórmula de dilatación volumétrica:
\[
V_f = V_0 \left[ 1 + \gamma (T_f - T_0) \right]\]\[
V_f = 0.5 \, \text{m}^3 \left[ 1 + 69.3 \times 10^{-6} \, {}^{\circ} \text{C}^{-1} \times (45^{\circ} \text{C} - 14^{\circ} \text{C}) \right]\]\[
V_f = 0.5 \, \text{m}^3 \left[ 1 + 69.3 \times 10^{-6} \times 31 \right]\]\[
V_f = 0.5 \, \text{m}^3 \left[ 1 + 0.0021483 \right] = 0.5 \, \text{m}^3 \times 1.0021483 = 0.50107415 \, \text{m}^3
\]
Volumen final (redondeado):
\[
V_f \approx \boxed{0.501 \, \text{m}^3}
\]
Incremento de volumen:
\[
\Delta V = 0.50107415 \, \text{m}^3 - 0.5 \, \text{m}^3 = \boxed{0.001 \, \text{m}^3}
\]
Solución:
Datos:
Coeficiente volumétrico del vidrio: \( \gamma = 27 \times 10^{-6} \, {}^{\circ} \text{C}^{-1} \) (\( \alpha = 9 \times 10^{-6} \)),
Volumen inicial: \( V_0 = 0.8 \, \text{m}^3 \),
Temperatura inicial: \( T_0 = 25^{\circ} \text{C} \),
Temperatura final: \( T_f = 5^{\circ} \text{C} \).
Fórmula de dilatación volumétrica:
\[
V_f = V_0 \left[ 1 + \gamma (T_f - T_0) \right]\]
Procedemos a realizar los cálculos:
\[
\Delta T = 5^{\circ} \text{C} - 25^{\circ} \text{C} = -20^{\circ} \text{C}
\]\[
V_f = 0.8 \, \text{m}^3 \left[ 1 + 27 \times 10^{-6} \times (-20) \right]\]\[
V_f = 0.8 \, \text{m}^3 \left[ 1 - 0.00054 \right] = 0.8 \, \text{m}^3 \times 0.99946 = 0.799568 \, \text{m}^3
\]
Resultados (redondeados a 4 decimales):
\[
V_f \approx \boxed{0.7996 \, \text{m}^3}, \quad \Delta V \approx \boxed{-0.0004 \, \text{m}^3} \quad \text{(contracción)}
\]
Ejercicios para Practicar de Dilatación Volumétrica
A continuación se muestran algunos ejercicios adicionales de dilatación volumétrica o dilatación cúbica para reforzar el aprendizaje de éste tema, así mismo se incluyen las soluciones paso a paso, para poder ver las soluciones debe dar click en el texto "Ver Solución".
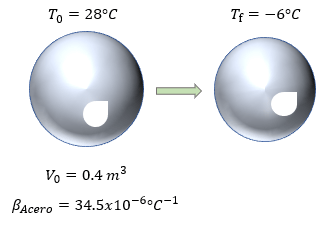
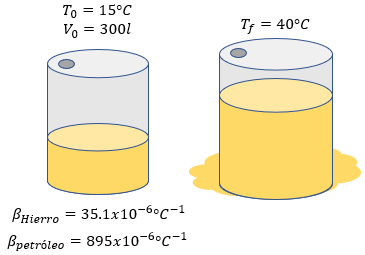
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Tengo una duda, ¿cual es la dilatacion volumetrica del Zinc? Gracias.
-
Cual es la variación de temperatura de una barra de plata de dilata o.4ml y cuya longitud inicial es 43cm
-
una barra de oro de 20° c tiene las siguientes dimensiones:20 cm de largo, 10 cm de ancho y 5 cm de profundidad. cual sera su expansión después de ser sometido a 50° c de temperatura. suponga que el coeficiente del oro es de 15x10^6
47 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar