Calor Específico - Ejercicios Resueltos

Uno de los temas más destacados e importantes en calorimetría es el tema de Calor Específico, pero antes de hablar sobre el calor específico necesitamos conocer sobre el Calor Sensible y el Calor Latente, finalmente después de comprender estos términos, podremos resolver ejercicios o problemas de este tema, y adicionalmente resolveremos más ejercicios propuestos.

🔥 ¿Qué es el calor sensible y el calor latente?

Cuando un cuerpo recibe o cede cierta cantidad de energía térmica, podemos observar, como consecuencia, una variación de su temperatura o un cambio en su estado físico.

La variación de temperatura corresponde a una variación en el estado de agitación de las partículas del cuerpo. En este caso, la energía térmica transferida se denomina calor sensible. El cambio de estado físico corresponde a un cambio en el estado de agregación de las partículas del cuerpo, haciendo que un sólido, por ejemplo, se transforme en líquido. La energía térmica responsable de los cambios de estado se denomina calor latente.

También es muy importante que quede bien claro la diferencia entre calor y temperatura. Calor es la denominación que damos a la energía térmica cuando, ella se encuentra transitando entre dos lugares de diferentes temperaturas. La temperatura es el estado termodinámico de un cuerpo que asociamos al nivel medio de agitación de sus partículas.

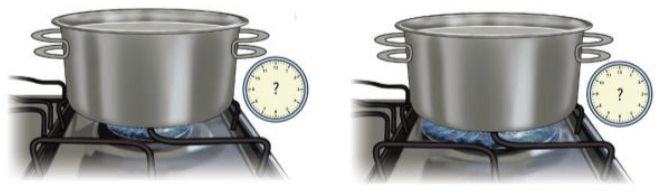
Si vemos la imagen, nos daremos cuenta de lo siguiente. La energía térmica suministrada por la llama de la estufa se utilizó inicialmente para calentar la tetera y el agua. Cuando ocurre la ebullición, observamos vapor de agua saliendo por el pico de la caldera. Este vapor es parte del agua que pasó al estado gaseoso.

🤔 ¿Qué es el Calor Específico?

Para entender al Calor Específico, es importante analizar muchos casos y situaciones. Para ello lo analizaremos poco a poco.

El efecto más claro para entender este fenómeno es el siguiente, ocurre cuando la variación de temperatura de un objeto se le suministra o retira energía térmica, o sea, cuando lo calentamos o lo enfriamos. Si colocamos una olla con agua en una estufa encendida, su temperatura aumenta. Si la colocamos dentro de un refrigerador o nevera, su temperatura disminuye. ¿Pero de qué dependen estas variaciones de temperatura? Es de eso que trataremos en este artículo.

Imagine las siguientes situaciones:

Caso 1: 

Tenemos dos ollas, una de hierro y otra de vidrio, conteniendo la misma cantidad de agua, se apoyan en dos quemadores de estufa diferentes. ¿Usted cree que habrá diferencia de temperaturas después de un mismo intervalo de tiempo?

Caso 2: 

Dos ollas idénticas, que contengan la misma cantidad de agua, se colocan al mismo tiempo en quemadores de estufas distintas, una con la llama  "baja" y la otra con la llama "alta". Usted cree que ¿habrá diferencia en el tiempo para hervir el agua?

Caso 3: 

Nuevamente, tenemos dos ollas y ambas son idénticas, una conteniendo 1 litro de agua y la otra 1/2 litro, se colocan en quemadores de estufas distintas. ¿Crees que una de ellas se hervirá primero que la otra?

Las comparaciones de los casos anteriores muestran que la elevación de temperatura de un cuerpo depende del material del que está hecho (Caso 1), también depende de la cantidad de calor suministrada (Caso 2) y de la cantidad de materia del cuerpo (Caso 3). Lo mismo ocurriría en caso del enfriamiento.

En cuanto al calor específico, nos da a entender cuando un material es más difícil tanto de calentar o enfriar, o sea, menor es su variación de temperatura cuando recibe o pierde una misma cantidad de calor o energía térmica. Podemos pensar en el calor específico como una medida de "resistencia" de una sustancia a cambiar de temperatura cuando cambio el calor.

En la primera situación, la olla de hierro alcanza una temperatura más elevada que la de vidrio porque el hierro tiene menor calor específico que el vidrio.

Se define calor específico (ce) como la cantidad de calor que necesita un gramo de una sustancia para elevar su temperatura a un grado centígrado. La unidad de medida del calor específico más comúnmente utilizada es cal / g ° C.

📈 Tabla de Calores Específicos

De esta tabla, es posible concluir que la variación de temperatura de un cuerpo, al intercambiar cierta cantidad de energía térmica, depende del material de que está constituido dicho cuerpo (calor específico) y de su masa.

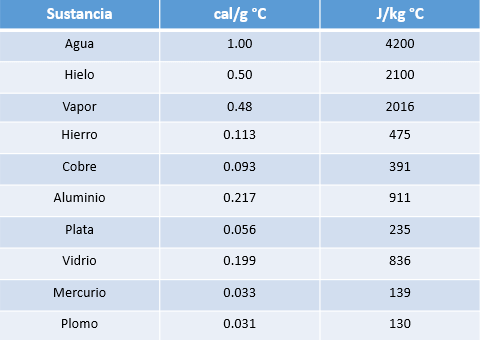
Podemos observar que el agua posee mayor calor específico, por lo que es más difícil de calentar.

🔹 Fórmula del Calor Específico

Matemáticamente expresamos al calor específico de la siguiente forma:

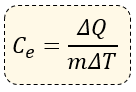
Dónde:

ΔQ = Incremento de Calor (se mide en calorías)

ΔT = Incremento de Temperatura (se mide en °C)

m = Masa (se mide en gramos)

En algunas ocasiones podemos encontrarnos la fórmula de la Capacidad Calorífica que es de donde proviene la fórmula del calor específico.

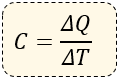
Dónde:

C = Capacidad calorífica (cal/°C)

ΔQ = Incremento de Calor (se mide en calorías)

ΔT = Incremento de Temperatura (se mide en °C)

🔸 Ejercicios Resueltos de Calor Específico

Para entender mucho mejor el tema de Calor Específico, veamos la solución de los siguientes problemas.

Solución:

El ejercicio es muy fácil de resolver, pues se cuenta con 600 gramos de hierro que inicialmente posee una temperatura de 19°C, y que se le suministra una cantidad de 1300 calorías, finalmente nos pide calcular la temperatura final, pero no olvidemos que se trata del calor específico del hierro. Así que retomando los datos tenemos.

Datos:

a) Obtener la temperatura final

Tenemos la fórmula del calor específico:

Despejando a la temperatura:

La variación de temperatura la podemos escribir de la siguiente manera:

Despejando a la temperatura final "Tf"

Ahora si podemos sustituir nuestros datos en la fórmula, de la siguiente forma:

Realizando la multiplicación del denominador, obtenemos.

Dividiendo:

Sumando:

Por lo que el resultado de la temperatura final es de 38.17°C

Solución:

A diferencia del primer problema, vemos que en este problema nos piden encontrar la cantidad de calor necesaria para elevar la temperatura de 24 kg de plata de 31°C hasta 110°C, pero también debemos de tener en cuenta que se trata de una barra de plata. No olvide convertir la masa en gramos.

Datos:

a) Obteniendo la cantidad de calor para la barra de Plata

De la fórmula de calor específico tenemos:

Como el problema nos pide encontrar la cantidad de calor, la vamos a despejar.

A la temperatura también la podemos escribir de esta forma:

Ahora si podemos sustituir nuestros datos en la fórmula:

Realizando la resta de temperaturas:

Multiplicando las unidades, obtenemos:

Esto nos da un total de 106176 calorías para que ocurra todo el proceso que nos pide el problema.

Solución:

Al igual que el problema anterior, en este problema nos pide calcular la cantidad de calor, solo que este calor no se suministra sino que es un calor que se cede al ambiente porque la temperatura desciende de 130°C hasta los 10°C. El material que es sometido se trata de la plata, por lo tanto hay que tener en cuenta su calor específico.

Datos:

a) Obtener la cantidad de calor cedido

Aplicamos la fórmula del calor específico, pero recordemos que en el problema anterior ya hemos despejado a la variable ΔQ, esto es:

Qué también la podemos escribir de la siguiente manera:

Sustituyendo los datos en la fórmula:

Resolviendo la diferencia de temperaturas:

Multiplicando, finalmente obtenemos:

Lo que es un valor de -34,944 calorías

Nota: El signo negativo (-) que hemos obtenido en el resultado, nos indica la disminución de la temperatura puesto que el cuerpo empezó a ceder calor al ambiente.

📃 Ejercicios Para Practicar de Calor Específico

Ahora es momento de practicar con algunos ejemplos y problemas propuestos. Cada uno tiene su propia solución para verificar si ha llegado al resultado correcto. 😊👇

👉 Ver Solución

👉 Ver Solución

👉 Ver Solución