Dilatación Lineal, Superficial, y Volumétrica - Ejercicios Resueltos

Heeeeeey!! qué tal amigos, hoy les traigo un post pero muy bueno sobre la dilatación lineal, terminando éste post puedes pasar por la dilatación superficial, y finalmente con la dilatación cúbica o volumétrica. Bien, pues la dilatación lineal es el principio nos abre un poco la mente para conocer que no solo los sólidos se dilatan, sino también los gases, y líquidos, pero esta vez nos enfocaremos en la dilatación de los sólidos.

• Ver ejercicios resueltos de dilatación superficial
• Ver ejercicios resueltos de dilatación volumétrica

Con mucho trabajo y proyectos en puerta, cuesta escribir en detalle, por lo que por ahora nos centraremos en la dilatación lineal, así que comenzamos. ¡Toma asiento, libreta y lápiz en mano!, claro sin dejar a un lado la calculadora y un poco de lógica... vamos a ello. ??

¿Qué es la dilatación lineal?

La dilatación es un efecto natural muy conocido y que ocurre cuando las dimensiones de los cuerpos aumentan en presencia de la elevación de la temperatura, salvo algunas excepciones que veremos mucho más adelante o quizá en otro post. Lo curioso de la dilatación es que cuando este fenómeno ocurre, después de cierto tiempo y que la temperatura vuelve a su estado original o normal, todo cuerpo dilatado vuelve a su estado inicial.

Podemos apreciar un ejemplo muy claro en las juntas que se dejan en algunas carreteras, pues es muy común en el cemento o estructuras de construcción.

Un ejemplo aún más claro, es en las vías del tren. Si nosotros caminos a un lugar donde pasa el ferrocarril lo observaremos y apreciaremos mejor. Dicha junta es también colocada por efectos de la dilatación lineal:

¿Por qué ocurre la dilatación?

Si bien la dilatación es un fenómeno natural pero con una determinada explicación, y esto se basa desde su origen, es decir; todo lo que ocupa un lugar en el espacio tiene masa y a su vez esta formada por un conjunto de átomos.

Al conservar esa estructura, los átomos al elevarse la temperatura tienden a separarse a cierta distancia unos a otros, eso ocasiona que el sólido aumente de tamaño, es decir: que se dilate...!

Hagamos ahora el siguiente análisis con una barra de aluminio.

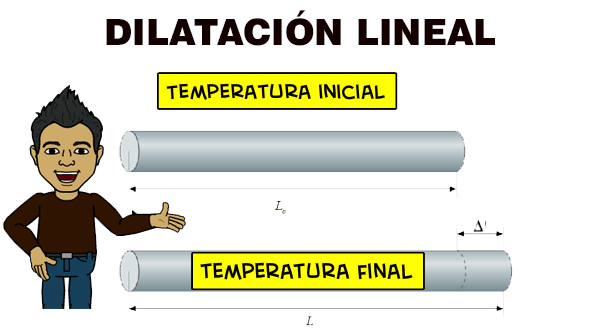
Yo se que a más de uno, las ecuaciones le causan mucha confusión, pero es fácil poder analizarlo, veamos lo siguiente. 🙂

Al analizar el fenómeno, establezcamos que la barra de aluminio está en condiciones iniciales, es decir, a temperatura inicial, y longitud inicial.

Para ello, le pongamos nombre.

$\displaystyle {{L}_{o}}=$ Longitud Inicial

$\displaystyle {{t}_{o}}=$ Temperatura Inicial

Por lo contrario

$\displaystyle L=$ Longitud Final

$\displaystyle t=$ Temperatura Final

Entonces, una variación de temperatura produce una dilatación.

Los científicos empezaron a medir distintas barras con diferente material para ver el comportamiento que tenían al someterse a diferentes cambios de temperatura, entonces se dieron cuenta que la dilatación, depende de la longitud inicial y del aumento de temperatura, siendo proporcional a ambos, es decir.

$\displaystyle \Delta L=\alpha {{L}_{o}}\Delta t$  --> Ecuación Principal

Esto quiere decir que, esa ecuación nos permite calcular la dilatación de cualquier dimensión lineal...

Sin embargo para fines de los ejercicios aquí resueltos, vamos a usar esa misma fórmula pero más desglosada.

La diferencia de longitud, entra la final y la inicial está dada por la ecuación:

$\displaystyle \Delta L={{L}_{f}}-{{L}_{o}}$

Reemplazando este valor en nuestra ecuación principal

Ahora esto nos queda.

$\displaystyle {{L}_{f}}-{{L}_{o}}=\alpha {{L}_{o}}\Delta t$

Despejando la longitud final.

$\displaystyle {{L}_{f}}={{L}_{o}}+\alpha {{L}_{o}}\Delta t$

Factorizando el segundo miembro

$\displaystyle {{L}_{f}}={{L}_{o}}(1+\alpha \Delta t)$

Recordar también que;

$\displaystyle \Delta t={{t}_{f}}-{{t}_{o}}$

Es decir, la temperatura final menos la temperatura inicial, nos da la diferencial de temperatura.

En la fórmula también observamos una letra del alfabeto griego, "alfa"  $\displaystyle \alpha $

Esa constante de proporcionalidad, la reemplazaremos por cualquier coeficiente de dilatación lineal, es decir; el aluminio, el cobre, el vidrio común tienen distintas constantes de dilatación, pues no todos alcanzan la misma longitud al dilatarse, algunos más que otros, y otros menos.

Fórmula de Dilatación Lineal

De forma resumida, la fórmula de dilatación lineal es la siguiente:

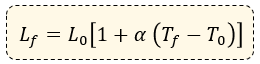
Es la forma más concisa para encontrar la longitud final (por dilatación).

Para encontrar el coeficiente de dilatación lineal se emplea:

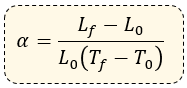
Tabla de Sustancias con Coeficientes de Dilatación Lineal

Actualmente existen diversas tablas para guiarnos en la solución de problemas de éste tipo de dilatación.

Veamos entonces la siguiente tabla:

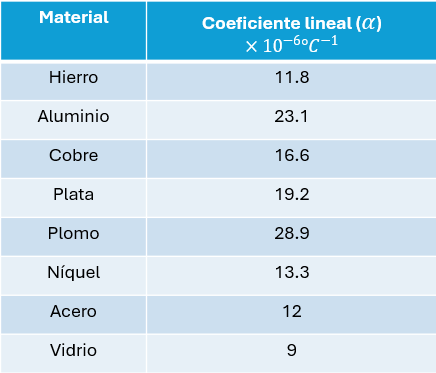
Ahora veamos los siguientes ejercicios resueltos paso a paso.

Ejercicios resueltos de Dilatación Lineal

Solución: El problema es muy sencillo, por lo cual no requiere mucho análisis, sin embargo vamos a tocar ese punto antes de comenzar a resolverlo.

Si bien se sabe, los rieles en las vías del ferrocarril, normalmente se le coloca un espacio entre ellas a cierta distancia para cuando éste material se dilate a ciertas horas del día.

Ahora anotemos nuestros datos:

Datos:

$\displaystyle {{L}_{o}}=1500m$ --> Longitud Inicial

$\displaystyle {{L}_{f}}=\text{?}$ --> Longitud Final  --> La vamos a encontrar

$\displaystyle {{t}_{o}}=24{}^\circ C$ --> Temperatura Inicial

$\displaystyle {{t}_{f}}=45{}^\circ C$ --> Temperatura Final

$\displaystyle \alpha =11x{{10}^{-6}}{}^\circ {{C}^{-1}}$  --> Coeficiente de dilatación lineal del Acero.

Hemos elegido acero, porque el problema nos pide que son vías del ferrocarril de acero.

Lo único que haremos será sustituir nuestros datos, en la fórmula final.

$\displaystyle {{L}_{f}}={{L}_{o}}(1+\alpha \Delta t)$

Pero antes de sustituir, debemos saber cual es el valor de la diferencial de temperatura, para poder meterla en la fórmula, esa diferencial es la resta de la temperatura más alta, con la temperatura más baja.

$\displaystyle \Delta t=45{}^\circ C-24{}^\circ C=21{}^\circ C$

Ahora si, a sustituir en la fórmula.

$\displaystyle {{L}_{f}}=1500m(1+21{}^\circ C\cdot 11x{{10}^{-6}}{}^\circ {{C}^{-1}})$

$\displaystyle {{L}_{f}}=1500m(1+2.31x{{10}^{-4}})$

$\displaystyle {{L}_{f}}=1500m(1.000231)$

Resultado:

$\displaystyle {{L}_{f}}=1500.3465m$

Si observamos, las vías del tren se han dilatado solo .3465 metros, es decir 346.5 milimetros, muy poco, pero significativo para la distancia entre las juntas de riel.

Ahora veamos otro ejemplo 😎

Solución: El problema nos pide la temperatura final de un cuerpo de plomo cuando éste alcanza una longitud final de 25.43, para ello vamos a considerar primeramente nuestros datos:

$\displaystyle {{L}_{o}}=25.34m$ --> Longitud Inicial

$\displaystyle {{L}_{f}}=25.43m$ --> Longitud Final

$\displaystyle {{t}_{o}}=26{}^\circ C$ --> Temperatura Inicial

$\displaystyle {{t}_{f}}=x{}^\circ C$ --> Temperatura Final (La que vamos a encontrar)

$\displaystyle \alpha =29x{{10}^{-6}}{}^\circ {{C}^{-1}}$  --> Coeficiente de dilatación lineal del Plomo.

Ahora solamente tenemos que despejar nuestra fórmula en términos de la temperatura final.

$\displaystyle {{L}_{f}}-{{L}_{0}}=\alpha {{L}_{0}}\Delta t$

$\displaystyle \frac{{{L}_{f}}-{{L}_{0}}}{\alpha {{L}_{0}}}=\Delta t$

Ahora tenemos que invertir la ecuación, para mayor comodidad

$\displaystyle \Delta t=\frac{{{L}_{f}}-{{L}_{0}}}{\alpha {{L}_{0}}}$

Posteriormente si sabemos que $\displaystyle \Delta t={{t}_{f}}-{{t}_{o}}$

Entonces

$\displaystyle {{t}_{f}}-{{t}_{o}}=\frac{{{L}_{f}}-{{L}_{0}}}{\alpha {{L}_{0}}}$

Despejando la temperatura final:

$\displaystyle {{t}_{f}}=\frac{{{L}_{f}}-{{L}_{0}}}{\alpha {{L}_{0}}}+{{t}_{0}}$

Ahora reemplazamos nuestros datos:

Solución:

$\displaystyle {{t}_{f}}=\frac{25.43-25.34}{(29x{{10}^{-6}})(25.34)}+26=148.4772{}^\circ C$

Por lo que tenemos una temperatura final de 148.4772°C

Y eso nos da a entender que justamente cuando el cuerpo alcanza cierta dilatación final de 25.34m, lo hace cuando la temperatura está a los 148.4772°C

😎

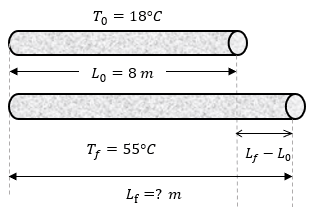
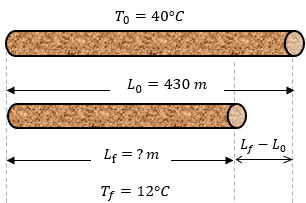
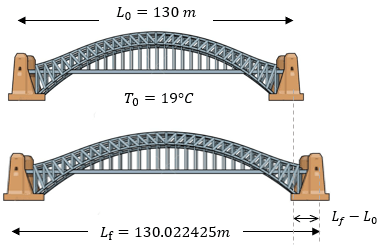
Ejercicios para Practicar de Dilatación Lineal

A continuación se colocan tres ejemplos resueltos para practicar y para que el estudiante verifique sus resultados viendo la solución correspondiente ??

Ver Solución 

Ver Solución

Ver Solución

Dilatación Superficial - Ejercicio Resuelto

Para poder ver ejercicios resueltos sobre dilatación superficial es necesario entrar en el siguiente vínculo:

 Ver ejercicios de dilatación superficial