Ley general del estado gaseoso

Cómo están [email protected]?? Hoy traigo un post que es de gran importancia para entender el comportamiento de los gases y que también cierra la saga de temas individuales por cada variable, es decir: temperatura, presión y volumen.

Entonces, vamos a comenzar. Nuevamente te pido que tomes asiento, papel, lápiz, calculadora, borrador y demás para poder comprender este tema.

Otra cosa, antes de poder iniciar, es necesario que sepas por lo menos de que va, la ley de Charles, la ley de Gay-Lussac y la ley de Boyle-Mariotte, ¿No tienes idea?, entonces te sugiero que los leas 🙂

🔹 Ecuación general del estado gaseoso

La ecuación general del estado gaseoso es una combinación de las ecuaciones antes mencionadas, donde nuevamente las variables a encontrar son la presión, temperatura o volumen del gas, cuando se tiene un cambio entre dos variables.

La expresión matemática, o fórmula de la ecuación general del estado gaseoso, es la siguiente:

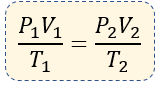
Fórmula general de la ley del estado gaseoso

\displaystyle \frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}

Dónde:

\displaystyle {{P}_{1}} = Presión Inicial

\displaystyle {{V}_{1}} = Volumen Inicial

\displaystyle {{T}_{1}} = Temperatura Inicial

\displaystyle {{P}_{2}} = Presión Final

\displaystyle {{V}_{2}} = Volumen Final

\displaystyle {{T}_{2}} = Temperatura Final

¡Recordar!, las temperaturas se manejan en escalas absolutas, es decir en °K

Pero como siempre, es mejor aprender las cosas mediante ejercicios resueltos, y aquí te presento algunos.

Cuando resuelva problemas, y lea el enunciado decir que un gas está a condiciones normales, quiere decir que el gas se considera a 0°C es decir a 273K, y a una presión de una atmósfera igual a 760 mm de Hg.

🔸 Ejercicios resueltos de la ley general del estado gaseoso

 Problema 1.- Un volumen de 450 ml de oxígeno fue tomado o colectado a 30°C y 480 mm de Hg. ¿Qué volumen ocupará el oxígeno al variar la temperatura a 45°C y una presión de 650 mm de Hg? 

Solución: 

Puede sonar confuso si no entendemos el problema, pero no es difícil si vamos considerando los datos que el mismo problema nos arroja. Cómo podrás darte cuenta hay un volumen inicial de la toma del oxígeno, así cómo una presión y temperatura y al final, nos preguntan sobre el volumen, es decir nuestra incógnita y a la vez dándonos dos datos más, la temperatura y presión final, por lo que ahora tomaremos esos datos:

\displaystyle {{P}_{1}} = 480 mm de Hg

\displaystyle {{V}_{1}} = 450 ml

\displaystyle {{T}_{1}} = 30° + 273 = 303 K

\displaystyle {{P}_{2}} = 650 mm de Hg

\displaystyle {{T}_{2}} = 45°C + 273 = 318 K

\displaystyle {{V}_{2}} = ???

Según nuestra fórmula:

\displaystyle \frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}

Despejaríamos la variable \displaystyle {{V}_{2}} de la ecuación.

\displaystyle {{V}_{2}}=\frac{{{P}_{1}}{{V}_{1}}{{T}_{2}}}{{{P}_{2}}{{T}_{1}}}

Por lo que si sustituimos, tendremos que:

\displaystyle {{V}_{2}}=\frac{(480mmHg)(450ml)(318K)}{(650mmHg)(303K)}=348.75ml

Veamos otro ejercicio.

 Problema 2.- Un gas ocupa un volumen de 300 ml a 35°C y 760 mm de Hg. Se comprime dentro de un recipiente de 100 ml de capacidad a una presión de 1.5 atm. ¿Cuál es la temperatura final del gas en °C? 

Solución: 

Para este caso, haremos lo mismo que en el primer ejercicio, y es que es mejor empezar a analizar nuestros datos para así poder entrarle al problema, así que iniciemos.

\displaystyle {{P}_{1}} = 1 atm

\displaystyle {{V}_{1}} = 300 ml

\displaystyle {{T}_{1}} = 35° + 273 = 308 K

\displaystyle {{P}_{2}} = 1.5 atm

\displaystyle {{V}_{2}} = 100 ml

\displaystyle {{T}_{2}} = ?

Ahora proseguimos a usar nuestra formula de la ley general del estado gaseoso

\displaystyle \frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}

Despejando la variable \displaystyle {{T}_{2}}

\displaystyle {{T}_{2}}=\frac{{{P}_{2}}{{V}_{2}}{{T}_{1}}}{{{P}_{1}}{{V}_{1}}}

Sustituimos nuestros datos

\displaystyle {{T}_{2}}=\frac{(1.5atm)(100ml)(308K)}{(1atm)(300ml)}=154K

Pero OJO! aquí no ha terminado el problema, ya que nos pide el valor de la temperatura final pero expresada en grados celcius -> °C

\displaystyle {{T}_{2}}=154K-273

\displaystyle {{T}_{2}}=-119{}^\circ C

Por lo que la temperatura final, disminuye drásticamente a una cantidad mínima, lo que sería una escala muy pero muy baja.

….Fin….

¿Dudas?

📃 Ejercicios para Practicar la Ley General del Estado Gaseoso

A continuación se muestran algunos ejemplos resueltos paso a paso, donde podrá corroborar sus resultados con la solución: 😊👇

Problema 3.- Calcular el volumen que ocupará un gas en condiciones normales, si a una presión de 940 mm de Hg y 23°C  su volumen es de 184 cm³ 

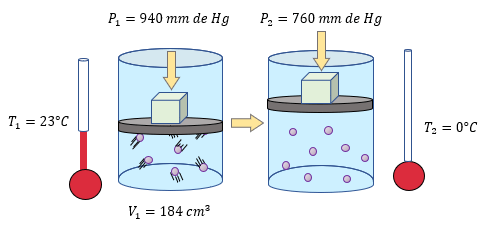
Problema de la ley general del estado gaseoso

👉 Ver Solución

Problema 4.- Una masa de hidrógeno gaseoso ocupa un volumen de 0.7 litros a una temperatura de 28 °C y a una presión absoluta de 850 mm de Hg. ¿Cuál será su presión absoluta si su temperatura aumenta a 98°C y su volumen es de 1.6 litros? 

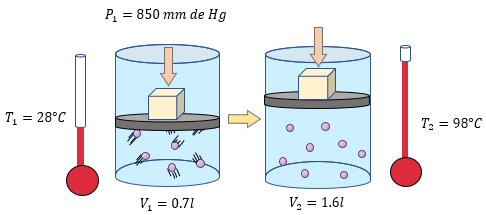
Ley general del estado gaseoso

👉 Ver Solución

Problema 5.- A un gas que está dentro de un recipiente de 4 litros se le aplica una presión absoluta de 1020 mm de Hg, y su temperatura es de 12°C. ¿Cuál será su temperatura si ahora recibe una presión absoluta de 920 mm de Hg y su volumen es de 3.67 litros

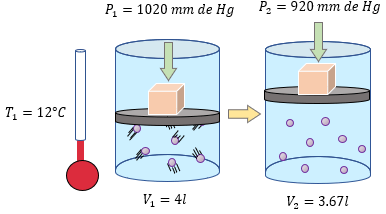
Ley general del estado gaseoso problemas

👉 Ver Solución