Ley de Charles - Ejercicios Resueltos

Hoy hablaremos sobre la Ley de Charles, una de las leyes que nos explica como los gases tienden a expandirse cuando se calientan, este gran tema que posiblemente estés viendo en alguna asignatura de física o química, en especial las leyes de los gases tal como la ley de Boyle - Mariotte, o la Ley de Gay - Lussac, sea cual sea donde lo estés viendo, hoy te llevarás un poco de información y algunos detalles importantes para resolver estos problemas y entender de que se trata.

Por cierto esta ley también es conocida como la Ley de Volúmenes Constantes, y fue formulada por el gran físico francés Jacques Charles en el siglo XVIII.

¿Qué es la Ley de Charles?

Si bien la Ley de Charles es una ley que nos indica la relación que existe entre el volumen y la temperatura, (tomar en cuenta esto), nos da a conocer un simple y sencillo razonamiento, que nos parecerá obvio.

Si nosotros ponemos un recipiente con gas en una estufa, y a ese recipiente lo sometemos a cierta temperatura, ¿Qué pasará con el recipiente con gas?, ¿Sufrirá algún cambio?, pues bien, para darle respuesta a esto es muy importante saber que la Ley de Charles, nos dice lo siguiente:

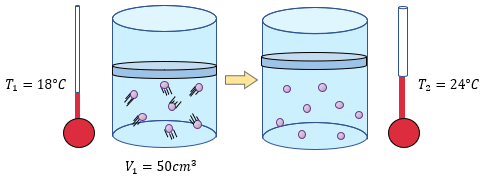
Al someter cierta masa de gas a presión constante y la temperatura en aumento, el volumen aumentará, y al disminuir la temperatura, también el volumen disminuirá.

Lo he colocado así, para que se entienda lo que el autor intenta explicar, ahora intentemos enfocarnos en la fórmula.

$\displaystyle \frac{{{P}_{1}}\cdot {{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}\cdot {{V}_{2}}}{{{T}_{2}}}$

Si la presión es constante entonces de la ley general en estado gaseoso tendrá el siguiente cambio:

$\displaystyle \frac{{{V}_{1}}}{{{T}_{1}}}=\frac{{{V}_{2}}}{{{T}_{2}}}$

Dónde:

T1 = Temperatura inicial

T2 = Temperatura final

V1 = Volumen inicial

V2 = Volumen final

¡Muy importante! La temperatura la vamos a medir en $\displaystyle \left[ {}^\circ K \right]$ grados Kelvin

Aplicaciones de la Ley de Charles

En la vida real algunas de las aplicaciones de la ley de Charles, son las siguientes:

1. Globos Aerostáticos: El principio detrás del funcionamiento de los globos aerostáticos se basa en la expansión del aire caliente dentro del globo, que aumenta su volumen y reduce su densidad, permitiendo que el globo se eleve.
2. Motores térmicos: La Ley de Charles se aplica en la expansión de gases en ciclos termodinámicos como el ciclo Otto, utilizado en motores de combustión interna.
3. Medición de temperaturas extremas: La relación entre el volumen y la temperatura se utiliza en instrumentos como los termómetros de gas.

Fórmula de la Ley de Charles

En resumen, la fórmula que utilizaremos para resolver problemas de la ley de Charles, será entonces:

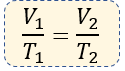
El volumen puede estar expresado en centímetros cúbicos, metros cúbicos e incluso litros. Depende del autor del problema. A diferencia de la temperatura que siempre debe ser expresada de forma absoluta, es decir en grados Kelvin.

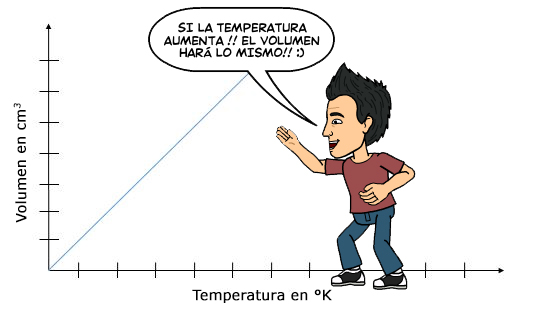
Ley de Charles Gráfica

La gráfica es muy importante para entender este tema, porque si vemos la gráfica se forma de manera proporcional, esto quiere decir lo de la imagen, a mayor temperatura, mayor volumen tendremos. ?

Ley de Charles Ejemplos

Análisis: Si nos dice, que es un gas sometido a presión constante, entonces estamos hablando de la Ley de Charles, para esa ley necesitamos dos cosas fundamentales, que serán nuestros datos, que son temperaturas y volúmenes.

Datos: 

V1: El volumen inicial nos dice que son de $ \displaystyle 23c{{m}^{3}}$

T1: La temperatura inicial es de 69°C

T2: La temperatura final es de 13°C

Solución: 

Para dar inicio a este problema, nos damos cuenta que lo que nos hace falta es el volumen final, o V2, para poder llegar a ello, solamente tenemos que despejar de la fórmula original y ver lo que obtenemos:

$\displaystyle {{V}_{2}}=\frac{{{V}_{1}}\cdot {{T}_{2}}}{{{T}_{1}}}$

y aquí algo totalmente importante, y que coloqué de rojo texto atrás, Los problemas de Charles se trabajan en escala absoluta, es decir la temperatura debe estar en grados Kelvin, para ello no es gran ciencia, solo debemos sumar 273 a las temperaturas que tenemos en grados Celcius también conocido como centígrados, quedando de la siguiente forma,

$ \displaystyle {{T}_{1}}=69+273=342{}^\circ K$

$\displaystyle {{T}_{2}}=13+273=286{}^\circ K$

Ahora solo nos queda reemplazar en la fórmula de la ley de charles , quedando lo siguiente:

$\displaystyle {{V}_{2}}=\frac{{{V}_{1}}\cdot {{T}_{2}}}{{{T}_{1}}}=\frac{(23c{{m}^{3}})(286{}^\circ K)}{342{}^\circ K}=19.23c{{m}^{3}}$

Ahora podemos analizar, que mientras la temperatura baje, el volumen disminuirá.

Solución:

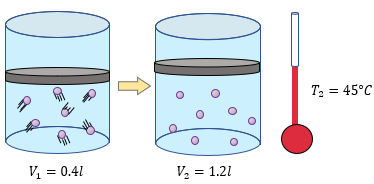
Analizamos el problema y lo que hacemos primero es reunir nuestros datos:

$\displaystyle {{V}_{1}}=$ 2.5 litros

$\displaystyle {{T}_{1}}=$ 50°C + 273 = 323°K

$\displaystyle {{V}_{2}}=$ ?

$\displaystyle {{T}_{2}}=$ 25°C + 273 = 298 °K

Sabiendo nuestra fórmula

$\displaystyle \frac{{{V}_{1}}}{{{T}_{1}}}=\frac{{{V}_{2}}}{{{T}_{2}}}$

despejamos $ \displaystyle {{V}_{2}}$

$\displaystyle {{V}_{2}}=\frac{{{V}_{1}}{{T}_{2}}}{{{T}_{1}}}$

Reemplazando nuestros datos en la fórmula.

$\displaystyle {{V}_{2}}=\frac{(2.5l)(298{}^\circ K)}{323{}^\circ K}=\frac{745}{323}l=2.306l$

Por lo que podemos observar que el volumen final será de 2.306 litros, esto afirma nuevamente que mientras la temperatura disminuya, el volumen disminuirá.

Haciendo un resumen, debes considerar lo siguiente para enfrentar a problemas de las leyes de charles  .

Análisis: Dado que la presión es constante, se aplica la Ley de Charles, donde los datos involucrados son temperaturas y volúmenes. Nuestro objetivo es calcular el volumen final, $ \displaystyle {{V}_{2}}$.

Datos:

$\displaystyle {{V}_{1}}=0.85l$

$\displaystyle {{T}_{1}}=40°C+273=313{}^\circ K$

$\displaystyle {{T}_{2}}=5°C+273=278{}^\circ K$

$\displaystyle {{V}_{2}}=?$

Solución: Usamos la fórmula de la Ley de Charles y despejamos $\displaystyle {{V}_{2}}$:

$\displaystyle V2=\frac{{V1\cdot T2}}{{T1}}$

Sustituyendo los datos:

$\displaystyle {{V}_{2}}=\frac{(0.85l)(278{}^\circ K)}{313{}^\circ K}=\frac{236.3}{313}l=0.755l$

El volumen final de la burbuja será de 0.755 litros. Observamos que al disminuir la temperatura, el volumen también disminuye, como lo predice la Ley de Charles.

Análisis: Al trabajar con temperaturas y volúmenes a presión constante, aplicamos la Ley de Charles. En este caso, calcularemos el volumen final, $\displaystyle {{V}_{2}}$.

Datos:

$\displaystyle {{V}_{1}}=12.5cm³$

$\displaystyle {{T}_{1}}=120°C+273=393{}^\circ K$

$\displaystyle {{T}_{2}}=-15°C+273=258{}^\circ K$

$\displaystyle {{V}_{2}}=?$

Solución:

Utilizamos la fórmula de la Ley de Charles:

$\displaystyle V2=\frac{{V1\cdot T2}}{{T1}}$

Sustituyendo los valores:

$\displaystyle {{V}_{2}}=\frac{(12.5cm³)(258{}^\circ K)}{393{}^\circ K}=\frac{3225}{393}cm³=8.21cm³$

El volumen final será de 8.21 cm³, confirmando que, al enfriarse el gas, su volumen disminuye proporcionalmente.

Análisis: Aplicamos la Ley de Charles para determinar el nuevo volumen, $\displaystyle {{V}_{2}}$.

Datos:

$\displaystyle {{V}_{1}}=3.8l$

$\displaystyle {{T}_{1}}=15°C+273=288{}^\circ K$

$\displaystyle {{T}_{2}}=150°C+273=423{}^\circ K$

$\displaystyle {{V}_{2}}=?$

Solución: Aplicamos la fórmula:

$\displaystyle V2=\frac{{V1\cdot T2}}{{T1}}$

Sustituyendo:

$\displaystyle {{V}_{2}}=\frac{(3.8l)(423{}^\circ K)}{288{}^\circ K}=\frac{1607.4}{288}l=5.58l$

El volumen final será de 5.58 litros, lo que indica que, al aumentar la temperatura, el volumen del gas también aumenta.

Análisis: El problema nos pide calcular la temperatura final ($\displaystyle T2$​), utilizando la Ley de Charles, ya que involucra temperatura y volumen a presión constante.

Datos:

$\displaystyle V1=5.2l$
$\displaystyle T1={{300}^{{}^\circ }}C+273={{573}^{{}^\circ }}K$
$\displaystyle V2=8.4l$
$\displaystyle T2=?$

Solución: Partimos de la fórmula de la Ley de Charles:

$\displaystyle \frac{{V1}}{{T1}}=\frac{{V2}}{{T2}}$

Despejamos $\displaystyle T2$

$\displaystyle T2=\frac{{V2\cdot T1}}{{V1}}$

Sustituimos los valores:

$\displaystyle {{T}_{2}}=\frac{{(8.4l)({{{573}}^{{}^\circ }}K)}}{{5.2l}}=\frac{{4813.2}}{{5.2}}={{925.6}^{{}^\circ }}K$

Convertimos a grados Celsius:

$\displaystyle {{T}_{2}}=925.6-273=652.6{}^\circ C$

Resultado: La temperatura final será de 652.6°C.

Análisis: En este caso, necesitamos determinar $\displaystyle V1$​ utilizando la Ley de Charles.

Datos:

$\displaystyle V2=9.375l$
$\displaystyle T2={{250}^{{}^\circ }}K$
$\displaystyle T1={{400}^{{}^\circ }}K$
$\displaystyle V1=?$

Solución: Partimos de la fórmula de la Ley de Charles:

$\displaystyle \frac{{V1}}{{T1}}=\frac{{V2}}{{T2}}$

Despejamos $\displaystyle V1$

$\displaystyle V1=\frac{{V2\cdot T1}}{{T2}}$

Sustituimos los valores:

$\displaystyle {{V}_{1}}=\frac{{(9.375l)({{{400}}^{{}^\circ }}K)}}{{{{{250}}^{{}^\circ }}K}}=\frac{{3750}}{{250}}=15l$

Resultado: El volumen inicial era de 15 litros.

Análisis: Este problema requiere verificar si la presión se mantiene constante, comprobando si los datos cumplen la Ley de Charles.

Datos:

$\displaystyle V1=7{{m}^{3}}$
$\displaystyle T1={{90}^{{}^\circ }}C+273={{363}^{{}^\circ }}K$
$\displaystyle V2=9{{m}^{3}}$
$\displaystyle T2={{200}^{{}^\circ }}C+273={{473}^{{}^\circ }}K$

Solución: La Ley de Charles establece:

$\displaystyle \frac{{V1}}{{T1}}=\frac{{V2}}{{T2}}$

Calculamos:

$\displaystyle \frac{{V1}}{{T1}}=\frac{7}{{363}}=0.01929$

$\displaystyle \frac{{V2}}{{T2}}=\frac{9}{{473}}=0.01902$

Conclusión: Dado que $\displaystyle \frac{{V1}}{{T1}}\ne \frac{{V2}}{{T2}}$, la presión no se mantuvo constante. Algún otro factor, como un cambio en la presión, intervino en el sistema.

Limitaciones

La Ley de Charles es válida solo para gases ideales y a temperaturas alejadas del punto de licuefacción del gas.

En condiciones reales, los gases pueden no comportarse idealmente debido a interacciones moleculares.

Ejercicios para Practicar de la Ley de Charles

Veamos algunos ejercicios resueltos de la Ley de Charles

A continuación se muestran algunos ejercicios adicionales de La ley de Charles para reforzar el aprendizaje de éste tema, así mismo se incluyen las soluciones paso a paso, para poder ver las soluciones debe dar click en el texto “Ver Solución”. ??

Ver Solución

Ver Solución

Ver Solución

Ver Solución

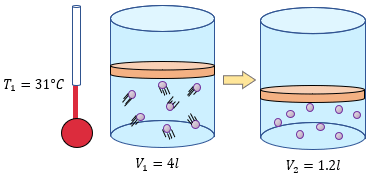
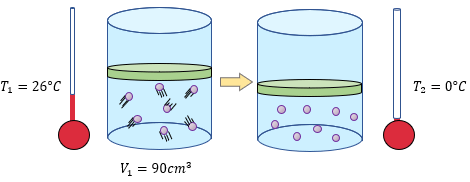
Examen de la Ley de Charles

Ahora es momento de poner en marcha tus conocimientos teórico-prácticos sobre la Ley de Charles. ¿Estás listo?