Ley de los gases ideales - Ejercicios Resueltos
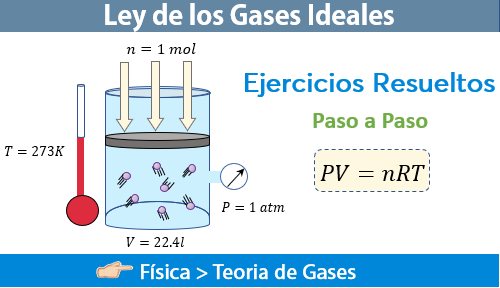
Una vez comprendido los temas de las leyes de los gases, tales como la ley de Boyle - Mariotte, la Ley de Charles, la ley de Gay - Lussac, y finalmente la ley general del estado gaseoso. Es importante conocer también la ley de los gases ideales, porque son fundamentales para entender por completo la teoría general de los gases, un tema de gran relevancia en la termodinámica y estudios de química.
? ¿Qué es un gas ideal?
Para poder comprender completamente el tema del gas ideal o gas perfecto, debemos prestar atención a lo siguiente, un gas ideal o perfecto realmente no existe, es un gas hipotético cuyo compartimiento de las variables de presión, volumen y temperatura se pueden describir completamente por la ecuación del gas ideal. Dicha ecuación especifica la relación entre las cantidades de P, V, T y n.
Las moléculas que componen a un gas ideal no se suelen atraer o repeler entre si, y su volumen es despreciable en comparación con el volumen del recipiente que lo contiene. Aunque en nuestra naturaleza no exista el caso de un gas ideal, las diferencias entre el comportamiento de un gas real en márgenes de temperatura y presión no alteran sustancialmente los cálculos, por lo que podemos hacer uso de la ecuación con toda la seguridad, para resolver diversos ejercicios de gases.
? Constante Universal de los Gases
En nuestro estudio de las leyes de los gases, hemos visto la relación de la temperatura, presión y volumen. Tal como se muestra en la siguiente fórmula de la ley general de los gases:
$\displaystyle \frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}$
Podríamos decir que la igualdad es igual a una constante en general, que la vamos a llamar "K".
$\displaystyle \frac{PV}{T}=K$
Si movemos a "T" para que pase a multiplicar a "K", la ecuación quedaría:
$\displaystyle PV=KT$
El valor de "K" lo vamos a relacionar en función del número de moles (n) de cualquier gas, esto tiene por ecuación la siguiente fórmula:
$\displaystyle K=nR$
Si sustituimos la K = nR en la ecuación que tenemos de Presión por Volumen, vamos a dar con la siguiente fórmula:
$\displaystyle PV=nRT$
Dónde:
P = Presión absoluta a la que se encuentra el gas
V = Volumen ocupado por el gas
n = Número de moles del gas que se calcula dividiendo su masa entre su peso molecular:
$\displaystyle n=\frac{m}{PM}$
R = Es la constante universal de los gases y su valor depende de las unidades usadas para su cálculo.
[alert-warning]La ecuación de la ley de los gases ideales es una de las ecuaciones más utilizadas en fisicoquímica, pues nos permite realizar varios cálculos conociendo el valor de R, ya que establece una relación entre la presión, el volumen, la temperatura y número de moles de un gas[/alert-warning]
? Ecuación de la ley de los gases ideales
En conclusión, la fórmula que vamos a emplear para la ley de los gases ideales o gases perfectos es la siguiente:
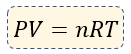
En algunos libros, hay autores que manejan esta fórmula como la Ecuación de Clapeyron
? ¿Cómo se obtiene R de la ley de los gases ideales?
Para que podamos calcular el valor de R , tenemos que considerar que un mol de cualquier gas ideal y en condiciones normales de temperatura y presión, es decir a una atmósfera y 273 K, ocupa un volumen de 22.413 litros.
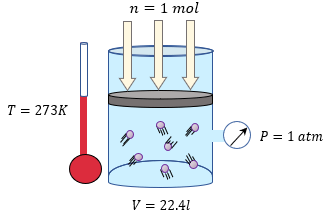
Por lo tanto, al despejar R de la ecuación anterior, tenemos:
$\displaystyle R=\frac{PV}{nT}=\frac{\left( 1atm \right)\left( 22.413l \right)}{\left( 1mol \right)\left( 273K \right)}=0.0821\frac{atm\cdot l}{mol\cdot K}$
Qué también es equivalente a:
R = 8.32 J/mol K
Para entender a fondo esta ley, veamos algunos ejercicios resueltos de la ley de los gases ideales o gases perfectos.
⭐ Ejercicios Resueltos de la Ley de los gases ideales
Vamos a comprender mejor el tema, con algunos ejercicios propuesto. Comencemos ??
Solución:
Si leemos el problema nuevamente, vemos que nos proporcionan datos como el volumen, la presión y la temperatura. Y nos pide calcular los moles de hidrógeno,es decir el valor de "n", después nos pide convertir esa cantidad de moles a unidades de masa, por lo que el problema es muy sencillo. Recordemos la fórmula:
Datos:
$\displaystyle V=230l$
$\displaystyle P=1.5atm$
$\displaystyle T=35{}^\circ C+273=308K$
Nota: Observe que hemos convertido los grados celcius a la escala absoluta de Kelvin, sumando 273.
a) Obtener los número de moles de la masa de hidrógeno gaseoso
Veamos la ecuación de la ley de los gases ideales, de la fórmula:
$\displaystyle PV=nRT$
Despejamos a "n", y tenemos:
$\displaystyle n=\frac{PV}{RT}$
Ahora si podemos sustituir nuestros datos
$\displaystyle n=\frac{PV}{RT}=\frac{\left( 1.5atm \right)\left( 230l \right)}{\left( 0.0821\frac{atm\cdot l}{mol\cdot K} \right)\left( 308K \right)}=\frac{345atm\cdot l}{25.29\frac{atm\cdot l}{mol}}=13.64mol$
Por lo que la cantidad de número de moles es de 13.64 moles
b) Convertir en masa el número de moles
Al ser hidrógeno gaseoso nos referimos a que su peso atómico o masa molar es una molécula diatómica, compuesta por dos átomos de hidrógeno
$\displaystyle {{H}_{2}}$
Y que su peso molecular (PM) es igual a 2 g/mol (porque es diatómica), entonces tenemos:
$\displaystyle m=n\left( PM \right)=\left( 13.64mol \right)\left( 2\frac{g}{mol} \right)=27.28g$
Es decir que tenemos una masa de 27.28 gramos
Solución:
El problema es muy sencillo nuevamente de resolver, si volvemos a leer nos damos cuenta que tenemos los datos del número de moles de la sustancia, un volumen y una temperatura. También sabemos el valor de nuestra constante de gases ideales. Ahora es momento de colocar nuestros datos:
Datos:
$\displaystyle R=0.0821\frac{atm\cdot l}{mol\cdot K}$
$\displaystyle n=2.35mol$
$\displaystyle V=5.92l$
$\displaystyle T=71.5{}^\circ C+273=344.5K$
a) Obteniendo la presión ejercida por el gas
De nuestra ecuación de los gases ideales
$\displaystyle \begin{array}{l}PV=nRT\\m=n\left( PM \right)\end{array}$
Despejamos a la presión:
$\displaystyle P=\frac{nRT}{V}$
Sustituimos nuestros datos en la fórmula:
$\displaystyle P=\frac{nRT}{V}=\frac{\left( 2.35mol \right)\left( 0.0821\frac{atm\cdot l}{mol\cdot K} \right)\left( 344.5K \right)}{5.92l}=11.23atm$
Por lo que la presión es de 11.23 atmósferas
? Ejercicios para practicar de la ley de los gases ideales
[alert-note] Problema 3.- Se coloca 160 gramos de oxígeno a 27°C en un recipiente con capacidad de 5 litros. Considerando que el oxígeno se comporta como un gas perfecto. ¿Cuál es el valor de la presión ejercida por la sustancia? [/alert-note]
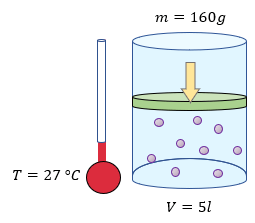
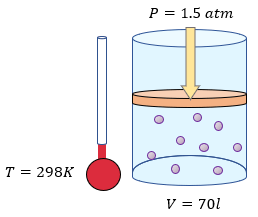
[alert-note] Problema 4.- Una masa de oxígeno gaseoso ocupa un volumen de 70 litros en un recipiente que se encuentra a una presión de 1.5 atmósferas y a una temperatura de 298K. Determinar: a) cuántos moles de oxígeno tiene. [/alert-note]
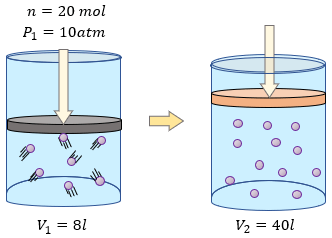
[alert-note] Problema 5.- En un laboratorio, hay una cantidad de 20 mols de un gas perfecto que sufre expansión isotérmica. La presión inicial de esta masa de gas es de 10 atm y el volumen, 8 L. Al final de la expansión, el volumen es de 40 L. Por lo tanto, determine. a) La presión final de la masa de gas, b) la temperatura que se produce en la transformación [/alert-note]
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Buenas noches ayúdeme xfis con este ejercicio:
- Una masa de gas ocupa un volumen de 1m3 a 25°C y 775 mm Hg, se comprime dentro de un tanque de 4 litros de capacidad a la presión de 6 atm. Calcular la temperatura final de gas. -
Excelente explicación, me ayudó mucho
-
Tengo una operación qué nos dejaron de tarea, y quisiera dejar un ejemplo para ver si me pueden ayudar, es así: En un tanque existe cierta cantidad de oxígeno, el cual ocupa 6.3L a 60°C y 600mmHg de presión. Averiguar a) Su volumen en condiciones normales, b)el número de moles, c)La cantidad en gramos de oxígeno
-
Jss
-
-
Buenas tardes será que me podrían ayudar con este ejercicio por favor, gracias
Una Cantidad 85,5 Kg NO de gas ideal ocupa un Volumen 2,5 a una temperatura 82°c y una presión p1 que se debe calcular, a partir de la ecuación de gases ideales. ¿Cual es la presion que se requiere para Comprimir 1/2 Volume del gas V2 Contenedor a 200°C? -
Esta pagina me ayudo muchísimo cuando no entendía la clase del profesor.
MUCHAS GRACIAS FISIMAT
36 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar