Solución Problema 1 Movimiento Parabólico

Vamos a resolver el ejercicio propuesto para reforzar los conocimientos adquiridos del Movimiento Parabólico o Tiro Parabólico , donde el estudiante pueda corroborar su respuesta y verificar si ha llegado al mismo resultado.

Nivel de Dificultad: ⭐⭐

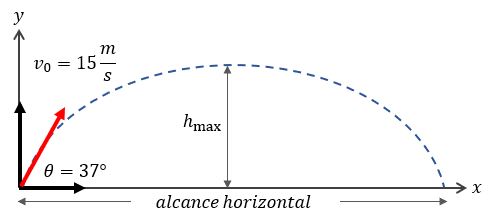
Solución:

En este ejercicio, nos piden encontrar tres puntos muy interesantes del problema:

• Tiempo que dura la pelota en el aire
• La altura máxima alcanzada
• El alcance horizontal

Datos:

$latex \displaystyle {{v}_{0}}=15\frac{m}{s}$

$latex \displaystyle \theta =37$

Si regresamos a nuestro tema principal del movimiento parabólico podremos revisar las fórmulas y seleccionar las que mejor se acomoden a nuestro ejemplo. Comencemos entonces por resolver el problema 😀

a) Obteniendo el tiempo que dura la pelota en el aire

Vamos a utilizar la siguiente fórmula:

$latex \displaystyle {{T}_{t}}=\frac{2{{v}_{0}}sen\theta }{g}$

Si sustituimos nuestros datos

$latex \displaystyle {{T}_{t}}=\frac{2{{v}_{0}}sen\theta }{g}=\frac{2\left( 15\frac{m}{s} \right)sen37{}^\circ }{9.8\frac{m}{{{s}^{2}}}}=1.84s$

Obtenemos un total de 1.84 segundos que dura la pelota en el aire.

b) Obteniendo la altura máxima alcanzada

Para obtener la altura máxima alcanzada, vamos a utilizar la siguiente fórmula:

$latex \displaystyle {{h}_{\max }}=\frac{{{v}_{0}}^{2}se{{n}^{2}}\theta }{2g}$

Nuevamente, sustituimos nuestros datos en la fórmula y obtenemos:

$latex \displaystyle {{h}_{\max }}=\frac{{{v}_{0}}^{2}se{{n}^{2}}\theta }{2g}=\frac{{{(15\frac{m}{s})}^{2}}{{\left( sen37{}^\circ \right)}^{2}}}{2(9.8\frac{m}{{{s}^{2}}})}=4.157m$

Con esto se obtiene una altura máxima alcanzada de 4.157 metros.

c) Obteniendo el alcance horizontal

En el caso del alcance horizontal, debemos recurrir a la siguiente fórmula:

$latex \displaystyle x={{v}_{0x}}t$

Para conocer la velocidad que se genera en el eje "x", debemos multiplicar el valor del vector velocidad por el coseno del ángulo de 37°, de esta forma:

$latex \displaystyle {{v}_{0x}}={{v}_{o}}\cos 37{}^\circ =(15\frac{m}{s})\cos 37{}^\circ =11.98\frac{m}{s}$

Ahora si podemos aplicar la fórmula del alcance horizontal, y esto nos daría:

$latex \displaystyle x={{v}_{0x}}t=\left( 11.98\frac{m}{s} \right)(1.84s)=22.04m$

Es decir, un alcance horizontal de 22.04 metros

Resultados:

$latex \displaystyle \begin{array}{l}{{T}_{t}}=1.84s\\{{h}_{\max }}=4.157m\\x=22.04m\end{array}$