Movimiento Parabólico - Ejercicios Resueltos

¿Cómo están Lectores 😎 ?, hoy tenemos un nuevo artículo que habla exclusivamente sobre el tiro parabólico o movimiento parabólico, uno de los temas más importantes dentro de la cinemática y un claro ejemplo de la trayectoria del movimiento de un cuerpo en dos dimensiones, o bien sobre algún plano.

Estaremos hablando sobre un término muy común en física que es sobre los proyectiles, y de aquí podemos formular la siguiente pregunta ¿qué es un proyectil?.

Un proyectil es un cuerpo que inicialmente  se le impulsa una velocidad inicial  por dicho efecto mantiene una trayectoria parabólica determinada causada por la aceleración de la gravedad y la resistencia del aire. Si queremos citar un ejemplo, puede ser un niño pateando un balón, o un objeto siendo tirado por alguna persona, es importante recordar que a diferencia de la caída libre, en la caída libre la velocidad inicial es cero, y en el movimiento parabólico hay existencia de una velocidad inicial. 😀

Si bien, la definición o concepto del tiro parabólico es entender que  es la combinación de dos movimientos independientes , el primero es un MRUA (movimiento rectilíneo uniformemente acelerado) que se expresa de alguna forma en un tiro vertical durante la elevación y como caída libre durante su caída. El segundo se trata de un MRU (Movimiento rectilíneo uniforme) característica por la cual permanece el movimiento constante durante todo el recorrido. ¿Se entiende?, esperamos que si 😀

Fórmulas del Movimiento Parabólico

Antes de establecer las fórmulas del movimiento parabólico, primero analicemos la siguiente imagen que describe un claro ejemplo de dicho movimiento en dos dimensiones.

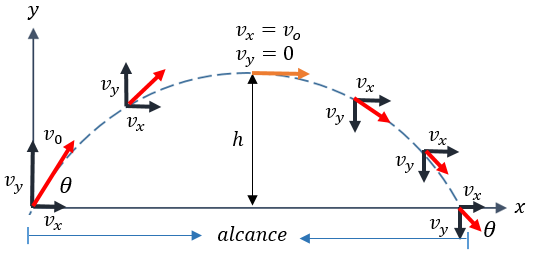
Es importante tener en cuenta la interpretación gráfica para que no haya problema alguno con los ejemplos del movimiento parabólico, entonces lo primero que observamos en la descripción del movimiento, es lo siguiente.

1. El vector de velocidad inicial se descompone en sus componentes rectangulares horizontal (vx) y vertical (vy)
2.  Durante el movimiento ascendente, la componente vertical de la velocidad empieza a disminuir.
3.  Llegando a la altura máxima, la componente vertical disminuye hasta llegar a cero.
4. Después de ascender el cuerpo, la componente vertical empieza aumentar nuevamente.
5. La componente horizontal, se mantiene constante durante todo el movimiento.

Ahora bien, las fórmulas que vamos a usar en este movimiento oblicuo parabólico, es el siguiente:

1.- Para calcular la altura máxima, aplicamos:

$\displaystyle h=\frac{{{v}_{0}}^{2}se{{n}^{2}}\theta }{2g}$

2.- Para calcular el alcance , aplicamos:

$\displaystyle R=\frac{{{v}_{0}}^{2}sen2\theta }{g}$

3.- Para calcular el tiempo total, aplicamos:

$\displaystyle {{t}_{t}}=\frac{2{{v}_{0}}sen\theta }{g}$

4.- Para calcular la posición de un proyectil en un determinado tiempo

Para x es :

$\displaystyle x={{v}_{0x}}t$

Para y es:

$\displaystyle y={{v}_{0y}}t-\frac{1}{2}g{{t}^{2}}$

5.- Para calcular el tiempo en la altura máxima es:

$\displaystyle t'=\frac{{{v}_{0y}}}{g}$

Ahora es momento de pasar a los ejercicios resueltos del tiro parabólico.

6.- Para descomponer la forma rectangular del vector velocidad es:

$\displaystyle \begin{array}{l}{{v}_{0x}}={{v}_{0}}\cos \theta \\{{v}_{0y}}={{v}_{0}}sen\theta \end{array}$

7.- Para obtener la magnitud de la velocidad en un determinado punto es:

$\displaystyle v=\sqrt{{{\left( {{v}_{0x}} \right)}^{2}}+{{\left( {{v}_{0y}} \right)}^{2}}}$

8.- Para obtener la velocidad en "y" en un determinado tiempo.

$\displaystyle {{v}_{y}}={{v}_{0y}}-gt$

Con esto tenemos para poder resolver nuestros primeros ejemplos.

9.- Para calcular el alcance teniendo el tiempo total y velocidad en "x".

$\displaystyle x={{v}_{0x}}{{t}_{t}}$

Ejercicios Resueltos del Movimiento Parabólico

Veamos la gráfica del problema:

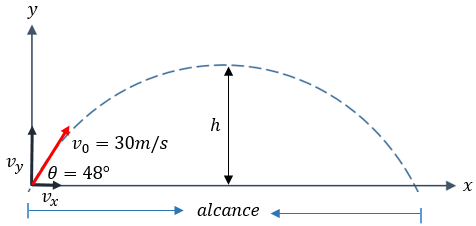
Solución: Empecemos a resolver los incisos de éste ejemplo.

A) Para calcular nuestra altura, apliquemos la fórmula 1 que pusimos arriba.

$\displaystyle h=\frac{{{v}_{0}}^{2}se{{n}^{2}}\theta }{2g}=\frac{{{(30\frac{m}{s})}^{2}}se{{n}^{2}}(48{}^\circ )}{2(9.8\frac{m}{{{s}^{2}}})}=25.36m$

Para el seno al cuadrado de 48°, primero se obtiene el seno de 48 y luego al resultado se eleva al cuadrado, y se realizan las operaciones indicadas.

B) Para calcular el alcance, apliquemos la fórmula 2, así que tendremos lo siguiente:

$\displaystyle R=\frac{{{v}_{0}}^{2}sen2\theta }{g}=\frac{{{(30\frac{m}{s})}^{2}}sen2(48{}^\circ )}{9.8\frac{m}{{{s}^{2}}}}=91.33m$

Para el angulo doble del seno, el ángulo de 48° se multiplica por dos, después se le saca el seno a ese resultado y finalmente se realizan las operaciones.

C) Para calcular el tiempo que permanece el objeto sobre el aire, aplicamos la fórmula 3.-

$\displaystyle {{t}_{t}}=\frac{2{{v}_{0}}sen\theta }{g}=\frac{2(30\frac{m}{s})sen(48{}^\circ )}{9.8\frac{m}{{{s}^{2}}}}=4.55s$

Y con esto prácticamente habremos resuelto nuestro primer ejercicio ¿fácil no? , realmente hemos aplicado las fórmulas 😎

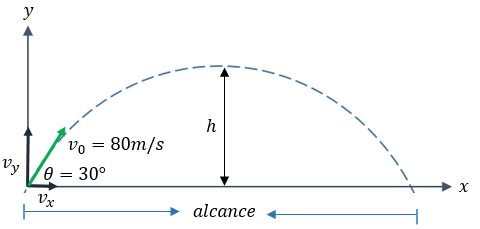
Solución: Empecemos a resolver los incisos de éste ejemplo.

A) Para calcular la posición y velocidad en los 6 segundos, aplicaremos la fórmula 4, pero primero debemos descomponer en su forma rectangular a nuestro vector de velocidad inicial, con la fórmula 6.-

$\displaystyle {{v}_{0x}}={{v}_{0}}\cos \theta =\left( 80\frac{m}{s} \right)\cos 30{}^\circ =69.28\frac{m}{s}$

$\displaystyle {{v}_{0y}}={{v}_{0}}sen\theta =\left( 80\frac{m}{s} \right)sen30{}^\circ =40\frac{m}{s}$

Ahora si procedemos a calcular la posición a los 6 segundos.

$\displaystyle x={{v}_{0x}}t=(69.28\frac{m}{s})(6s)=415.68m$

415.68 metros es la posición en "x" a los 6 segundos.

$\displaystyle y={{v}_{0y}}t-\frac{1}{2}g{{t}^{2}}=(40\frac{m}{s})(6s)-\frac{(9.8\frac{m}{{{s}^{2}}}){{(6s)}^{2}}}{2}=240m-176.4m=63.6m$

63.6 metros es la posición en "y" a los 6 segundos.

🚀 Ahora para saber la velocidad general en ese punto aplicamos primero la fórmula 8.

$\displaystyle {{v}_{y}}={{v}_{0y}}-gt=40\frac{m}{s}-(9.8\frac{m}{{{s}^{2}}})(6s)=-18.8\frac{m}{s}$

La velocidad negativa, indica que ya pasó el punto más alto y el proyectil está empezando a descender.

Aplicando la fórmula 7, y recordando que la velocidad en "x" a los 6 segundos, es la misma siempre, no hay cambios a diferencia de "y" que si cambia, y que ya hemos calculado.

$\displaystyle v=\sqrt{{{\left( {{v}_{0x}} \right)}^{2}}+{{\left( {{v}_{0y}} \right)}^{2}}}=\sqrt{{{\left( 69.28\frac{m}{s} \right)}^{2}}+{{\left( -18.8\frac{m}{s} \right)}^{2}}}=71.79\frac{m}{s}$

B) Para que podamos calcular el tiempo en alcanzar la altura máxima, usamos la fórmula 5.-

$\displaystyle t'=\frac{{{v}_{0y}}}{g}=\frac{40\frac{m}{s}}{9.8\frac{m}{{{s}^{2}}}}=4.08s$

Qué sería el tiempo en tocar la altura máxima.

C) Para poder calcular el alcance, hacemos uso de la fórmula 9, aquí multiplicaremos el tiempo de la altura máxima por 2, para saber el tiempo total.

$\displaystyle x={{v}_{0x}}{{t}_{t}}=(69.28\frac{m}{s})(8.16s)=565.23m$

Y con esto tenemos el problema resuelto 💪

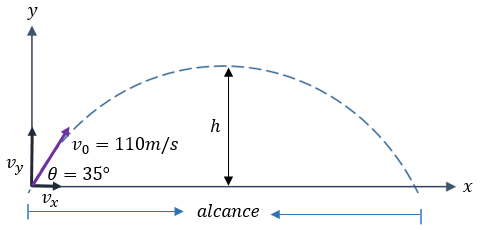
Solución: Para este tercer ejemplo, se da por hecho que ya sabemos como aplicar las fórmulas, así que solo estaremos aplicando la fórmula para obtener nuestros resultados.

A) Posición del Proyectil a los 6 segundos, pero primero descomponemos el vector velocidad.

$\displaystyle {{v}_{0x}}={{v}_{0}}\cos \theta =\left( 110\frac{m}{s} \right)\cos 35{}^\circ =90.11\frac{m}{s}$

$\displaystyle {{v}_{0y}}={{v}_{0}}sen\theta =\left( 110\frac{m}{s} \right)sen35{}^\circ =63.09\frac{m}{s}$

Ahora, si calculamos la posición, tanto en "x" como en "y":

$\displaystyle x=(90.11\frac{m}{s})(6s)=540.66m$

$\displaystyle y={{v}_{0y}}t-\frac{1}{2}g{{t}^{2}}=(63.09\frac{m}{s})(6s)-\frac{(9.8\frac{m}{{{s}^{2}}}){{(6s)}^{2}}}{2}=378.54m-176.4=202.14$

B) Para poder calcular la velocidad a los 6 segundos, solamente nos hace falta calcular la velocidad en y, ya que en "x" es la misma todo el tiempo.

$\displaystyle {{v}_{y}}={{v}_{0y}}-gt=63.09\frac{m}{s}-(9.8\frac{m}{{{s}^{2}}})(6s)=4.29\frac{m}{s}$

Ahora si calculamos la magnitud de la velocidad a los 6 segundos.

$\displaystyle v=\sqrt{{{\left( {{v}_{0x}} \right)}^{2}}+{{\left( {{v}_{0y}} \right)}^{2}}}=\sqrt{{{\left( 90.11\frac{m}{s} \right)}^{2}}+{{\left( 4.29\frac{m}{s} \right)}^{2}}}=90.21\frac{m}{s}$

C) Para calcular el tiempo en la altura máxima, aplicamos su fórmula:

$\displaystyle t'=\frac{{{v}_{0y}}}{g}=\frac{63.09\frac{m}{s}}{9.8\frac{m}{{{s}^{2}}}}=6.44s$

D) Para el tiempo total de vuelo, solo hace falta multiplicar por 2, al tiempo de la altura máxima.

$\displaystyle t''=2\left( \frac{{{v}_{0y}}}{g} \right)=2\left( 6.44s \right)=12.88s$

E) Para calcular el alcance logrado, aplicamos la fórmula:

$\displaystyle x={{v}_{0x}}{{t}_{t}}=(90.11\frac{m}{s})(12.88s)=1160.62m$

y listo, problema resueltooooo!!! 😀

📃 Ejercicios Para Practicar de Movimiento Parabólico

Resuelva los siguientes ejercicios y comprueba sus resultados con las soluciones explicadas paso a paso 😀

👉 Ver Solución 

👉 Ver Solución

🔹 Conclusión del Tiro Parabólico

Para concluir éste movimiento oblicuo, podemos decir que; el tiro parabólico es la combinación de dos movimientos, el MRU y el MRUA; o bien el tema de la caída libre o tiro vertical. Por ende sabemos también que para que se produzca un tiro parabólico debe de haber un ángulo de inclinación y cierta velocidad inicial, que después se descompone en sus componentes horizontal y vertical y se observa todo lo que ocurre con sus propiedades cinemáticas del vuelo a través de las fórmulas que ya hemos mencionado. Posee cierta diferencia al tiro horizontal, que veremos en otro artículo. ¡Gracias por leernos y aprender! 😀