Caída Libre

Hoy voy a tocar un tema de gran importancia e interés dentro de la cinemática, una de las ramas que se encarga de estudiar la física, por lo que este post será completamente un excelente artículo para aprender, conocer y así embarcarse al principio fundamental de las efectos dinámicos que esto pueda ocasionar.

🤔 ¿Qué es la caída libre?

La caída libre, es uno de los conceptos que más interés ha tenido en el estudio del movimiento de caída de los cuerpos próximos a la superficie de la tierra. Por ejemplo, el hecho de lanzar una piedra o simplemente soltarla hasta esperar que caiga sobre el suelo, hacemos un experimento básico sobre este hecho, e incluso podemos darnos cuenta del aumento de la velocidad del objeto mientras el tiempo transcurre.

Se dice entonces, que un cuerpo experimente una caída libre, si desciende sobre la superficie de la tierra y no sufre ninguna resistencia originada por el aire o cualquier otro factor o sustancia. De manera práctica, la resistencia del aire se puede despreciar ya que es tan pequeña.

Aristóteles y Galileo en la caída de los cuerpos

Dos grandes científicos de hace ya muchos años, fueron dos grandes pilares de la física que pusieron el cimiento para el desarrollo y análisis de la caída de los cuerpos, por citar: Aristóteles creía que si desde un lugar alto se lanzaba un objeto menos pesado, de poca masa contra otro objeto con características totalmente diferente, es decir, un objeto sumamente pesado, ambos caerían al mismo tiempo y recorriendo velocidades iguales, y eso se creyó durante cientos de años, ya que al ser un gran filósofo de renombre, era muy difícil poder quitar esa idea a muchas personas que seguían la doctrina aristotélica.

Pasó aproximadamente dos milenios, para que llegara el gran Galileo Galilei para darle un cambio radical a esta idea, y poder así darle un concepto analítico de otra forma, ya que Galileo es considerado el padre o creador del método experimental en física, o sea que a fuerzas es necesario tener que comprobar lo que afirmas mediante experimentos y cuidadosas observaciones para poder ser verídico.

Problema de Caída Libre

Galileo dedujo que, si se dejan caer simultáneamente dos objetos a la misma altura, uno pesado y otro ligero ambos llegarán o caerán sobre el suelo con la misma aceleración y al mismo tiempo, lo contrario a Aristóteles.

Bajo estas bases se inició el proceso para las fórmulas de caída libre, y así iniciar un estudio exhausto de esto.

⭐ Fórmulas de caída libre

Existen diversas fórmulas para el tema de caída libre, sin embargo es importante diferenciar unas de otras ya que despejando algunas variables se nos generará otra fórmula y así sucesivamente.

Considerando a la gravedad como $\displaystyle 9.8\frac{m}{{{s}^{2}}}$ Tenemos que:

$\displaystyle v={{v}_{0}}+gt$

Esta fórmula la podemos encontrar como \displaystyle v={{v}_{0}}+at, simplemente hemos remplazado la aceleración, por la \displaystyle g de gravedad, ya que la única aceleración que tendremos en caída libre, será la aceleración de la gravedad.

$\displaystyle d={{v}_{0}}t+\frac{1}{2}a{{t}^{2}}$

y finalmente tenemos otra fórmulita más.

$\displaystyle {{v}^{2}}={{v}_{0}}^{2}+2gd$

recordar que:

$\displaystyle v=$ Velocidad final

$\displaystyle {{v}_{0}}=$ Velocidad inicial

$\displaystyle t=$ Tiempo

$\displaystyle d=$ Distancia.

Ahora si, vamos a la parte más importante.

🔸 Ejercicios resueltos de caída libre

Problema 1. Un cuerpo se deja caer desde un edificio de la ciudad de México. Calcular, a) ¿Cuál será la velocidad final que este objeto tendrá a los 10 segundos cuando llegue el suelo?, b) ¿Cuál es la altura del edificio? 

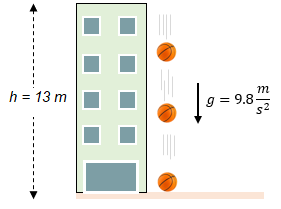
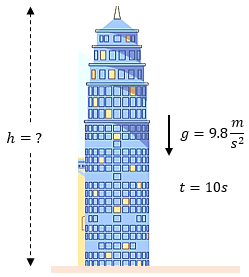
Problema de Caída Libre

Solución: 

La solución es sumamente sencilla como todos los ejemplos resueltos de caída libre, para ello vamos a considerar algunos datos que no están implícitos en el problema, como lo es la gravedad y velocidad inicial.

a) Calculando la velocidad final

Si el cuerpo se deja caer desde una altura,entonces su velocidad inicial es nula o cero, y la constante de gravedad es obviamente 9.8 m/s², por lo que:

$\displaystyle g=9.8\frac{m}{{{s}^{2}}}$

$\displaystyle {{v}_{0}}=0\frac{m}{s}$

Teniendo estos datos, veamos otros que si están implícitos en el problema, tal como lo es el tiempo. \displaystyle t=10s Ahora, veamos que fórmula nos permite reemplazar esos datos y encontrar el resultado, por lo que usaremos:

$\displaystyle v={{v}_{0}}+gt$

Reemplazando datos:

$\displaystyle v={{v}_{0}}+gt$

$\displaystyle v=0\frac{m}{s}+(9.8\frac{m}{{{s}^{2}}})(10s)$

$\displaystyle v=98\frac{m}{s}$

Por lo que la velocidad final, es de 98 m/s

b) Calculando la altura del edificio

Para poder calcular la altura del edificio, usaremos la siguiente fórmula:

$\displaystyle h={{v}_{0}}t+\frac{g{{t}^{2}}}{2}$

Como la velocidad inicial es cero, porque se trata de una caída libre, entonces la fórmula se reduce:

$\displaystyle h=\frac{g{{t}^{2}}}{2}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle h=\frac{g{{t}^{2}}}{2}=\frac{\left( 9.8\frac{m}{{{s}^{2}}} \right){{\left( 10s \right)}^{2}}}{2}=\frac{\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 100{{s}^{2}} \right)}{2}=490m$

Por lo que la altura del edificio es de 490 metros.

Problema 2. Se deja caer una pelota de básquetbol desde una altura de 90 metros. Calcular, a) El tiempo que demora en caer, b) La velocidad con la que llega al suelo

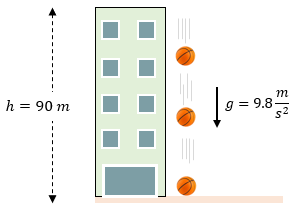
Problema de caída libre

Solución:

El problema 2, es muy similar al problema 1. Con la diferencia que lo que nos piden es el tiempo que demora en caer la pelota desde una altura de 90 metros, entonces colocamos nuestros datos:

$\displaystyle h=90m$

$\displaystyle g=9.8\frac{m}{{{s}^{2}}}$

Procedemos a realizar nuestros cálculos.

a) Calcular el tiempo que demora en caer

Emplearemos la siguiente fórmula:

$\displaystyle h={{v}_{0}}t+\frac{g{{t}^{2}}}{2}$

Como la velocidad inicial es cero, por ser caída libre, entonces la fórmula se reduce:

$\displaystyle h=\frac{g{{t}^{2}}}{2}$

Como es el tiempo lo que nos piden calcular, entonces lo despejamos de la fórmula

$\displaystyle t=\sqrt{\frac{2h}{g}}$

Ahora si podemos sustituir nuestros datos en la fórmula:

$\displaystyle t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\left( 90m \right)}{9.8\frac{m}{{{s}^{2}}}}}=\sqrt{\frac{180m}{9.8\frac{m}{{{s}^{2}}}}}=\sqrt{18.37{{s}^{2}}}=4.28s$

Es decir que la pelota de básquetbol le tomó 4.28 segundos en llegar al suelo.

b) Calcular la velocidad con la que llega al suelo

Usaremos la siguiente fórmula:

$\displaystyle {{v}_{f}}={{v}_{0}}+gt$

Recordar que al ser un problema de caída libre, la velocidad inicial es cero. Entonces nuestra fórmula se reduce a

$\displaystyle {{v}_{f}}=gt$

Ahora si, podemos sustituir nuestros datos en la fórmula:

$\displaystyle {{v}_{f}}=gt=\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 4.28s \right)=41.9\frac{m}{s}$

La velocidad a la que llega la pelota de básquetbol es de 41.9 m/s

Ahora veamos el siguiente ejemplo, que sin duda es un problema más completo, solo que este problema es un problema que implica al Tiro Vertical

 Problema 3. Un cuerpo es lanzando verticalmente hacía arriba con una velocidad inicial de 30 m/s  donde se desprecia la resistencia del aire. Conteste los siguientes incisos del problema. 

caidalibrea) ¿Cuál será la velocidad del cuerpo 2 segundos después de su lanzamiento?

b) ¿Cuánto tarda el cuerpo en llegar al punto más alto de su trayectoria?

c) ¿Cuál es la altura máxima alcanzada por el cuerpo?

d) ¿A qué velocidad regresa el cuerpo al punto de lanzamiento?

e) ¿Cuánto tardo en descender?

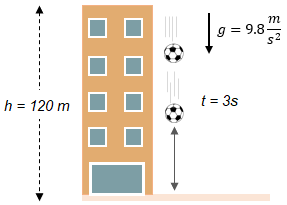
Solución:

Este problema es uno de los de caída libre muy completos, donde podemos razonar y analizar cada caso que nos podamos topar y así resolverlos sin dificultad alguna.

a) En esta parte, nos piden la velocidad del cuerpo a los 2 segundos después de su lanzamiento, ¿qué datos tenemos?, es momento de analizar los datos que se nos arroja.

$\displaystyle {{v}_{0}}=30\frac{m}{s}$

$\displaystyle g=-9.8\frac{m}{{{s}^{2}}}$

La gravedad permanecerá negativa, porque al aventar el balón hacía arriba, esta expresa un valor contrario de signo.

$\displaystyle t=2s$

Usando la siguiente fórmula, y sustituyendo, tenemos.

$\displaystyle v={{v}_{0}}+gt=30\frac{m}{s}-(9.8\frac{m}{{{s}^{2}}}\cdot 2s)=30\frac{m}{s}-19.6\frac{m}{s}=10.4\frac{m}{s}$

Por lo que la velocidad del cuerpo a los 2 segundos, sería de 10.4 m/s.

b) En este inciso nos piden encontrar el tiempo cuando el objeto logra el punto más alto de la trayectoria, y esto es muy sencillo de calcular, pero para entonces se necesita crear un análisis.

Cuando el objeto logre su velocidad en la trayectoria más alta, esa velocidad se hace cero, puesto que en ese momento empieza a descender en caída libre, por lo que tendríamos:

$\displaystyle v=0\frac{m}{s}$

$\displaystyle 0\frac{m}{s}=30\frac{m}{s}-(9.8\frac{m}{{{s}^{2}}})t$

despejamos a la variable “t”

$\displaystyle t=\frac{-30\frac{m}{s}}{-9.8\frac{m}{{{s}^{2}}}}=3.06s$

Por lo que podemos decir que justamente en 3.06 segundos, se alcanza la altura o trayectoria más alta.

c) Para este inciso nos piden la altura más alta que logra alcanzar el objeto lanzado, por lo que usaremos la siguiente fórmula:

$\displaystyle d={{v}_{0}}t+\frac{1}{2}g{{t}^{2}}$

Como sabemos del inciso b), el tiempo que logró alcanzar el objeto en la trayectoria más alta fue de 3.06 segundos, por lo que lo reemplazaremos en el valor de “t” de la fórmula anterior, quedando.

$\displaystyle d=(30\frac{m}{s})(3.06s)-\frac{1}{2}(9.8\frac{m}{{{s}^{2}}}){{(3.06s)}^{2}}$

$\displaystyle d=91.8m-45.88m=45.91m$

por lo que la altura máxima que alcanza el objeto es de 45.91 metros.

d) En esta parte nos piden encontrar la velocidad a la que regresa el cuerpo al punto de lanzamiento, pero para ello hay que pensar un poco, si el objeto fue lanzado con una velocidad inicial, pero al momento de lograr el punto máximo de altura, el cuerpo empieza a descender con una velocidad inicial de 0 m/s, por lo que nuestros datos serían:

$\displaystyle {{v}_{0}}=0\frac{m}{s}$

$\displaystyle d=45.91m$

$\displaystyle g=9.8\frac{m}{{{s}^{2}}}$

Por lo que usaremos la siguiente ecuación:

$\displaystyle {{v}^{2}}-{{v}_{0}}^{2}=2gd$

$\displaystyle {{v}^{2}}=2gd$

$\displaystyle v=\sqrt{2gd}$

Reemplazando nuestros datos:

$\displaystyle v=\sqrt{2(9.8\frac{m}{{{s}^{2}}})(45.91m)}=30\frac{m}{s}$

Por lo que podemos darnos cuenta y como era de suponer, la velocidad en el punto de partida es el mismo que el inicial 🙂

y finalmente, el último inciso

e) Cuánto tiempo tarda en descender?, el tiempo que tarda en descender totalmente se analiza desde el punto que logra la altura máxima e inicia en descenso, es decir.

$\displaystyle v={{v}_{0}}+gt$

la velocidad sería de 30 m/s, así como el tiempo sería de 3.06 segundos, entonces teniendo estos datos.

$\displaystyle 30\frac{m}{s}=0\frac{m}{s}+(9.8\frac{m}{{{s}^{2}}})t$

$\displaystyle t=\frac{30\frac{m}{s}}{9.8\frac{m}{{{s}^{2}}}}=3.06s$

Cómo podemos darnos cuenta, el tiempo de descenso es igual al tiempo de subida.

Espero, este tema haya sido de tu agrado y hayas comprendido la generalidad del tema de caída libre, cualquier duda o inquietud no dudes en comentar.

Saludos 🙂

📃 Ejercicios para Practicar de Caída Libre

Ahora es momento de resolver ejercicios de caída libre para reforzar el tema, recuerde que puede ver la solución paso a paso. 😊👇

Problema 4.- Una niña deja caer una muñeca desde una ventana que está a 80 metros de la altura sobre el suelo. Calcular, a) ¿Qué tiempo tardará en caer?, b) ¿Con qué magnitud de velocidad choca contra el suelo? 

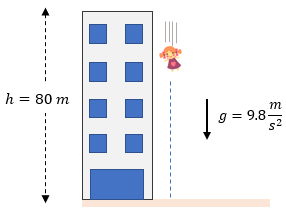
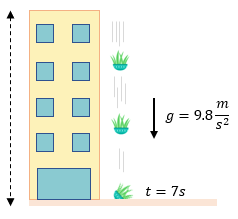
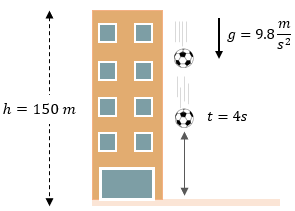
Problema de Caída Libre

👉 Ver Solución

Problema 5.- Una maceta cae desde la azotea de un edificio y tarda en llegar al suelo 7 segundos. Calcular, a) La altura del edificio, b) La magnitud de la velocidad con que choca contra el suelo.

Problema de Caída Libre

👉 Ver Solución

Problema 6.- Desde una altura de 150 metros se deja caer libremente una pelota. Calcular, a) ¿cuánto ha descendido a los 4 segundos?, b) ¿qué velocidad tiene a los 4 segundos?, c) ¿Cuánto le falta recorrer para llegar al suelo?

Problema de Caída Libre

👉 Ver Solución

✨ Más Problemas Resueltos de Caída Libre

Si deseas practicar más ejercicios o problemas sobre caída libre, te recomendamos nuestra página amiga, y ver más ejercicios para practicar.

🔥 Problemas Resueltos de Caída Libre