Solución Problema 2 Movimiento Parabólico

Para el segundo ejercicio propuesto en el reforzamiento de los conocimientos adquiridos del Movimiento Parabólico o Tiro Parabólico , es necesario tener conocimiento del despeje de fórmulas, ya que se tendrá que recurrir a ellas para encontrar las soluciones adecuadas.

Nivel de Dificultad: ⭐⭐

Solución:

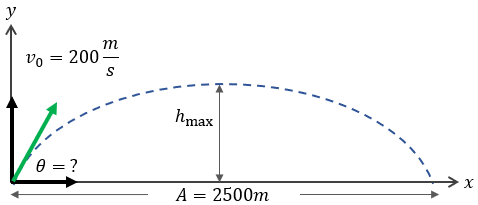
En este ejercicio solamente nos piden encontrar dos puntos importantes:

• El ángulo con el cuál debe ser lanzada la bala
• El tiempo que tarda en llegar al blanco

Datos:

$latex \displaystyle {{v}_{0}}=200\frac{m}{s}$

$latex \displaystyle A=2500m$

a) Obteniendo el ángulo

Para obtener el ángulo de la bala, es importante que nos enfoquemos en la siguiente fórmula:

$latex \displaystyle A=\frac{{{v}_{0}}^{2}sen2\theta }{g}$

Despejando a Sen 2θ

$latex \displaystyle sen2\theta =\frac{A\cdot g}{{{v}_{0}}^{2}}$

Sustituyendo los datos en la fórmula:

$latex \displaystyle sen2\theta =\frac{A\cdot g}{{{v}_{0}}^{2}}=\frac{(2500m)(9.8\frac{m}{s})}{{{(200\frac{m}{s})}^{2}}}=0.6125$

Es decir:

$latex \displaystyle sen2\theta =0.6125$

Ahora procedemos a despejar al seno como "arcoseno".

$latex \displaystyle 2\theta =arcsen(0.6125)$

$latex \displaystyle 2\theta =37.77{}^\circ $

Despejando al ángulo θ

$latex \displaystyle \theta =\frac{37.77{}^\circ }{2}=18.88{}^\circ $

Es decir que el ángulo es de 18.88° .

b) Obteniendo el tiempo que tarda en llegar al blanco

Vamos a utilizar la siguiente fórmula:

$latex \displaystyle {{T}_{t}}=\frac{2{{v}_{0}}sen\theta }{g}$

Sustituyendo los datos en la fórmula:

$latex \displaystyle {{T}_{t}}=\frac{2{{v}_{0}}sen\theta }{g}=\frac{2(200\frac{m}{s})(sen18.88{}^\circ )}{9.8\frac{m}{{{s}^{2}}}}=13.20s$

Es decir, un tiempo total de 13.20 segundos

Y con esto queda resuelto el ejercicio 😎

Resultados:

$latex \displaystyle \begin{array}{l}\theta =18.88{}^\circ \\{{T}_{t}}=13.20s\end{array}$