Solución Problema 2 del Principio de Bernoulli

De forma similar al ejemplo anterior, en este problema del Principio de Bernoulli reforzamos el concepto principal que es la utilización correcta de la fórmula, con ello se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇

Nivel de Dificultad: ⭐⭐⭐⭐⭐

Problema 4.- Calcule la velocidad del fluido en el punto A y su gasto, de un flujo volumétrico de agua a 5°C pasa por el sistema ilustrado en la imagen

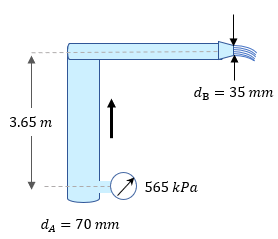
Problema del Principio de Bernoulli

Solución:

Para poder darle solución a este tipo de problema, es importante que analicemos primero la fórmula que emplearemos, es decir; observar si de alguna forma la ecuación del principio de Bernoulli tiene alguna modificación. La fórmula en principio es la siguiente:

$\displaystyle \frac{{{v}_{A}}^{2}}{2}+g{{h}_{A}}+\frac{{{p}_{A}}}{{{\rho }_{A}}}=\frac{{{v}_{B}}^{2}}{2}+g{{h}_{B}}+\frac{{{p}_{B}}}{{{\rho }_{B}}}$

La presión en el punto B está abierta a la atmósfera, por lo tanto la presión en ese punto es igual a cero. Con esto se cancela y se simplifica nuestra fórmula:

$\displaystyle \frac{{{v}_{A}}^{2}}{2}+g{{h}_{A}}+\frac{{{p}_{A}}}{{{\rho }_{A}}}=\frac{{{v}_{B}}^{2}}{2}+g{{h}_{B}}$

Nos piden encontrar la velocidad en el punto A, es decir la velocidad inicial, entonces tenemos que dejar nuestra fórmula expresada en esos términos. Realizamos el despeje correspondiente:

$\displaystyle \frac{{{v}_{A}}^{2}}{2}=\frac{{{v}_{B}}^{2}}{2}+g{{h}_{B}}-g{{h}_{A}}-\frac{{{p}_{A}}}{{{\rho }_{A}}}$

Para hacer mucho más fácil el proceso, vamos a juntar en el lado izquierdo a las velocidades A y B, puesto que no las tenemos:

$\displaystyle \frac{{{v}_{A}}^{2}}{2}-\frac{{{v}_{B}}^{2}}{2}=g{{h}_{B}}-g{{h}_{A}}-\frac{{{p}_{A}}}{{{\rho }_{A}}}$

Factorizamos tanto en el miembro izquierdo, como en el miembro derecho:

$\displaystyle \frac{{{v}_{A}}^{2}-{{v}_{B}}^{2}}{2}=g({{h}_{B}}-{{h}_{A}})-\frac{{{p}_{A}}}{{{\rho }_{A}}}$

Esta será la fórmula que utilizaremos para encontrar la velocidad en A

Datos del problema:

$\displaystyle {{d}_{A}}=70mm\left( \frac{1m}{1000mm} \right)=0.07m$

$\displaystyle {{d}_{B}}=35mm\left( \frac{1m}{1000mm} \right)=0.035m$

$\displaystyle {{h}_{A}}=0m$

$\displaystyle {{h}_{B}}=3.65m$

$\displaystyle {{p}_{A}}=565kPa$

$\displaystyle {{\rho }_{agua}}=1000\frac{kg}{{{m}^{3}}}$

a) Encontrando la velocidad en A

Antes de comenzar a sustituir datos en la fórmula, vamos a calcular las áreas en la sección A, y B

⭕ Calculando el área en A

$\displaystyle {{A}_{A}}=\frac{\pi {{\left( 0.07m \right)}^{2}}}{4}=0.0038{{m}^{2}}$

⭕ Calculando el área en B

$\displaystyle {{A}_{B}}=\frac{\pi {{\left( 0.035m \right)}^{2}}}{4}=0.00096{{m}^{2}}$

Una vez que hemos calculado el área en la secciones, pasemos a sustituir nuestros datos en la fórmula que se redujo de Bernoulli

$\displaystyle \frac{{{v}_{A}}^{2}-{{v}_{B}}^{2}}{2}=g({{h}_{B}}-{{h}_{A}})-\frac{{{p}_{A}}}{{{\rho }_{A}}}$

De esta forma:

$\displaystyle \frac{{{v}_{A}}^{2}-{{v}_{B}}^{2}}{2}=\left( 9.81\frac{m}{{{s}^{2}}} \right)(3.65-0)-\frac{565000Pa}{1000\frac{kg}{{{m}^{3}}}}$

Reduciendo:

$\displaystyle \frac{{{v}_{A}}^{2}-{{v}_{B}}^{2}}{2}=\left( 9.81\frac{m}{{{s}^{2}}} \right)(3.65m)-565$

$\displaystyle \frac{{{v}_{A}}^{2}-{{v}_{B}}^{2}}{2}=35.8065-565$

Pasando a multiplicar a "2" al miembro derecho

$\displaystyle {{v}_{A}}^{2}-{{v}_{B}}^{2}=2\left( 35.8065-565 \right)$

$\displaystyle {{v}_{A}}^{2}-{{v}_{B}}^{2}=2\left( -529.1935 \right)$

Realizando las operaciones en el miembro derecho

$\displaystyle {{v}_{A}}^{2}-{{v}_{B}}^{2}=-1058.387$

Hasta este punto ya no podemos hacer más, tenemos que apoyarnos de otro recurso. Y ese recurso que tenemos a la mano, es la ecuación de continuidad. Qué dice lo siguiente:

$\displaystyle {{A}_{A}}{{v}_{A}}={{A}_{B}}{{v}_{B}}$

Vamos a despejar a la velocidad en B.

$\displaystyle {{v}_{B}}=\frac{{{A}_{A}}{{v}_{A}}}{{{A}_{B}}}$

Ya sabemos cuanto vale el área en A, y cuánto vale el área en B, solamente lo colocamos en los datos:

$\displaystyle {{v}_{B}}=\frac{{{A}_{A}}{{v}_{A}}}{{{A}_{B}}}=\frac{\left( 0.0038{{m}^{2}} \right){{v}_{A}}}{0.00096{{m}^{2}}}$

Simplificando, esto nos da:

$\displaystyle {{v}_{B}}=3.96{{v}_{A}}$

Este valor qué hemos obtenido, lo podemos sustituir en la fórmula que veníamos resolviendo, de esta forma:

$\displaystyle {{v}_{A}}^{2}-{{v}_{B}}^{2}=-1058.387$

Como sabemos que la velocidad en B es 3.96 veces la velocidad en A, entonces sustituimos:

$\displaystyle {{v}_{A}}^{2}-{{\left( 3.96{{v}_{A}} \right)}^{2}}=-1058.387$

Elevando al cuadrado:

$\displaystyle {{v}_{A}}^{2}-15.68{{v}_{A}}^{2}=-1058.387$

Restando:

$\displaystyle -14.68{{v}_{A}}^{2}=-1058.387$

Como ambos miembros son negativos, podemos hacerlos positivos.

$\displaystyle 14.68{{v}_{A}}^{2}=1058.387$

Despejando a la velocidad en A

$\displaystyle {{v}_{A}}^{2}=\frac{1058.387}{14.68}=72.097$

Extrayendo raíz cuadrada:

$\displaystyle {{v}_{A}}=\sqrt{72.097}=8.49\frac{m}{s}$

Como resultado hemos obtenido que la velocidad en el punto A es de 8.49 m/s

Resultado:

$\displaystyle {{v}_{A}}=8.49\frac{m}{s}$

2 Comentarios Publicados

ALBERTO dice:

19 abril, 2024 a las 8:58 am

estos problemas me ayudaron a entender bien el T.D.B. GRACIAS!!!!!!!!!!

Responder
joe dice:

7 julio, 2024 a las 5:41 pm

¿Por qué de 15.68 pasó a 14.68 al restar VA^2?

Responder

Deja una respuesta Cancelar la respuesta