Solución Problema 2 Ley de Senos

En el siguiente ejercicio resuelto se vuelve a plantear el problema del tema: Ley de Senos, se coloca el bosquejo del triángulo y su respectiva solución.

Nivel de Dificultad: ⭐⭐

Solución:

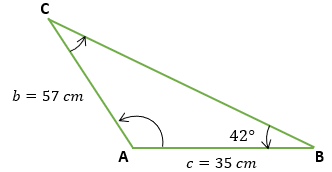
Lo primero que tenemos que hacer, es ir recopilando toda la información que nos proporciona el problema del triángulo, que en este caso sería la distancia "c" , la distancia "b" y el ángulo B

c = 35 cm

b = 57 cm

<B = 42°

En la Ley de Senos es importante tener en cuenta nuestra fórmula para aplicarla según sea el caso, en este ejercicio contamos con el lado "b", así como su ángulo B. Por lo que si tenemos la distancia "c", entonces será mucho más fácil encontrar el ángulo C

Obteniendo el ángulo C

Aplicando la fórmula de ley de senos, tenemos:

$\displaystyle \frac{b}{senB}=\frac{c}{senC}$

Despejando Sen C, obtenemos:

$\displaystyle senC=\frac{c\cdot senB}{b}$

Sustituyendo datos en la fórmula:

$\displaystyle senC=\frac{c\cdot senB}{b}=\frac{(35cm)(sen42{}^\circ )}{57cm}=0.4108$

Despeando C

$\displaystyle \sphericalangle C=arcsen(0.4108)=24.26{}^\circ $

Obteniendo el ángulo A

Aplicando la suma interna de los ángulos de un triángulo, tenemos:

$\displaystyle \sphericalangle A+42{}^\circ +24.26{}^\circ =180{}^\circ $

Despejando a <A

$\displaystyle \sphericalangle A=180{}^\circ -42{}^\circ -24.26{}^\circ $

Simplificando, obtenemos:

$\displaystyle \sphericalangle A=113.74{}^\circ $

Obteniendo el lado a

Para poder encontrar el ultimo elemento de nuestro triángulo, volvemos hacer uso de la ley de senos:

$\displaystyle \frac{a}{senA}=\frac{b}{senB}$

Despejando a la variable "a"

$\displaystyle a=\frac{b\cdot senA}{senB}$

Sustituyendo datos en la fórmula:

$\displaystyle a=\frac{b\cdot senA}{senB}=\frac{(57cm)(sen113.74{}^\circ )}{sen42{}^\circ }=77.97cm$

Resultados:

$\displaystyle \begin{array}{l}a=77.97cm\\\sphericalangle C=24.26{}^\circ \\\sphericalangle A=113.74{}^\circ \end{array}$