Solución Problema 3 de Campo Eléctrico

Con este tercer problema de Campo Electrico, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula de campo eléctrico, pues muchas veces tenemos que pensar también en las cargas "P" que se ilustran para comprender mejor la dirección de la fuerza y el campo eléctrico, es muy importante conocer esta parte, porque ayudará a la comprensión del tema y así poder resolver todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐

Problema 7.- Calcular la magnitud de la intensidad del campo eléctrico en el punto medio P entre dos cargas puntuales cuyos valores son q1 = 9μC y q2 = 4μC , separadas a una distancia de 16cm.

Problema de Campo Eléctrico

Solución:

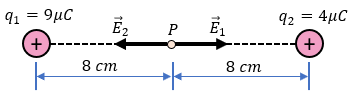
Este problema implica el uso de un punto medio P donde se pretende calcular la magnitud de la intensidad del campo eléctrico, al ser estos vectores de campo eléctrico se realizará una suma vectorial, si no sabe sumar vectores (aquí puede aprender de ello). Bien, entonces comencemos:

Obtener la magnitud de intensidad del campo eléctrico

Datos:

$\displaystyle {{q}_{1}}=9x{{10}^{-6}}C$

$\displaystyle {{q}_{2}}=4x{{10}^{-6}}C$

$\displaystyle d=8cm\left( \frac{1m}{100cm} \right)=0.08m$

Aunque la distancia total sea de 16 centímetros, se debe tomar a 8 centímetros puesto que es a la mitad donde está localizado el punto P

a) Obtener la magnitud de intensidad del campo eléctrico

Si observamos la imagen, vemos que los campos eléctricos van dirigidos hacía las mismas cargas, esto es porque las cargas son totalmente positivas. Ahora, al saber esto también debemos analizar que en las sumas vectoriales lo que va hacía la derecha es positivo, y lo que va hacía la izquierda es negativo, esto pasa si nuestro marco de referencia es similar a lo que marca un plano cartesiano. Puede que en otros casos sea distinto, pero por lo general en los libros de Física lo manejan de esta manera:

El campo eléctrico de la primera carga va hacía la derecha (será positivo) , el campo eléctrico de nuestra segunda carga va hacía la izquierda (será negativo). Entonces decimos que:

$\displaystyle {{E}_{R}}={{E}_{1}}+\left( -{{E}_{2}} \right)$

Por fórmula esto es:

$\displaystyle {{E}_{R}}=\frac{K{{q}_{1}}}{{{d}^{2}}}+\left( -\frac{K{{q}_{2}}}{{{d}^{2}}} \right)$

Como la constante "K" y la distancia son las mismas "d" , entonces podemos factorizarlo.

$\displaystyle {{E}_{R}}=\frac{K{{q}_{1}}}{{{d}^{2}}}+\left( -\frac{K{{q}_{2}}}{{{d}^{2}}} \right)=\frac{K}{{{d}^{2}}}\left( {{q}_{1}}-{{q}_{2}} \right)$

Es decir:

$\displaystyle {{E}_{R}}=\frac{K}{{{d}^{2}}}\left( {{q}_{1}}-{{q}_{2}} \right)$

Ahora si podemos sustituir nuestros datos en la fórmula:

$\displaystyle {{E}_{R}}=\frac{K}{{{d}^{2}}}\left( {{q}_{1}}-{{q}_{2}} \right)=\frac{9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}}{{{(0.08m)}^{2}}}\left( 9x{{10}^{-6}}C-4x{{10}^{-6}}C \right)=7.03x{{10}^{-6}}\frac{N}{C}$

Es decir que nuestra intensidad de campo eléctrico es de 7.03x10^(6) N/C

Resultado:

$\displaystyle {{E}_{R}}=7.03x{{10}^{-6}}\frac{N}{C}$

5 Comentarios Publicados

Mora dice:

22 febrero, 2023 a las 10:27 am

Muchas gracias, me resultó muy útil

Responder
ert4 dice:

4 mayo, 2023 a las 10:12 am

Q en ahi no es 10^3 en vez de 10^(-6)

Responder
Esme dice:

1 junio, 2023 a las 10:12 pm

Genial, me re ayudaron.Muchas gracias:3

Responder
Luis Bustamante dice:

26 junio, 2023 a las 2:39 pm

Muchas gracias!! 😊 (solo hay una errata en la respuesta dos veces escrita en el problema 7: el signo del exponente debe ser positivo: 7.03 X 10^6 N/C) Felicidades!!

Responder
[email protected] dice:

2 abril, 2024 a las 12:41 pm

Muchas gracias me sirvió de muchísimo

Responder

Deja una respuesta Cancelar la respuesta