Suma de Vectores - Método Analítico

En Física es común encontrarse una suma de cantidades vectoriales, y aunque podemos recurrir a diversos métodos como el del triángulo, del polígono o el paralelogramo, es importante tener en cuenta que la forma analítica nos conducirá a un resultado más exacto. Ahora veamos que necesitamos para comprender por completo el método analítico, además de resolver varios ejercicios paso a paso.

En el método analítico es posible aplicar el teorema de pitágoras solamente si los dos vectores forman un ángulo de 90°, de otra forma tendremos que aplicar la Ley de Cosenos, y si se desea calcular el ángulo de la resultante es posible también recurrir a la Ley de Senos.

✅ Suma de dos vectores angulares o concurrentes

En varios libros, muchos autores también relacionan el método analítico como una suma de vectores angulares o concurrentes, recordemos que los vectores los podemos agrupar por el tipo, en caso de tener dudas, favor de revisar > Tipos de Vectores

Veamos la manera general de sumar dos vectores, y de entender como se nos puede presentar diversos problemas:

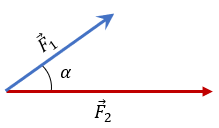
Para realizar la suma analítica, basta con trazar la resultante a partir de sus proyecciones como vectores deslizantes, de tal manera que:

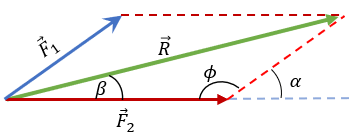
Realizar estos movimientos nos favorece mucho la forma de solución de la resultante, es por ello que si deseamos sumar dos vectores, será mucho más fácil.

📄 Pasos para el Método Analítico en la suma de Vectores

El método analítico, a diferencia de los métodos que podemos ver en este sitio web, no requiere la utilización de la forma gráfica de los vectores. Se puede llevar a cabo sin realizar un solo dibujo.En el ejemplo que se analiza en los ejercicios resueltos, se podra observar porque no es necesario, sin embargo aquí en el sitio web, lo utilizaremos. Para llevar a cabo el procedimiento del método analítico, debemos de considerar los siguientes puntos.

1. Obtener las componentes rectangulares de todos los vectores que se van a sumar.
2. Sumar todas las componentes en x de todos los vectores para obtener la componente en x del vector resultante.
3. Sumar todas las componentes en y de todos los vectores para obtener la componente en y del vector resultante.
4. Obtener la magnitud y el ángulo del vector resultante a partir de sus componentes rectangulares.

Para poder apreciar de mejor forma, este método, veamos algunos ejemplos resueltos.

📙 Ejercicios Resueltos de Suma de Vectores (Método Analítico)

Veamos el siguiente ejercicio.

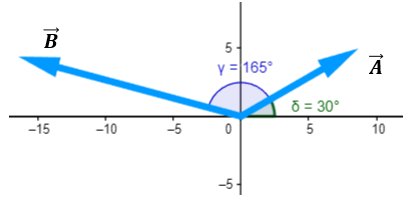
Solución:

Primero es necesario obtener las componentes rectangulares de cada vector. Para el vector A la componente en el eje x es:

$\displaystyle {{A}_{x}}=A\cos \alpha =10N\cdot \cos \left( {30{}^\circ } \right)=10N\cdot 0.866=8.66N$

La componente en el eje y es:

$\displaystyle {{A}_{y}}=Asen\alpha =10N\cdot sen\left( {30{}^\circ } \right)=10N\cdot 0.5=5N$

Para el vector B, la componente en el eje x es,

$\displaystyle {{B}_{x}}=B\cos \alpha =17N\cdot \cos \left( {165{}^\circ } \right)=17N\cdot \left( {-0.966} \right)=-16.42N$

La componente en el eje y es:

$\displaystyle {{B}_{y}}=Bsen\alpha =17N\cdot sen\left( {165{}^\circ } \right)=17N\cdot \left( {0.259} \right)=4.40N$

Al obtener todas las componentes, se obtienen las componentes rectangulares del vector resultante. De tal modo que al sumar las componentes rectangulares en el eje x se obtiene:

$\displaystyle {{R}_{x}}={{A}_{x}}+{{B}_{x}}=8.66N+\left( {-16.42N} \right)=8.66N-16.42N=-7.76N$

$\displaystyle {{R}_{y}}={{A}_{y}}+{{B}_{y}}=5N+4.40N=9.40N$

Las componentes del vector resultante son:

$\displaystyle \vec{R}=\left( {-7.76,9.40} \right)N$

Para encontrar la magnitud del vector resultante, se utiliza el teorema de Pitágoras:

$\displaystyle \vec{R}=\sqrt{{{{R}_{x}}^{2}+{{R}_{y}}^{2}}}=\sqrt{{{{{\left( {-7.76N} \right)}}^{2}}+{{{\left( {9.40N} \right)}}^{2}}}}$

$\displaystyle \vec{R}=\sqrt{{{{R}_{x}}^{2}+{{R}_{y}}^{2}}}=\sqrt{{60.22{{N}^{2}}+88.36{{N}^{2}}}}=\sqrt{{148.58{{N}^{2}}}}$

$\displaystyle \vec{R}=12.19N$

El ánulo del vector resultante, se obtiene mediante la tangente del ángulo:

$\displaystyle \tan \alpha =\frac{{{{A}_{y}}}}{{{{A}_{x}}}}=\frac{{9.40N}}{{-7.76N}}=-1.21$

El ángulo β es entonces:

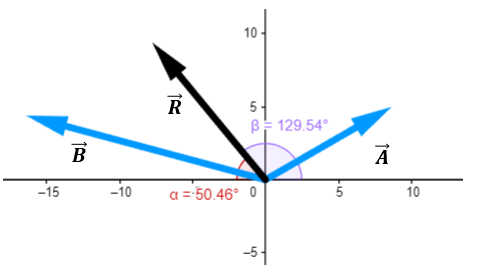
$\displaystyle \alpha ={{\tan }^{{-1}}}(-1.21)=-50.46{}^\circ $

Pero el ángulo debe ser un valor mayor a 0° y menor a 360°. Observa los vectores en su forma gráfica de este ejemplo, el ángulo obtenido con la calculadora corresponde al que se forma respecto a la parte negativa del eje x y en sentido de las manecillas del reloj. Ese no es el ángulo que se necesita, sino el ángulo suplementario. Así, el ángulo buscado es:

$\displaystyle \beta =180{}^\circ -50.46{}^\circ =129.54{}^\circ $

Solución:

Vamos a realizar un diagrama de cuerpo libre, para entender mucho mejor el gráfico, en dado caso haya confusión con un diagrama será más claro.

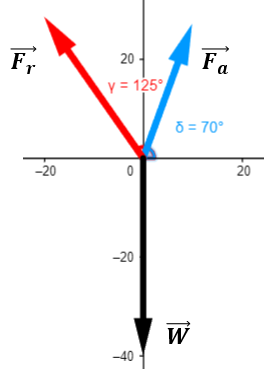
Vamos a determinar las componentes de la fuerza que ejerce la persona de rojo: $\displaystyle \overrightarrow{{{{F}_{R}}}}$

$\displaystyle {{F}_{x}}_{{_{r}}}=F\cos \gamma =\left( {35N} \right)\cos \left( {125{}^\circ } \right)=-20.075N$

$\displaystyle {{F}_{y}}_{{_{r}}}=Fsen\gamma =\left( {35N} \right)sen\left( {125{}^\circ } \right)=28.67N$

Ahora vamos a determinar las componentes de la fuerza que ejerce la persona de azul: $\displaystyle \overrightarrow{{{{F}_{A}}}}$

$\displaystyle {{F}_{x}}_{{_{a}}}=F\cos \delta =\left( {29N} \right)\cos \left( {70{}^\circ } \right)=9.918N$

$\displaystyle {{F}_{y}}_{{_{a}}}=Fsen\delta =\left( {29N} \right)sen\left( {70{}^\circ } \right)=27.251N$

Ahora procedemos a calcular el peso de la bolsa, es decir la fuerza de la tierra para jalar la bolsa hacía abajo.

$\displaystyle {{F}_{x}}_{{_{w}}}=F\cos \beta =\left( {45N} \right)\cos \left( {270{}^\circ } \right)=0N$

$\displaystyle {{F}_{y}}_{{_{w}}}=Fsen\beta =\left( {45N} \right)sen\left( {270{}^\circ } \right)=-45N$

Sumando las componentes rectangulares del eje x se obtiene:

$\displaystyle {{F}_{R}}_{{_{x}}}={{F}_{{{{x}_{r}}}}}+{{F}_{{{{x}_{a}}}}}+{{F}_{{{{x}_{w}}}}}=-20.075N+9.918N+0N$

$\displaystyle {{F}_{R}}_{{_{x}}}=-10.157N$

Sumando las componentes rectangulares del eje y se obtiene:

$\displaystyle {{F}_{R}}_{{_{y}}}={{F}_{{{{y}_{r}}}}}+{{F}_{{{{y}_{a}}}}}+{{F}_{{{{y}_{w}}}}}=28.67N+27.251N-45N$

$\displaystyle {{F}_{R}}_{{_{x}}}=10.921N$

El vector resultante posee las coordenadas:

$\displaystyle \overrightarrow{{{{F}_{R}}}}=\left( {-10.157,10.921} \right)N$

Utilizando el teorema de pitágoras para determinar la magnitud del vector:

$\displaystyle {{F}_{R}}=\sqrt{{{{{\left( {-10.157N} \right)}}^{2}}+{{{\left( {10.921N} \right)}}^{2}}}}$

$\displaystyle {{F}_{R}}=14.914N$

Al determinar el ángulo:

$\displaystyle \phi ={{\tan }^{{-1}}}\left( {\frac{{{{F}_{{{{R}_{y}}}}}}}{{{{F}_{{{{R}_{x}}}}}}}} \right)={{\tan }^{{-1}}}\left( {\frac{{10.921N}}{{-10.157N}}} \right)=-47.08{}^\circ $

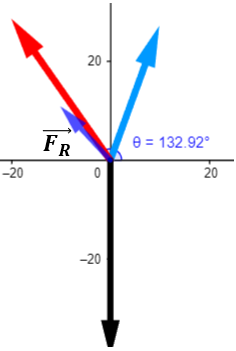
Al observar que el ángulo obtenido corresponde al que se forma con respecto a la parte negativa del eje x y en el sentido de las manecillas del reloj. Ese no es el ángulo que se necesita, sino el ángulo suplementario. Así, al ángulo buscado es:

$\displaystyle \theta =180{}^\circ -47.08{}^\circ =132.92{}^\circ $

De forma gráfica, la suma de los tres vectores se vería así:

Solución: 

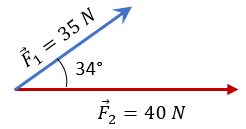
Aunque este problema se resolvió con el método del triángulo, en este problema, veremos como resolverlo mediante el método analítico.

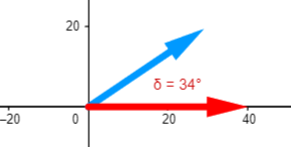
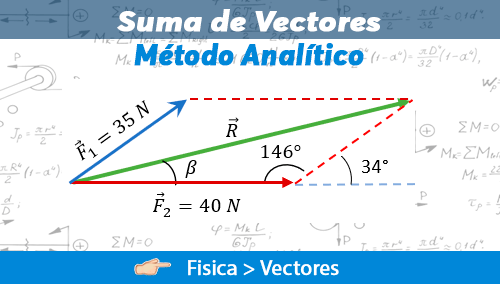
Observe que la $\displaystyle {{F}_{1}}$ posee un ángulo de 34° y la $\displaystyle {{F}_{2}}$ posee un ángulo de 0°.

Vamos a obtener las componentes rectangulares de la fuerza 1

$\displaystyle {{F}_{1}}_{x}=(35N)\cos (34{}^\circ )=29.016N$

$\displaystyle {{F}_{1}}_{y}=(35N)sen(34{}^\circ )=19.572N$

Ahora vamos a obtener las componentes rectangulares de la fuerza 2

$\displaystyle {{F}_{2}}_{x}=(40N)\cos (0{}^\circ )=40N$

$\displaystyle {{F}_{2}}_{y}=(40N)sen(0{}^\circ )=0N$

Sumando las componentes rectangulares del eje x se obtiene:

$\displaystyle {{F}_{R}}_{x}={{F}_{{1x}}}+{{F}_{{2x}}}=29.016N+40N=69.016N$

Sumando las componentes rectangulares del eje y se obtiene:

$ \displaystyle {{F}_{R}}_{y}={{F}_{{1y}}}+{{F}_{{2y}}}=19.572N+0N=19.572N$

El vector resultante, posee las coordenadas:

$\displaystyle \overrightarrow{{{{F}_{R}}}}=\left( {69.016,19.572} \right)N$

Utilizando el teorema de pitágoras para determinar la magnitud del vector, obtenemos:

$\displaystyle \overrightarrow{{{{F}_{R}}}}=\sqrt{{{{{\left( {69.016N} \right)}}^{2}}+{{{\left( {19.572N} \right)}}^{2}}}}$

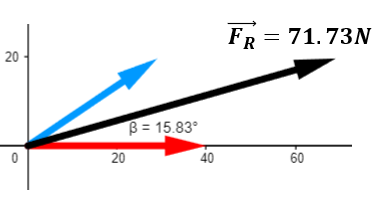
$\displaystyle \overrightarrow{{{{F}_{R}}}}=71.73N$

Al determinar el ángulo:

$\displaystyle \phi ={{\tan }^{{-1}}}\left( {\frac{{{{F}_{{{{R}_{y}}}}}}}{{{{F}_{{{{R}_{x}}}}}}}} \right)={{\tan }^{{-1}}}\left( {\frac{{19.572N}}{{69.016N}}} \right)={{15.83}^{{}^\circ }}$

De forma, gráfica la resultante se vería de la siguiente forma:

Solución: 

Vamos a realizar un bosquejo del trayecto del avión, los 300 km al norte, y después el movimiento por la derecha a una distancia desconocida, y finalmente la dirección hacia su punto inicial el cual fue de 500 km, si nosotros trasladamos esto en un problema de los vectores, vamos analizarlo mediante sus componentes rectangulares, es decir.

Vamos asignar las componentes de la siguiente forma:

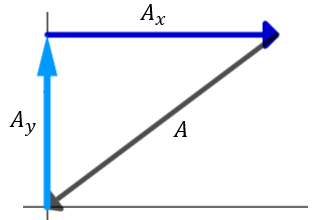
El valor que se pide determinar es la componente $\displaystyle {{A}_{x}}$ , por lo tanto, de la fórmula tenemos:

$\displaystyle A=\sqrt{{{{A}_{x}}^{2}+{{A}_{y}}^{2}}}$

Despejamos $\displaystyle {{{A}_{x}}}$

$\displaystyle {{A}_{x}}=\sqrt{{{{A}^{2}}-{{A}_{y}}^{2}}}$

$\displaystyle {{A}_{x}}=\sqrt{{{{A}^{2}}-{{A}_{y}}^{2}}}=\sqrt{{{{{\left( {500km} \right)}}^{2}}-{{{\left( {300km} \right)}}^{2}}}}$

$\displaystyle {{A}_{x}}=\sqrt{{1600000k{{m}^{2}}}}$

$\displaystyle {{A}_{x}}=400km$

Por lo tanto, podemos concluir que el avión recorrió 400 km hacia el este.

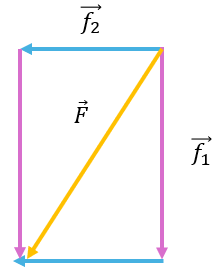
Solución:

Observemos que al no tener una inclinación las fuerzas, tanto la del balón como la de la resistencia del aire, entonces no habra un valor de su componente, de forma gráfica tenemos el siguiente diagrama de cuerpo libre, considerando los ángulos que se forman desde el eje horizontal.

a) El módulo F de la fuerza resultante sobre la pelota

Las componentes ortogonales de las fuerzas serán las siguientes:

Peso:

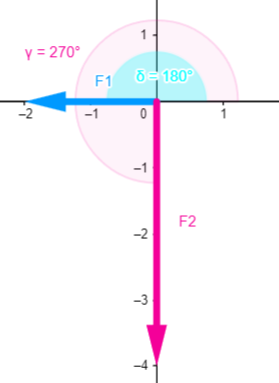
$\displaystyle {{f}_{{1x}}}={{f}_{1}}\cos \gamma =2N\cos \left( {180{}^\circ } \right)=-2N$

$\displaystyle {{f}_{{1y}}}={{f}_{1}}sen\gamma =2Nsen\left( {180{}^\circ } \right)=0N$

Fuerza del viento:

$\displaystyle {{f}_{{2x}}}={{f}_{2}}\cos \delta =4N\cos \left( {270{}^\circ } \right)=0N$

$\displaystyle {{f}_{{2y}}}={{f}_{2}}sen\delta =4Nsen\left( {270{}^\circ } \right)=-4N$

El vector resultante es:

$\displaystyle {{F}_{x}}={{f}_{{1x}}}+{{f}_{{2x}}}=-2N+0N=-2N$

$\displaystyle {{F}_{y}}={{f}_{{1y}}}+{{f}_{{2y}}}=0N+\left( {-4N} \right)=-4N$

Obteniendo la magnitud del vector:

$\displaystyle F=\sqrt{{{{{\left( {-2N} \right)}}^{2}}+{{{\left( {-4N} \right)}}^{2}}}}=4.47N$

b) Obteniendo la dirección y sentido de la fuerza resultante.

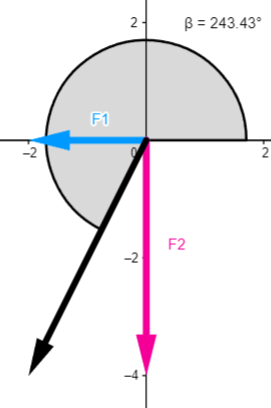
$\displaystyle \alpha ={{\tan }^{{-1}}}\left( {\frac{{{{F}_{y}}}}{{{{F}_{x}}}}} \right)={{\tan }^{{-1}}}\left( {\frac{{-4N}}{{-2N}}} \right)={{\tan }^{{-1}}}(2)=63.43{}^\circ $

Sin embargo el ángulo de 64.43° es solo el ángulo comprendido en el tercer cuadrante, por lo que le sumaremos los 180° desde el lado positivo respecto a las manecillas del reloj:

$\displaystyle \beta =180{}^\circ +63.43{}^\circ =243.43{}^\circ $

Qué sería lo que se estaba buscando.