Producto Escalar - Ejercicios Resueltos
El producto escalar, o también conocido como producto punto o producto interno, es una operación matemática para multiplicar el módulo de dos vectores por el ángulo que forman entre ellos y dar como resultado un valor escalar, o bien una cantidad real. En la siguiente imagen vemos a los dos vectores y el ángulo que forman ambos.
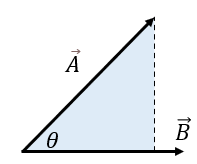
Dados los vectores A y B, su producto escalar o interno se representa por A⋅B y se define como el producto de sus módulos por el coseno del ángulo θ que forman, esto es:
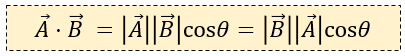
Debemos darnos cuenta que el resultado de este producto A⋅B nos proporcionará un número real (positivo, negativo o nulo) y no un vector.
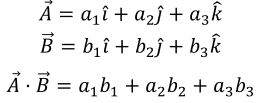
👉 Propiedades del Producto Escalar
Como toda operación entre vectores, hay reglas que cumplir y las reglas las hemos colocado en la siguiente tabla para poder resolver ejemplos y ejercicios sin complicación alguna.
Una vez considerando la tabla de propiedades del producto escalar, punto o interno. Podemos pasar a resolver algunos ejercicios.
📄 Ejercicios Resueltos de Producto Escalar
Problema 1. Dado los vectores a y b que forman entre si un ángulo de 120°, y sabiendo que |a| = 3 y |b| = 5, calcular: a⋅b
Solución:
En este problema tenemos el módulo tanto del vector "a" como del vector "b", así como también el ángulo, entonces procedemos aplicar la fórmula:
$\displaystyle \overrightarrow{a}\cdot \overrightarrow{b}=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|\cos \theta $
Sustituyendo nuestros datos en la fórmula:
$\displaystyle \overrightarrow{a}\cdot \overrightarrow{b}=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|\cos \theta =(3)(5)\cos 120{}^\circ =-7.5$
Por lo que obtenemos un valor escalar de -7.5
Problema 2. Calcule el producto punto de los vectores a⋅b
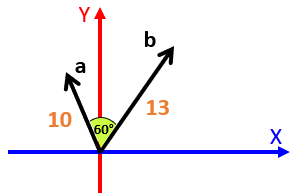
Solución:
Si observamos bien, tenemos el módulo del vector a = 10 y el módulo del vector b = 13, y entre ambos se forma un ángulo de 60° por lo tanto podemos nuevamente recurrir a nuestra fórmula:
$\displaystyle \overrightarrow{a}\cdot \overrightarrow{b}=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|\cos \theta $
y sustituir nuestros datos:
$\displaystyle \overrightarrow{a}\cdot \overrightarrow{b}=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|\cos \theta =(10)(13)\cos 60{}^\circ =65$
Obtenemos un valor escalar de 65
Problema 3. Calcule el producto escalar de los vectores a⋅b dada la siguiente imagen
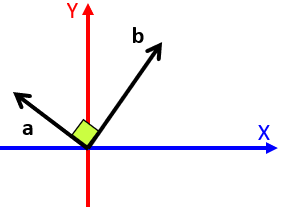
Solución:
A pesar de que este problema no nos da los módulos de los vectores "a" y "b" vamos a tomar en cuenta el ángulo entre ambos, de 90° debido a que es un ángulo recto, entonces aplicamos nuestra fórmula:
$\displaystyle \overrightarrow{a}\cdot \overrightarrow{b}=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|\cos \theta $
Sustituyendo datos:
$\displaystyle \overrightarrow{a}\cdot \overrightarrow{b}=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|\cos \theta =(a)(b)\cos 90{}^\circ =0$
Por lo que obtenemos un valor de 0
Es decir que:
Cuando dos vectores forman ángulos rectos entre sí, su producto escalar es cero
Este ejemplo nos ayudará mucho para encontrar el valor de dos vectores que tienen 90 grados entre ambos.
Problema 4. El Vector a tiene magnitud 3√2, vector b tiene magnitud 5 y el ángulo entre a y b es de 135 °
Solución:
Para darle solución a este ejemplo, veamos nuestra fórmula a utilizar:
$\displaystyle \overrightarrow{a}\cdot \overrightarrow{b}=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|\cos \theta $
Sustituyendo nuestros datos:
$\displaystyle \overrightarrow{a}\cdot \overrightarrow{b}=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|\cos \theta =(3\sqrt{2})(5)\cos 135{}^\circ =15\sqrt{2}\cos 135{}^\circ $
Resolviendo, obtenemos:
$\displaystyle \overrightarrow{a}\cdot \overrightarrow{b}=15\sqrt{2}\cos 135{}^\circ =-15$
Por lo que el resultado es -15
Temas que podrían interesarte 👇