Propiedades de los Vectores

Amig@s hoy hablaremos de uno de los temas centrales de la Física, y al terminar de leer este artículo y los demás de la sección de vectores, aprenderás a resolver cualquier problema que tenga que ver con cantidades vectoriales, sea suma, resta, multiplicación, etc..

Dos tipos de Magnitudes (Escalares y Vectoriales)

Existen dos tipos de magnitudes en Física, las magnitudes escalares y las magnitudes vectoriales, aunque existen también otros tipos de magnitudes como las tensoriales, pero dicha magnitud se restringe a darle explicación en este blog, sin embargo lo puedes aprender en álgebra lineal del blog de Laplacianos.

Magnitud Escalar

La magnitud escalar es aquella magnitud que no posee dirección, ni sentido, es decir, aquellas magnitudes que solamente se expresa en una cantidad y unidad de medida, por ejemplo: la masa, el volumen, la temperatura, entre otros.

Magnitud Vectorial

Por otro lado tenemos las magnitudes vectoriales, que a diferencia de las escalares, éstas si poseen dirección y sentido, además de un punto de aplicación. Podemos citar algunos ejemplos como la velocidad, la aceleración, la fuerza, el desplazamiento, etc.. Es muy diferente a lo que una cantidad escalar representa.

Características de un Vector

Esto de aquí abajo es un vector, algunos les llaman "vector libre", ya que dicho vector no está actuando en algún punto de aplicación 😀

Para que un vector exista, debe poseer ciertas características. Aquí vemos que características debe de tener.

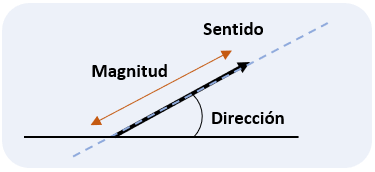
Magnitud

La magnitud en un vector indica el valor numérico del vector a través de una unidad de medida.

Dirección

Por lo general los vectores poseen una dirección, y pueden representarse mediante un plano cartesiano rectangular, entre cuatro cuadrantes y con la división de 90° cada uno, el lado positivo comienza a partir del eje "x".

Sentido

Para representar el sentido en un vector, se le asigna una punta de flecha e indica hacía donde se dirige dicho vector, donde libremente puede ser hacía arriba, abajo, derecha, e izquierda.

Tipos de Vectores

A pesar de que un vector es un vector (en definición), existen algunos tipos de vectores que iremos viendo a través de este blog, pero que es necesario mencionarlos para entender mucho mejor el tema.

Vectores Coplanares

Los vectores coplanares, son aquellos vectores que están sobre el mismo plano, en dos ejes. Por ejemplo:

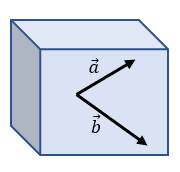
Vectores No Coplanares

Como su nombre lo dice, los vectores no coplanares son aquellos vectores que no están en el mismo plano, tal como se ilustra en la imagen:

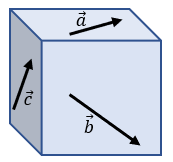
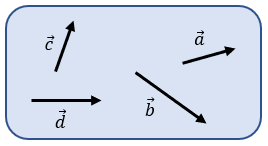
Vectores Libres

Son aquellos vectores que no posee un punto de aplicación en particular, tal como se ilustra en la imagen:

Vectores Colineales

Son aquellos vectores que se encuentran en la misma dirección o línea de acción, tal como se ilustra en la imagen:

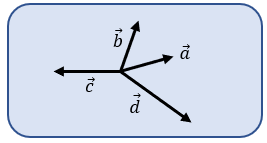
Vectores Concurrentes o angulares

Los vectores concurrentes son aquellos vectores que se cruzan en algún punto sobre la misma dirección o línea de acción, y asumen también el nombre de vectores angulares que son aquellos que forman un ángulo entre ellos. tal como se ilustra en la imagen:

Propiedades de los vectores

Los vectores poseen propiedades muy importantes, y en este artículo hablaremos de ellas:

a) Igualdad de dos vectores

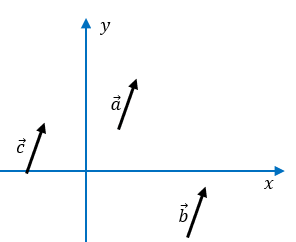
Los tres vectores son iguales, tienen la misma magnitud, dirección y sentido, en lo único que no son iguales es en su punto de aplicación.

b) Suma de los Vectores

Así también las magnitudes escalares no se pueden sumar si no tienen las mismas unidades. En el siguiente artículo, veremos como sumar los vectores de manera algebraica y gráfica. Por ahora basta

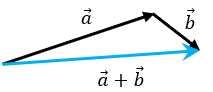
c) Negativo de un vector (Resta de vectores)

Tomando el ejemplo anterior de la suma de vectores, intentaremos restarlos:

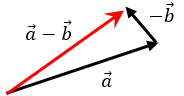
Nota: Hemos cambiado la dirección del vector b

d) Ley conmutativa de la adición de vectores

e) Propiedad de Vectores libres

Esta propiedad es importante, ya que nos permitirá realizar ejercicios de manera gráfica usando métodos como (el paralelogramo, el polígono, el triángulo).