Método del Triángulo + Ejercicios Resueltos (Vectores)

Para poder aprender a sumar vectores primero debemos aprender muy bien las propiedades y características de cada vector, una vez entendiendo sus propiedades podemos seguir el algoritmo para poder realizar el cálculo de manera efectiva y correcta y así resolver cualquier problema que se nos presente 😎

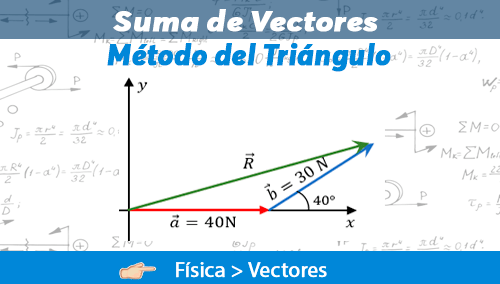
🔼 ¿Qué es el Método del Triángulo?

El método del triángulo es un método que consiste en trasladar los vectores sin cambiar sus propiedades de tal forma que la punta de la flecha de uno se conecta con el origen del otro. De esta forma el vector resultante se representa por la flecha que une la punta libre con el origen libre, y de ahí es que se formará un triángulo que se puede representar mediante la letra R, esto puede ser de ésta manera, sino también puede usarse alguna u otra variable para representar a la resultante.

👉 Pasos para realizar el método del triángulo

Vamos a realizar paso a paso lo que se necesita para realizar una suma de vectores por éste método de manera correcta.

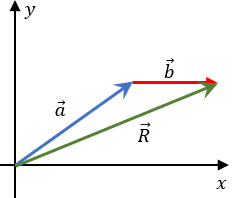
Paso 1: Vamos a imaginar dos vectores, de la siguiente manera:

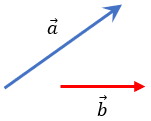
Paso 2: Vamos a posicionar al vector a en el origen de un plano cartesiano.

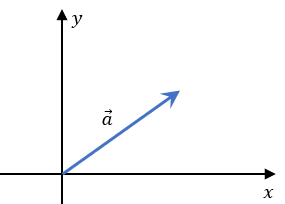
Paso 3: Vamos a colocar al vector b en la punta de la flecha del vector a.

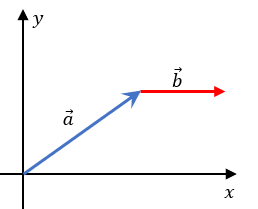
Paso 4: Ahora vamos a unir el origen con la punta de la flecha del vector b, esto es para formar el vector resultante (la suma de ambos vectores).

✅ Ejercicios Resueltos del método del triángulo

Para entender mejor el tema, veamos algunos ejemplos resueltos para el método del triángulo.

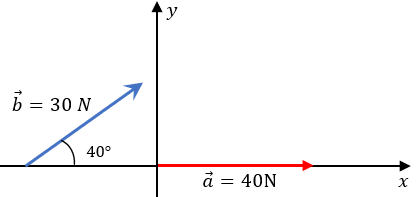
Solución: Siguiendo los pasos colocados anteriormente, podemos unir la punta de la flecha del vector a, en el la cola del vector b, y trazar la resultante, de tal forma que nuestro triángulo quede de la siguiente forma:

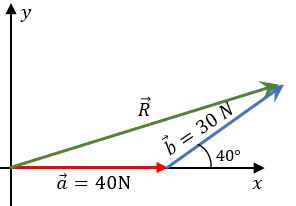
Si hacemos bien el análisis matemático del ángulo, sabremos que un ángulo complementario está dentro del triángulo. Si 180° le quitamos 40° vamos a obtener el valor de dicho ángulo es decir:

$\displaystyle 180{}^\circ -40{}^\circ =140{}^\circ $

Ahora pasamos a tener un triángulo oblicuángulo que podemos resolver mediante la ley de cosenos.

$\displaystyle {{R}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos (140{}^\circ )$

Despejando a R

$\displaystyle R=\sqrt{{{a}^{2}}+{{b}^{2}}-2ab\cos (140{}^\circ )}$

Sustituyendo nuestros datos:

$\displaystyle R=\sqrt{{{\left( 40N \right)}^{2}}+{{\left( 30N \right)}^{2}}-2\left( 40N \right)\left( 30N \right)\cos (140{}^\circ )}$

$\displaystyle R=\sqrt{2500{{N}^{2}}-2400{{N}^{2}}\cos (140{}^\circ )}$

$\displaystyle R=\sqrt{{2500{{N}^{2}}-(-1838.51{{N}^{2}})}}$

Nos damos cuenta que el coseno de 140 dio negativo, con el negativo de la fórmula de la ley de cosenos, tendremos que aplicar (el menos por menos)

$\displaystyle R=\sqrt{{2500{{N}^{2}}+1838.51{{N}^{2}}}}$

Sumando

$\displaystyle R=\sqrt{{4338.51{{N}^{2}}}}$

Aplicando la raíz cuadrada, esto nos da:

$\displaystyle R=65.87N$

Qué vendría a ser la suma de los dos vectores 😀

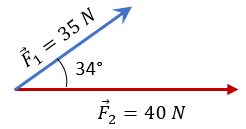
Solución: Si dichos vectores se deslizan podemos trazar la resultante, de tal forma que:

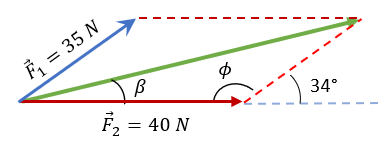
A simple vista podemos calcular el ángulo Φ, puesto que es un ángulo complementario con los 34° que forman parte del vector F1 con la horizontal, entonces podemos decir que:

$\displaystyle \phi =180{}^\circ -34{}^\circ =146{}^\circ $

Para poder encontrar la resultante, tendremos que recurrir a la ley de cosenos.

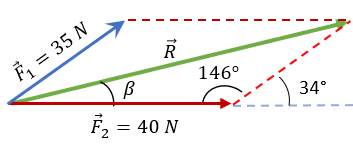
$\displaystyle R=\sqrt{{{35}^{2}}+{{40}^{2}}-2(35)(40)cos(146{}^\circ )}$

$\displaystyle R=\sqrt{1225+1600-(-2321.30)}$

$\displaystyle R=\sqrt{5146.30}$

Obteniendo la raíz cuadrada:

$\displaystyle R=71.73N$

Obteniendo el ángulo de la resultante:

Para obtener el ángulo de la resultante, que le hemos colocado ángulo beta "β".

Aplicamos la ley de senos, de tal manera que la relación del ángulo desconocido nos quede de la siguiente manera:

$\displaystyle \frac{{{F}_{1}}}{sen\beta }=\frac{R}{sen146{}^\circ }$

Despejando a "Sen β"

$\displaystyle sen\beta =\frac{{{F}_{1}}sen146{}^\circ }{R}=\frac{\left( 35N \right)sen146{}^\circ }{71.73N}=\frac{19.57N}{71.73N}=0.2728$

Despejando a "Beta"

$\displaystyle \beta =se{{n}^{-1}}\left( 0.2728 \right)=15.83{}^\circ $

Por lo que la resultante tiene una magnitud de 71.73 N y un ángulo de 15.83°

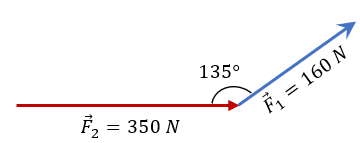
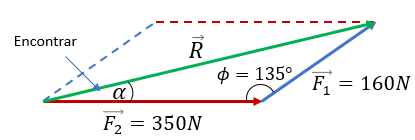
Solución: Si hemos entendido el ejercicio anterior, será mucho más sencillo comprender este ejemplo. Hagamos las proyecciones correspondientes y tracemos la resultante:

Sabiendo que el ángulo ( Φ ) es de 135°, entonces aplicamos la fórmula de la ley de cosenos.

$\displaystyle R=\sqrt{{{160}^{2}}+{{350}^{2}}-2(160)(350)cos({{135}^{{}^\circ }})}$

Luego

$\displaystyle R=\sqrt{{25600+122500-\left( {-79195.96} \right)}}$

$\displaystyle R=\sqrt{{227295.96}}$

Obteniendo la raíz cuadrada:

$\displaystyle R=476.76N$

Obteniendo el ángulo de la resultante:

Nuevamente aplicaremos lo mismo que el ejemplo 1, con los datos que tenemos podemos decir mediante la ley de senos:

$\displaystyle \frac{R}{{sen135{}^\circ }}=\frac{{{{F}_{1}}}}{{sen\alpha }}$

Despejando a sen α

$\displaystyle sen\alpha =\frac{{{{F}_{1}}sen135{}^\circ }}{R}$

Sustituyendo los valores en la fórmula:

$\displaystyle sen\alpha =\frac{{{{F}_{1}}sen135{}^\circ }}{R}=\frac{{\left( {160} \right)sen135{}^\circ }}{{476.76}}=0.237$

Obteniendo el ángulo:

$\displaystyle \alpha =se{{n}^{{-1}}}\left( {0.237} \right)=13.71{}^\circ $

Por lo que en este problema la resultante tiene una magnitud de 476.76 N y un ángulo de 13.71°

Con esto damos por finalizado el ejercicio. 😎