Solución Problema 3 de Ecuación de Continuidad

Con este tercer problema de Ecuación de Continuidad el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula del Gasto y Flujo y hacer uso de incorporarla para futuros cálculos que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐⭐

Problema 5.- Un jardinero usa una manguera para llenar una cubeta de 30 litros, el jardinero observa que tarda 2 minutos en llenar la cubeta. A la manguera se le conecta una boquilla con abertura de 0.5 cm² de área de sección transversal ¿a qué velocidad saldrá el chorro de agua?

Ecuación de Continuidad Ejemplos

Solución:

La solución de este problema es más complejo que los anteriores. Pero no lo es en cuestión de cálculo. Sino en razonamiento, puesto que si analizamos los datos del problema notaremos que nos harán falta algunos datos para solamente utilizar la fórmula, entonces es ahí donde debemos ingeniar la forma de solución del problema. Recordar que el Gasto juega un papel muy importante en el tema de continuidad, si no consideramos esto, entonces posiblemente no podamos resolver correctamente el problema.

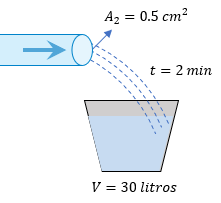
Obtener la velocidad a la que saldrá el chorro de agua

Datos:

$\displaystyle G=\frac{30l}{2\min }=15\frac{l}{\min }$

$\displaystyle {{A}_{2}}=0.5c{{m}^{2}}$

a) Obtener la velocidad a la que saldrá el chorro de agua

Recordemos que la fórmula de continuidad o ecuación de continuidad es de la siguiente forma:

$\displaystyle {{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}$

Sin embargo el problema nos pide encontrar la velocidad del chorro, es decir; la velocidad final "V2", entonces despejamos:

$\displaystyle {{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}$

Pero si analizamos los datos, no tenemos ni siquiera una velocidad inicial ni un área inicial. ¿Cómo podríamos encontrar entonces esos datos?. Aquí es donde tenemos que pensar, y recordar que la definición de gasto, es de entender que una manguera por donde sale el chorro de agua le toma 2 minutos llenar una cubeta de 30 litros, o sea el gasto es el volumen de un líquido que fluye por un determinado tiempo.

El gasto lo podemos escribir de estas dos formas:

$\displaystyle G=\frac{V}{t}$

o también como:

$\displaystyle G=Av$

Es lógico que como se trata de un chorro inicial que llenó la cubeta de agua, lo podamos escribir de esta forma también:

$\displaystyle G={{A}_{1}}{{v}_{1}}$

Nuestra fórmula para encontrar "V2" la podemos reescribir de esta forma:

$\displaystyle {{v}_{2}}=\frac{G}{{{A}_{2}}}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{v}_{2}}=\frac{G}{{{A}_{2}}}=\frac{15\frac{l}{\min }}{0.5c{{m}^{2}}}=30\frac{l}{\min c{{m}^{2}}}$

Sin embargo la velocidad la debemos expresar en m/s, entonces aplicamos nuestros factores de conversión que serán los siguientes:

$\displaystyle \begin{array}{l}1l=1000c{{m}^{3}}\\1\min =60s\\1m=100cm\end{array}$

Aplicando:

$\displaystyle {{v}_{2}}=30\frac{l}{\min c{{m}^{2}}}\left( \frac{1\min }{60s} \right)\left( \frac{1000c{{m}^{3}}}{1l} \right)\left( \frac{1m}{100cm} \right)=5\frac{m}{s}$

Por lo que la velocidad final del chorro de agua es de 5 m/s

Resultado:

$\displaystyle {{v}_{2}}=5\frac{m}{s}$

1 Comentarios Publicados

Carlos Humberto Hernández Flórez dice:

14 febrero, 2023 a las 4:11 am

Excelente y muy buen material. Lo he compartido en clase con mis muchachos. Gracias.

Responder

Deja una respuesta Cancelar la respuesta