Gasto y Flujo - Ejercicios Resueltos

El día de hoy hablaremos sobre el gasto y flujo un tema muy útil en la hidrodinámica aquella área de la física que estudia la hidráulica y que se encarga de estudiar a los fenómenos de los líquidos en movimiento, y pone en evidencia aportes grandes como el diseño de canales, puertos, presas, hélices, turbinas, etc. Así que para entender éste tema solamente necesitas leer bien, entender la teoría y resolver ejercicios 😀

Hay que considerar algunos puntos importantes en el estudio de la hidrodinámica, antes de continuar:

1.- Los líquidos en su totalidad no son compresibles (no se pueden comprimir).

2.- Debemos considerar despreciable a la viscosidad, recordando qué estos principios son ideales, por lo que evitaremos la resistencia al flujo, así como omitir las pérdidas de energía mecánica producidas por la viscosidad.

3.- El flujo debe suponerse estacionario o estable. Ya que esto ocurre cuando la magnitud de la velocidad de toda partícula del líquido es similar al pasar por el mismo punto.

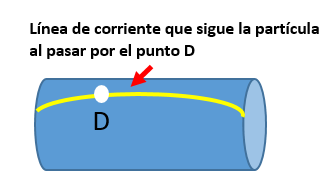
🤔 ¿A qué le llamamos Gasto?

Bien, el gasto es un concepto en física que advierte que cuando un líquido fluye a través de cierta tubería hay una relación entre el volumen del líquido y el tiempo que éste tarda en fluir.

Para ello veamos su fórmula:

$\displaystyle G=\frac{V}{t}$

Dónde:

G = gasto en $\displaystyle \frac{{{m}^{3}}}{s}$

V = volumen del líquido que fluye en metros cúbicos $\displaystyle {{m}^{3}}$

t = tiempo que tarda en fluir el líquido en segundos (s)

Bien, pero no es la única fórmula para poder obtener el gasto, existe otra fórmula que relaciona la magnitud de la velocidad del líquido y el área de la sección transversal de la tubería.

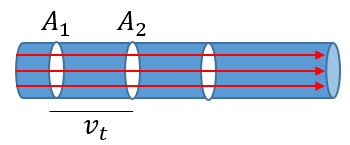
Para conocer por ejemplo el volumen de líquido que pasa de la primera sección de área a la segunda sección, basta con multiplicar el área, la magnitud de la velocidad del líquido y el tiempo que tarda en pasar por los puntos. Muy fácil ¿no? 😎

$\displaystyle V=Avt$

De ésta misma fórmula podemos obtener la segunda fórmula de la que hemos hablado.

$\displaystyle G=\frac{Avt}{t}=Av$

Dónde

G = gasto en $\displaystyle \frac{{{m}^{3}}}{s}$

A = área de la sección transversal de la tubería, medida en metros cuadrados.

v = magnitud de la velocidad del líquido en m/s

🔸 Fórmula del Gasto

En resumen, las dos fórmulas del gasto son:

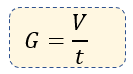
Otra forma de ver al gasto, es en términos del área por la velocidad.

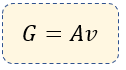
🤔 ¿Qué es el flujo?

Bien, así como vimos el concepto del gasto, el flujo no es más que la cantidad de masa del líquido que fluye a través de una tubería en unidad de tiempo.

Dada por la siguiente fórmula:

$\displaystyle F=\frac{m}{t}$

Dónde:

F = flujo en kg/s

m = masa del líquido en unidades de kg (kilogramos)

t = tiempo que tarda en fluir en segundos (s)

Bien, pero así como el gasto, existe otra fórmula derivada de la densidad que nos permite obtener el flujo.

Como sabemos, la densidad de un cuerpo es la relación entra la masa y volumen, entonces obtenemos:

$\displaystyle \rho =\frac{m}{V}$

Despejando a la "masa"

$\displaystyle m=\rho V$

Entonces de la ecuación que tenemos de flujo, reemplazamos a la "masa" por la nueva forma de la densidad.

$\displaystyle F=\frac{\rho V}{t}$

Pero la podemos dejar en términos del Gasto, ya que el gasto es:

$\displaystyle G=\frac{V}{t}$

Entonces:

$\displaystyle F=G\rho $

Dónde el Gasto por la densidad nos da el flujo.

🔸 Fórmulas del Flujo

En resumen, las dos fórmulas del flujo son:

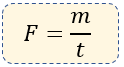
Otra forma de ver la fórmula del flujo, es en términos del gasto por el producto de la densidad.

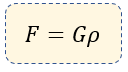
Ejercicios Resueltos de Gasto y Flujo

Para empezar a entender los siguientes ejemplos de gasto y flujo, es importante repasar los ejercicios por tu cuenta, y así evitar problemas de comprensión. 😊

Solución: Lo primero que haremos será analizar nuestros datos:

G = ?

V = $\displaystyle 1.8{{m}^{3}}$

t = $\displaystyle 0.5\min \left( \frac{60s}{1\min } \right)=30s$

Aplicando la fórmula de Gasto:

$\displaystyle G=\frac{1.8{{m}^{3}}}{30s}=0.06\frac{{{m}^{3}}}{s}$

Solución: 

Coloquemos nuestros datos:

t = ?

V = 8 m^3

G = 60 l/s

No podemos manejar el gasto con unidades de (litro/segundo) , por lo que debemos de convertir esos litros a metros cúbicos, el factor de conversión es 1 metro cúbico = 1000 litros.

$\displaystyle G=60\frac{l}{s}\left( \frac{1{{m}^{3}}}{1000l} \right)=0.06\frac{{{m}^{3}}}{s}$

Una vez teniendo el Gasto en las unidades del SI (Sistema Internacional), ahora es momento de ver la fórmula a utilizar:

$\displaystyle G=\frac{V}{t}$

Despejando al tiempo "t"

$\displaystyle t=\frac{V}{G}$

Sustituyendo

$\displaystyle t=\frac{V}{G}=\frac{8{{m}^{3}}}{0.06\frac{{{m}^{3}}}{s}}=133.33s$

Algo aproximado a los 2 minutos con 22 segundos 😀

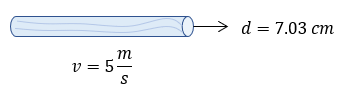
Solución: Bien, este problema requiere de un análisis más minucioso a los ejercicios anteriores, pero partamos de nuestros datos:

d = ?

G = 0.5 m^3/s

v = 6 m/s

Hay una fórmula del gasto que menciona la relación entre la velocidad y el área, por lo que usaremos esa:

$\displaystyle G=vA$

Vamos a despejar al "área" ya que de ahí podremos calcular el diámetro circular de la tubería.

$\displaystyle A=\frac{G}{v}$

Sustituyendo datos en la fórmula:

$\displaystyle A=\frac{G}{v}=\frac{0.5\frac{{{m}^{3}}}{s}}{6\frac{m}{s}}=0.0833{{m}^{2}}$

Pero si nos referimos al área de un círculo, sabemos que:

$\displaystyle A=\frac{\pi {{d}^{2}}}{4}$

Despejando al "diámetro"

$\displaystyle d=\sqrt{\frac{4A}{\pi }}$

Ahora es momento de obtener el diámetro en la fórmula:

$\displaystyle d=\sqrt{\frac{4\left( 0.0833 \right)}{\pi }}=0.326m$

Lo que nos da un diámetro de 0.326 metros.

a) El gasto

b) El flujo

Dato: densidad del agua 1000 kg/m^3

Solución:

 Bien, lo primero es tomar los datos que nos aporta el problema, así que:

G = ?

F = ?

V = 2300 litros

t = 1 minuto = 60 segundos

Necesitamos convertir los 2300 litros a metros cúbicos, para ello recurrimos a nuestro factor de conversión.

$\displaystyle V=2300l\left( \frac{1{{m}^{3}}}{1000l} \right)=2.3{{m}^{3}}$

Ahora si podemos calcular el gasto:

$\displaystyle G=\frac{2.3{{m}^{3}}}{60s}=0.0383\frac{{{m}^{3}}}{s}$

Teniendo el gasto, pasemos a calcular el flujo, que es el producto del gasto por la densidad del líquido.

$\displaystyle F=G\rho =(0.0383\frac{{{m}^{3}}}{s})(1000\frac{kg}{{{m}^{3}}})=38.3\frac{kg}{s}$

Lo que equivale a tener 38.3 kilogramos de agua por cada segundo.

📃 Ejercicios para Practicar de Gasto y Flujo

Veamos ahora algunos ejemplos para practicar con su respectiva solución paso a paso. Es importante comprobar sus resultados 😊👇

👉 Ver Solución

👉 Ver Solución

👉 Ver Solución