Principio de Arquimedes - Ejercicios Resueltos

Sin duda, el principio de Arquímedes es una gran herramienta en la física, principalmente en el área de la hidráulica, nos aporta un gran valor y conocimiento para entender por ejemplo la flotación de los cuerpos, otros conceptos y quizá hasta encontrar la respuesta que derivan de éste descubrimiento como el, ¿por qué flotan los barcos en el mar?, entonces, haciendo mención a ello, vamos a explicar la teoría y después como es costumbre pasaremos a ver problemas resueltos sobre éste principio. 😎
Comprendiendo el Teorema de Arquímedes
Si te has dado cuenta, cuando un cuerpo es sumergido en un líquido, éste cuerpo ejerce una presión vertical ascendente (como si empujara para no ser sumergido), puedes experimentarlo con una pelota en un estanque, o en la alberca.
Pues bien el empuje que reciben los cuerpos al ser introducidos en un líquido fue la investigación que nos aportó el gran genio de la antigua Grecia el gran Arquímedes, además de ser un hombre destacado también exploró en otros fenómenos tales como las palancas, la geometría plana y del espacio, y su teoría sobre los números.

En la imagen de arriba podemos ver un claro ejemplo de la resistencia que hará la pelota al ser sumergida, hará un empuje hacía arriba. 😀
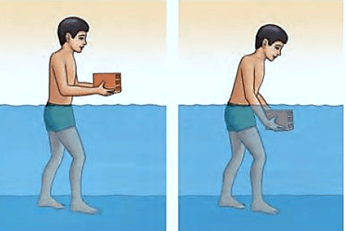
En la imagen del niño con un bloque puede ser explicado de la siguiente manera, si mantiene un objeto suspendido fuera y dentro del agua, va a comprobar que dentro del agua el bloque parece más ligero. ¿cierto?
El principio de Arquímedes estipula lo siguiente:
Para el principio de Arquímedes tenemos varios casos, de acuerdo a la magnitud de dos fuerzas que son el peso que lo empuja hacía abajo, y el empuje del líquido que lo impulsa hacia arriba. Hablando de un cuerpo sumergido.
Casos del Principio de Arquimedes
1.- Si la magnitud del peso del cuerpo es menor a la magnitud de empuje.
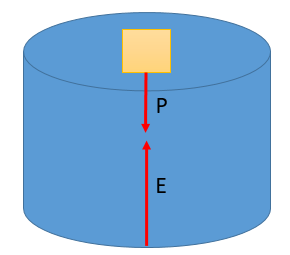
Para el primer caso, podemos tener que la magnitud del peso del cuerpo sea menor a la magnitud del empuje que recibe, flota porque desaloja la menor cantidad del líquido que su volumen.
2.- Si la magnitud del peso es igual a la magnitud de empuje
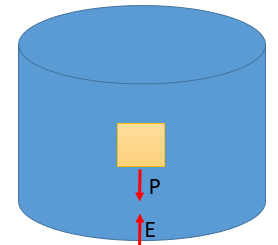
Como segundo caso tenemos, que la magnitud del peso del cuerpo sea igual a la magnitud del empuje que recibe, esto hará que el cuerpo permanezca en equilibrio, o lo que hace alusión a tener el cuerpo sumergido dentro del líquido.
3.- Si la magnitud del peso del cuerpo es mayor que la magnitud del empuje
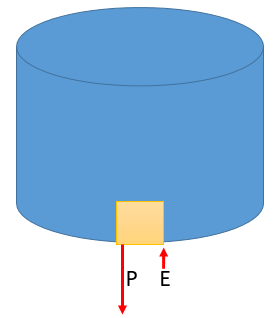
Aquí es el caso cuando experimentamos que el cuerpo se hunde. O sea como el enunciado lo menciona, la magnitud del peso del cuerpo es mayor a la magnitud del empuje, y lógicamente al estar completamente sumergido el cuerpo desalojará un volumen del líquido igual a su volumen.
Podemos con esto respondernos que para que un barco flote debe desalojar un volumen de líquido cuyo peso sea igual al del barco.
Fórmula del Principio de Arquímedes
La fórmula del principio o teorema de arquímedes es muy sencilla, está dada de la siguiente manera:
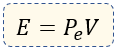
Dónde:
E = Empuje (se mide en Newtons)
Pe = Peso Específico (Se mide en Newtons/m³)
V = Volumen (se mide en m³)
Es importante que al observar que en la fórmula del empuje vemos al peso específico, entonces podemos escribir la fórmula también de la siguiente manera:
![]()
Dónde:
E = Empuje (se mide en Newtons)
ρ = Densidad (se mide en Kg/m³)
g = Gravedad (Se mide en m/s²)
V = Volumen (se mide en m³)
▶ Ejercicios Resueltos del Principio de Arquímedes
Bien ahora que sabemos muy bien el tema de la densidad de algunos cuerpos, y conocemos la teoría básica del principio de flotabilidad, podemos decir que:
Para que un cuerpo flote en cualquier fluido, su densidad promedio debe ser menor a la del fluido.
Esto tiene por fórmula:
$\displaystyle E={{P}_{e}}V$
Ahora si pasemos a los ejemplos resueltos.
Solución:
Lo primero que haremos será considerar los datos y empezar a sustituir en las fórmulas que tengamos a disposición. Recordemos que para calcular el empuje, es necesario tener el volumen y el peso específico. Para calcular el volumen basta primero en convertir las unidades de la arista a metros (SI) unidades del Sistema Internacional.
Datos:
$\displaystyle l=20cm\left( \frac{1m}{100cm} \right)=0.2m$
$\displaystyle P=560.4N$
$\displaystyle V=(0.2m)(0.2m)(0.2m)=8x{{10}^{-3}}{{m}^{3}}$
El peso específico del agua es:
$\displaystyle {{P}_{e}}\left( {{H}_{2}}O \right)=9800\frac{N}{{{m}^{3}}}$
Ahora si podemos comenzar a resolver.
- a) Calculando el Empuje
$\displaystyle E={{P}_{e}}V=(9800\frac{N}{{{m}^{3}}})(8x{{10}^{-3}}{{m}^{3}})=78.4N$
- b) Calculando el Peso Aparente
$\displaystyle {{P}_{aparente}}={{P}_{real}}-Empuje$
$\displaystyle {{P}_{aparente}}=560.4N-78.4N=482N$
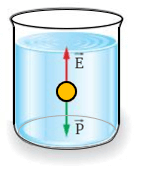
Solución:
El problema nos proporcionan datos muy importantes para colocarlos en nuestra fórmula de empuje, pues contamos con el volumen, la densidad del líquido donde se sumerge dicha esfera y además de forma implícita sabemos qué la gravedad es una constante de 9.8 m/s²
- a) Calculando la intensidad de empuje en la esfera
Si en los datos tenemos a la gravedad y a la densidad podemos aplicar entonces:
$\displaystyle E=\rho gV$
Si sustituimos nuestros datos en la fórmula, obtenemos:
$\displaystyle E=\rho gV=\left( 900\frac{kg}{{{m}^{3}}} \right)\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 3x{{10}^{-4}}{{m}^{3}} \right)=2.646N$
Un empuje de 2.646 Newtons.
- b) Calculando la intensidad del peso de la esfera para que se desplace tanto hacía arriba o hacía abajo
No necesitamos hacer prácticamente ningún cálculo, solo analizar lo que hemos encontrado en el inciso a. Por ejemplo:
Si el Peso de la esfera es mayor al empuje, entonces:
$\displaystyle {{P}_{esfera}}>E$
Se desplazará hacia abajo.
Si el Peso de la esfera es menor al empuje, entonces:
$\displaystyle {{P}_{esfera}}<E$
Se desplazará hacía arriba.
Ejercicios para Practicar del Principio de Arquímedes
Veamos los siguientes ejercicios para practicar el tema del teorema de arquímedes. Recuerde dar click en "ver solución" para analizar paso a paso los resultados:
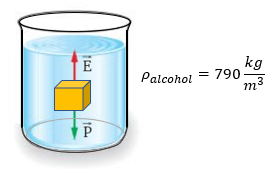
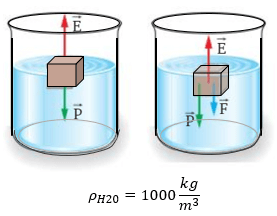
Examen del Principio de Arquímedes
Ahora es momento de practicar, resuelve el siguiente examen con 10 preguntas sobre el tema del principio de Arquímedes.
Cargando examen...
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Me sirvio muchisimo, gracias
★★★★★
71 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar