Densidad y Peso Especifico - Ejercicios Resueltos

¿Qué tal? Hoy tenemos un tema muy entretenido en Física, especialmente del área de la hidráulica, y es que se trata de la densidad y peso especifico, uno de los temas que nos aporta muchísimo valor en el campo de los fluidos. 😎

Contenidos

1 Viscosidad, Tensión Superficial, Cohesión, Adherencia y Capilaridad
2 🔹 ¿Qué es la Densidad?
3 🔸 ¿Qué es el Peso Específico?
4 Tabla de valores de Densidad y Peso Específico
5 Ejercicios Resueltos de Densidad y Peso Especifico
6 📃 Problemas para Practicar de Densidad y Peso Específico

Viscosidad, Tensión Superficial, Cohesión, Adherencia y Capilaridad

No olvidemos que dentro del tema de la hidráulica hay muchos conceptos que debemos de tener en cuenta antes de abordar cualquier tema relacionado a este campo, por ejemplo las siguientes definiciones que conforman a la Hidráulica en sí. Los líquidos poseen características tales como la viscosidad, tensión superficial, cohesión, adherencia y capilaridad. Y cada una de ellas
se originan y presentan de diversas formas. Por ejemplo:

La viscosidad se da por el rozamiento de unas partículas con otras, cuando el líquido fluye; la tensión superficial se presenta debido a la atracción entre algunas moléculas del líquido por lo que la superficie libre de cualquier líquido se comporta como una finísima membrana elástica, ahora con la cohesión; la cohesión no es más que la fuerza que mantiene unidas a las moléculas de una misma sustancia, a diferencia de la adherencia que es la fuerza de atracción que se manifiesta en moléculas de dos sustancias diferentes, y finalmente tenemos a la capilaridad que se presenta cuando existe contacto entre un líquido y una pared sólida, especialmente si son tubos muy delgados, llamados capilares.

🔹 ¿Qué es la Densidad?

La densidad de una sustancia, también llamada por algunos autores como la “masa específica“, es una propiedad de la materia que expresa a la masa contenida por unidad de volumen. Su fórmula es:

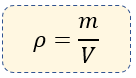
$\displaystyle \rho =\frac{m}{V}$

Donde la letra “ρ” RO Griega simboliza a la densidad, Sus unidades en el SI (Sistema Internacional), son en kg/m³ (kilogramo sobre metro cúbico).

Por otro lado:

🔸 ¿Qué es el Peso Específico?

El peso específico de una sustancia es también una propiedad característica; su valor está determinando por el cociente entre el peso por unidad de volumen, matemáticamente esto es:

$\displaystyle {{P}_{e}}=\frac{P}{V}$

Dónde:

Pe = Peso específico (N/m^3) “Newton sobre metro cúbico”

P = Peso de la sustancia en Newtons (N).

V = Volumen que ocupa la sustancia en metro cúbicos (m^3).

Bien, ahora veamos algunos ajustes matemáticos que podemos realizar para obtener fórmulas nuevas a través de las que ya tenemos. Por ejemplo, recordemos que el peso es igual a la masa por gravedad, o sea.

$\displaystyle P=mg$

Como sabemos que el peso específico es Peso sobre Volumen, sustituyamos el Peso de masa por gravedad en la fórmula de peso específico.

$\displaystyle {{P}_{e}}=\frac{P}{V}=\frac{mg}{V}$

Pero recordemos que la densidad es igual a masa sobre volumen, entonces podemos simplificar la fórmula:

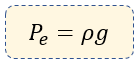
$\displaystyle {{P}_{e}}=\frac{P}{V}=\frac{mg}{V}=\rho g$

Por lo que ya tenemos nueva fórmula para calcular el peso especifico.

Tabla de valores de Densidad y Peso Específico

Aquí se ilustran algunos valores de densidad y peso específico que nos serán de gran utilidad para la resolución de problemas.

Sustancia	Densidad (Kg/m³)	Peso Específico (N/m³)
Agua (4° C)	1000	9,800
Alcohol	790	7,742
Aceite	915	8,967
Hielo	920	9,016
Madera	430	4,214
Oro	19,320	189,336
Hierro	7,860	77,028
Mercurio	13,600	13,280
Oxigeno (0°)	1.43	14.014
Hidrógeno (0°)	0.09	0.882

Ejercicios Resueltos de Densidad y Peso Especifico

Bien, ahora es momento de practicar, de poner en práctica parte de la teoría aquí aprendida.

Tomar en cuenta algunos factores de conversión que podamos usar dentro de los ejercicios aquí propuestos:

1000 gramos = 1 Kilogramo

1000000 centímetros cúbicos = 1 metro cúbico

Problema 1.-Un cuerpo sólido de cierto material, se midió su masa y se encontró un valor de 700 gramos; al medir su volumen éste fue de 2,587 centímetros cúbicos. Calcular la densidad en el SI (Sistema Internacional).

Solución: En este ejemplo, tenemos el dato de la masa de 700 gramos de hierro, y a su vez un volumen de 2587 centímetros cúbicos, entonces nuestros datos no están en el sistema internacional, por lo que haremos una sencilla conversión.

Datos:

$\displaystyle m=700g\left( \frac{1kg}{1000g} \right)=0.7kg$

$\displaystyle V=2587c{{m}^{3}}\left( \frac{1{{m}^{3}}}{1000000c{{m}^{3}}} \right)=2.587x{{10}^{-3}}{{m}^{3}}$

Aplicando la fórmula.

$\displaystyle \rho =\frac{0.7kg}{2.587x{{10}^{-3}}{{m}^{3}}}=270.58\frac{kg}{{{m}^{3}}}$

Qué sería la densidad de dicho material.

Problema 2.- 0.5 kg de alcohol etílico ocupan un volumen de 0.000544 metros cúbicos. Calcular:

a) ¿La densidad del alcohol etílico?

b) ¿Cuál es su peso específico?

Solución: Este problema nos aporta la mayor cantidad de datos que necesitamos para poder calcular.

$\displaystyle \rho =\frac{0.5kg}{0.000544{{m}^{3}}}=919.118\frac{kg}{{{m}^{3}}}$

Ahora veamos el peso específico

$\displaystyle {{P}_{e}}=\left( 919.118\frac{kg}{{{m}^{3}}} \right)(9.8\frac{m}{{{s}^{2}}})=9007.35\frac{N}{{{m}^{3}}}$

Problema 3. Calcular la masa y el peso de 14500 litros de gasolina. Si la densidad de la gasolina es de 700 kg/m^3.

Solución: Este problema nos advierte sobre el peso de la gasolina, y su densidad, por lo que solo tendremos que buscar la fórmula correspondiente y resolver.

Por la fórmula de densidad, podemos hacer el despeje de la variable masa, quedando así:

$\displaystyle m=\rho V$

Sin embargo, no podemos colocar el volumen todavía porque tendríamos que hacer nuestra conversión de litros a metros cúbicos. Para ello:

$\displaystyle 14500l\left( \frac{1{{m}^{3}}}{1000l} \right)=14.5{{m}^{3}}$

Ahora si podemos aplicar la fórmula de la masa:

$\displaystyle m=\left( 700\frac{kg}{{{m}^{3}}} \right)\left( 14.5{{m}^{3}} \right)=10150kg$

y para calcular el peso. Solamente multiplicamos por la gravedad.

$\displaystyle P=(10150kg)(9.8\frac{m}{{{s}^{2}}})=99470N$

Problema 4.- ¿Cuál es la densidad de un aceite cuyo peso específico es de 6578 N/m^3?

Solución: Es momento de anotar nuestros datos y observar que fórmula usaremos.

Sabemos que el peso específico la podemos expresar en función de la densidad de la siguiente forma:

$\displaystyle \rho =\frac{{{P}_{e}}}{g}=\frac{6578\frac{N}{{{m}^{3}}}}{9.8\frac{m}{{{s}^{2}}}}=671.22\frac{kg}{{{m}^{3}}}$

Con lo que damos con la densidad de dicho aceite.

📃 Problemas para Practicar de Densidad y Peso Específico

Colocaremos algunos problemas para que los resuelvas con calma en tu libreta, y así también podrás corroborar tus resultados, los ejercicios están resueltos paso a paso. Dar click en “Ver Solución”. 👇😊

Problema 5. Calcular el peso específico del oro cuya densidad es de 19300 kg/m^3

👉 Ver Solución

Problema 6. ¿Qué volumen debe tener un tanque para que pueda almacenar 3040 kg de gasolina cuya densidad es de 680 kg/m^3?

👉 Ver Solución

Problema 7. Calcular la densidad de un prisma rectangular cuyas dimensiones son: largo 6cm, ancho 5 cm, alto 3 cm, y tiene una masa de 300 g; calcular el volumen que ocupará un objeto de la misma sustancia si tiene una masa de 100 g.