Solución Problema 3 de Gasto y Flujo

Con este último problema de Gasto y Flujo , el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula de Gasto y Flujo y que resuelve todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐

Solución:

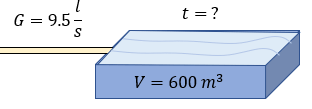
Este problema puede parece un poco complicado o complejo, pero realmente no lo es. El problema nos pide encontrar el tiempo que tarda en llenarse una alberca, nos dan datos como el volumen y también el gasto. Al tener tanto al volumen como al gasto, es lógico que el tiempo se puede obtener de manera directa, con la fórmula principal del gasto. Entonces procedemos a calcular.

• Obtener el tiempo que tarda en llenarse la alberca

Datos:

$latex \displaystyle G=9.5\frac{l}{s}$

$latex \displaystyle V=600{{m}^{3}}$

a) Obteniendo el tiempo

Antes de obtener el tiempo, podemos convertir los 600 m³ en litros o incluso podemos hacerlo al revés, convertir los 9.5 l/s a m³. No importa como lo hagamos el resultado tiene que ser el mismo, por comodidad convertiremos los 600 m³ a litros.

$latex \displaystyle V=600{{m}^{3}}\left( \frac{1000l}{1{{m}^{3}}} \right)=600000$

Es una alberca que le caben exactamente 600 mil litros. Ahora pasemos a aplicar nuestra fórmula:

$latex \displaystyle G=\frac{V}{t}$

Despejamos al "tiempo"

$latex \displaystyle t=\frac{V}{G}$

Sustituimos nuestros datos en la fórmula:

$latex \displaystyle t=\frac{V}{G}=\frac{600000l}{9.5\frac{l}{s}}=63157.89s$

Sin embargo el problema nos pide encontrar el tiempo en minutos y horas, aplicamos la (Conversión de Unidades).

$latex \displaystyle t=\left( 63157.89s \right)\left( \frac{1\min }{60s} \right)=1052.6315\min $

El tiempo en minutos es de 1052.6315 minutos

Ahora lo convertimos a horas.

$latex \displaystyle t=1052.6315\min \left( \frac{1hr}{60\min } \right)=17.54hr$

Es decir 17.54 horas

Resultado:

$latex \displaystyle t=1052.6315\min =17.54hr$