Módulo Volumétrico - Ejercicios Resueltos
Avanzamos en nuestra serie sobre elasticidad. Ya hemos diseccionado cómo los materiales responden a fuerzas de tracción y compresión a través del Módulo de Young ($E$), y cómo resisten cambios de forma bajo cizalladura mediante el Módulo de Corte ($G$). Ahora, exploraremos cómo los materiales (tanto sólidos como fluidos) se comportan cuando son sometidos a una presión uniforme desde todas las direcciones. Esta propiedad se cuantifica mediante el Módulo Volumétrico ($K$).
Introducción
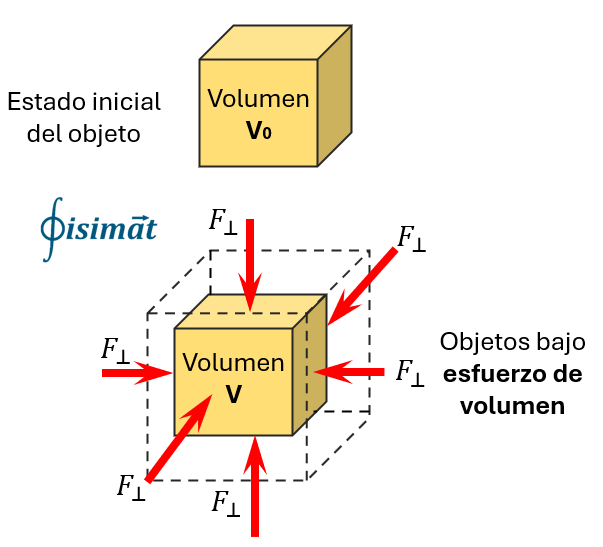
El Módulo Volumétrico ($K$), también conocido como Módulo de Compresibilidad Volumétrica, es una medida de la resistencia de un material a la compresión uniforme. Describe cuánto se comprimirá un material, es decir, cuánto disminuirá su volumen, cuando se le somete a una presión externa desde todas las direcciones. A diferencia del Módulo de Young (que se enfoca en la deformación en una dirección) y del Módulo de Corte (que se enfoca en la distorsión de la forma), el Módulo Volumétrico se refiere exclusivamente al cambio de volumen sin cambio de forma.
Este concepto es de vital importancia no solo para los sólidos, sino especialmente para la mecánica de fluidos (líquidos y gases). Permite entender por qué consideramos a los líquidos como "incompresibles" en muchas aplicaciones hidráulicas y cómo la presión afecta la densidad de los gases. Además, el Módulo Volumétrico es fundamental en campos como la geofísica, para estudiar la propagación de ondas sísmicas a través del interior de la Tierra, y en la acústica, para determinar la velocidad del sonido en diferentes medios. 🤓
Definición del Módulo Volumétrico ($K$)
La definición del Módulo Volumétrico se basa en la relación entre el cambio de presión aplicado a un cuerpo y el cambio de volumen resultante.
Esfuerzo Volumétrico (Presión) y Deformación Unitaria Volumétrica
Recordemos brevemente los conceptos clave:
- El esfuerzo volumétrico es simplemente la presión ($P$) que actúa uniformemente sobre toda la superficie de un cuerpo. Un cambio en este esfuerzo se denota como $\Delta P$.
- La deformación unitaria volumétrica ($\epsilon_V$) es el cambio fraccional en el volumen, definido como el cambio de volumen ($\Delta V$) dividido por el volumen original ($V_0$):
$$\epsilon_V = \frac{\Delta V}{V_0}$$
Un $\Delta V$ negativo indica una disminución de volumen.
El Módulo Volumétrico como Medida de Incompresibilidad
Para un material elástico, un aumento en la presión externa ($\Delta P > 0$) provoca una disminución en el volumen ($\Delta V < 0$). La relación entre el cambio de presión y la deformación unitaria volumétrica es lineal dentro del límite elástico. El Módulo Volumétrico ($K$) se define como:
$$K = - \frac{\Delta P}{\epsilon_V} = - \frac{\text{Cambio de Presión}}{\text{Deformación Unitaria Volumétrica}}$$
Sustituyendo la definición de $\epsilon_V$, obtenemos la fórmula completa:
$$K = - \frac{\Delta P}{(\Delta V / V_0)}$$
[alert-warning] El signo negativo es crucial: asegura que el Módulo Volumétrico $K$ sea siempre un valor positivo. Si la presión aumenta ($\Delta P$ es positivo), el volumen disminuye ($\Delta V$ es negativo), y el signo negativo en la fórmula cancela este efecto, resultando en un $K$ positivo. Un valor alto de $K$ indica que el material es muy resistente a la compresión (casi incompresible). [/alert-warning]
[alert-note] Ejemplo Un aumento de presión de $20 \text{ MPa}$ sobre un bloque de cierto material causa que su volumen disminuya en un $0.1\%$. ¿Cuál es su Módulo Volumétrico? [/alert-note]
Respuesta:
El cambio de presión es $\Delta P = 20 \text{ MPa} = 20 \times 10^6 \text{ Pa}$.
La deformación volumétrica es una disminución del $0.1\%$, por lo que $\epsilon_V = -0.1 / 100 = -0.001$.
$K = - \frac{\Delta P}{\epsilon_V} = - \frac{20 \times 10^6 \text{ Pa}}{-0.001} = 20 \times 10^9 \text{ Pa} = 20 \text{ GPa}$.
Compresibilidad ($\beta$)
La compresibilidad ($\beta$ o $k$) es simplemente el inverso del Módulo Volumétrico. Es una medida de la facilidad con la que un volumen puede ser reducido bajo presión.
$$\beta = \frac{1}{K} = - \frac{1}{V_0} \frac{\Delta V}{\Delta P}$$
Un material con alta compresibilidad ($\beta$ grande) es fácil de comprimir (por ejemplo, un gas), lo que corresponde a un Módulo Volumétrico ($K$) bajo. Sus unidades en el SI son $Pa^{-1}$.
[alert-note] Ejemplo El agua tiene un Módulo Volumétrico de aproximadamente $K = 2.2 \text{ GPa}$. Calcula su compresibilidad. [/alert-note]
Solución:
$K = 2.2 \times 10^9 \text{ Pa}$.
$\beta = \frac{1}{K} = \frac{1}{2.2 \times 10^9 \text{ Pa}} \approx 0.455 \times 10^{-9} \text{ Pa}^{-1}$.
Este valor tan pequeño indica que el agua es muy poco compresible.
Módulo Volumétrico en Diferentes Estados de la Materia
El Módulo Volumétrico varía drásticamente entre sólidos, líquidos y gases.
Sólidos y Líquidos
Tanto los sólidos como los líquidos tienen valores de Módulo Volumétrico muy altos, lo que significa que son casi incompresibles. Para cambiar su volumen de manera significativa se requieren presiones extremadamente altas. Esta propiedad es el fundamento de los sistemas hidráulicos: como el líquido no se comprime fácilmente, la presión aplicada en un punto se transmite eficientemente a otro punto para realizar trabajo (Principio de Pascal).
Gases
Los gases, a diferencia de los sólidos y líquidos, son altamente compresibles. Tienen valores de Módulo Volumétrico muy bajos. El $K$ de un gas no es constante, sino que depende de las condiciones del proceso de compresión. Por ejemplo, para un gas ideal a presión $P$, el módulo volumétrico isotérmico (a temperatura constante) es simplemente $K_{isotérmico} = P$.
Valores Típicos
📝 Nota: Estos son valores aproximados del módulo volumétrico \( K \), expresados en gigapascales (GPa). Pueden variar según la temperatura, presión y pureza del material.
| Material | Estado | Módulo Volumétrico \( K \) (GPa) |
|---|---|---|
| Acero | Sólido | \( K \approx 160 \, \text{GPa} \) |
| Aluminio | Sólido | \( K \approx 75 \, \text{GPa} \) |
| Vidrio | Sólido | \( K \approx 40 \, \text{GPa} \) |
| Agua | Líquido | \( K \approx 2.2 \, \text{GPa} \) |
| Glicerina | Líquido | \( K \approx 4.5 \, \text{GPa} \) |
| Aire | Gas (a 1 atm, isotérmico) | \( K \approx 0.000101 \, \text{GPa} \) |
Aplicaciones del Módulo Volumétrico
El Módulo Volumétrico es un parámetro clave en muchas áreas científicas y tecnológicas.
Mecánica de Fluidos e Hidráulica
Como se mencionó, el alto valor de $K$ para los líquidos justifica la suposición de incompresibilidad en muchos análisis de flujo de fluidos y es fundamental para el funcionamiento de frenos, prensas y actuadores hidráulicos.
Geofísica y Sismología
La velocidad de las ondas de compresión (ondas P), que son las ondas sísmicas más rápidas, depende tanto del Módulo Volumétrico como del Módulo de Corte del medio que atraviesan ($v_p = \sqrt{(K + \frac{4}{3}G)/\rho}$). Analizando cómo varía la velocidad de estas ondas al viajar por el interior del planeta, los geofísicos pueden inferir las propiedades elásticas y la composición del manto y el núcleo de la Tierra.
Acústica
La velocidad del sonido en un medio fluido (líquido o gas) está directamente relacionada con su Módulo Volumétrico y su densidad ($\rho$):
$$v = \sqrt{\frac{K}{\rho}}$$
Un medio más rígido (mayor $K$) y menos denso (menor $\rho$) permite una propagación más rápida del sonido.
[alert-note] Ejemplo Calcular la velocidad del sonido en el agua, usando $K_{agua} \approx 2.2 \text{ GPa}$ y $\rho_{agua} \approx 1000 \text{ kg/m}^3$. [/alert-note]
Solución:
$K = 2.2 \times 10^9 \text{ Pa}$. $\rho = 1000 \text{ kg/m}^3$.
$v = \sqrt{\frac{2.2 \times 10^9 \text{ N/m}^2}{1000 \text{ kg/m}^3}} = \sqrt{2.2 \times 10^6 \text{ m}^2/\text{s}^2} \approx 1483 \text{ m/s}$.
Este valor es muy cercano al valor medido experimentalmente para la velocidad del sonido en el agua.
Relación entre Módulos Elásticos para Materiales Isótropos
Para materiales isótropos, los módulos elásticos están interconectados. Conocer el Módulo Volumétrico nos permite completar el cuadro de estas relaciones.
La Conexión Completa: $E$, $G$, $K$ y $\nu$
Además de la relación $E = 2G(1+\nu)$ vista en el artículo anterior, existe otra ecuación que conecta el Módulo de Young ($E$), el Módulo Volumétrico ($K$) y el Coeficiente de Poisson ($\nu$):
$$E = 3K(1-2\nu)$$
Esta relación es muy importante porque impone una restricción teórica sobre el Coeficiente de Poisson. Dado que $E$ y $K$ son siempre positivos para cualquier material estable, el término $(1-2\nu)$ también debe ser positivo, lo que implica que $\nu < 0.5$.
Combinando estas ecuaciones, se puede obtener una fórmula que relaciona los tres módulos elásticos directamente:
$$E = \frac{9KG}{3K+G}$$
Esto demuestra que, para un material isótropo, solo dos de las constantes elásticas ($E$, $G$, $K$, $\nu$) son independientes. Si conocemos dos cualesquiera, podemos calcular las otras.
Ejercicios Resueltos de Módulo Volumétrico
Solución
▷ Paso 1 Identificar los datos.
$\Delta P = 50 \text{ MPa} = 50 \times 10^6 \text{ Pa}$.
El volumen se reduce en $0.025\%$, por lo que la deformación volumétrica es negativa:
$\epsilon_V = - \frac{0.025}{100} = -0.00025$.
▷ Paso 2 Aplicar la fórmula del Módulo Volumétrico.
$K = - \frac{\Delta P}{\epsilon_V} = - \frac{50 \times 10^6 \text{ Pa}}{-0.00025}$.
$K = \frac{50 \times 10^6 \text{ Pa}}{2.5 \times 10^{-4}} = \frac{50}{2.5} \times 10^{10} \text{ Pa} = 20 \times 10^{10} \text{ Pa}$.
▷ Paso 3 Expresar el resultado en GPa.
$K = 200 \text{ GPa}$.
Respuesta: El Módulo Volumétrico del metal es $200 \text{ GPa}$.
Solución
▷ Paso 1 Identificar el dato.
$K = 28.5 \text{ GPa} = 28.5 \times 10^9 \text{ Pa}$.
▷ Paso 2 Aplicar la fórmula de la compresibilidad $\beta = 1/K$.
$\beta = \frac{1}{28.5 \times 10^9 \text{ Pa}}$.
▷ Paso 3 Calcular el valor.
$\beta \approx 0.03508 \times 10^{-9} \text{ Pa}^{-1} = 3.508 \times 10^{-11} \text{ Pa}^{-1}$.
Respuesta: La compresibilidad del mercurio es aproximadamente $3.51 \times 10^{-11} \text{ Pa}^{-1}$.
Solución
▷ Paso 1 Identificar datos y convertir unidades a SI.
$V_0 = 1 \text{ L} = 0.001 \text{ m}^3$.
El volumen se comprime, por lo que el cambio de volumen es negativo:
$\Delta V = -1 \text{ cm}^3 = -1 \times (10^{-2} \text{ m})^3 = -1 \times 10^{-6} \text{ m}^3$.
$K = 2.2 \text{ GPa} = 2.2 \times 10^9 \text{ Pa}$.
▷ Paso 2 Reorganizar la fórmula $K = - \frac{\Delta P}{(\Delta V / V_0)}$ para despejar $\Delta P$.
$\Delta P = -K \left( \frac{\Delta V}{V_0} \right)$.
▷ Paso 3 Sustituir los valores y calcular $\Delta P$.
$\Delta P = -(2.2 \times 10^9 \text{ Pa}) \left( \frac{-1 \times 10^{-6} \text{ m}^3}{0.001 \text{ m}^3} \right)$.
$\Delta P = -(2.2 \times 10^9 \text{ Pa}) \left( \frac{-1 \times 10^{-6}}{1 \times 10^{-3}} \right)$.
$\Delta P = -(2.2 \times 10^9 \text{ Pa})(-1 \times 10^{-3}) = 2.2 \times 10^6 \text{ Pa}$.
▷ Paso 4 Expresar el resultado en MPa.
$\Delta P = 2.2 \text{ MPa}$.
Respuesta: Se necesita un cambio (aumento) de presión de $2.2 \text{ MPa}$.
Solución
▷ Paso 1 Calcular primero el Coeficiente de Poisson ($\nu$) usando la relación entre $E$ y $G$.
$E = 2G(1+\nu) \Rightarrow 1+\nu = \frac{E}{2G} \Rightarrow \nu = \frac{E}{2G} - 1$.
$\nu = \frac{70 \text{ GPa}}{2 \times 26 \text{ GPa}} - 1 = \frac{70}{52} - 1 \approx 1.346 - 1 = 0.346$.
▷ Paso 2 Usar la relación entre $E$, $K$ y $\nu$ para encontrar $K$.
$E = 3K(1-2\nu) \Rightarrow K = \frac{E}{3(1-2\nu)}$.
$K = \frac{70 \text{ GPa}}{3(1 - 2 \times 0.346)} = \frac{70 \text{ GPa}}{3(1 - 0.692)} = \frac{70 \text{ GPa}}{3(0.308)} = \frac{70 \text{ GPa}}{0.924}$.
▷ Paso 3 Calcular el valor de $K$.
$K \approx 75.76 \text{ GPa}$.
Respuesta: El Coeficiente de Poisson del aluminio es aproximadamente $0.346$ y su Módulo Volumétrico es aproximadamente $75.76 \text{ GPa}$.
Solución
▷ Paso 1 Identificar datos y convertir unidades si es necesario.
$K = 28.5 \text{ GPa} = 28.5 \times 10^9 \text{ Pa}$.
$\rho = 13600 \text{ kg/m}^3$.
▷ Paso 2 Aplicar la fórmula de la velocidad del sonido en un fluido $v = \sqrt{K/\rho}$.
$v = \sqrt{\frac{28.5 \times 10^9 \text{ Pa}}{13600 \text{ kg/m}^3}}$.
▷ Paso 3 Calcular el valor.
$v = \sqrt{2095588.2} \text{ m/s} \approx 1447.6 \text{ m/s}$.
Respuesta: La velocidad del sonido en el mercurio es aproximadamente $1448 \text{ m/s}$.
Solución
▷ Paso 1 Identificar datos.
$K = 140 \text{ GPa} = 140 \times 10^9 \text{ Pa}$.
$\Delta P = 280 \text{ MPa} = 280 \times 10^6 \text{ Pa}$.
▷ Paso 2 Despejar la deformación unitaria volumétrica ($\epsilon_V$) de la fórmula del Módulo Volumétrico.
$K = - \frac{\Delta P}{\epsilon_V} \Rightarrow \epsilon_V = -\frac{\Delta P}{K}$.
▷ Paso 3 Calcular $\epsilon_V$.
$\epsilon_V = -\frac{280 \times 10^6 \text{ Pa}}{140 \times 10^9 \text{ Pa}} = -\frac{280}{140000} = -0.002$.
▷ Paso 4 Expresar el resultado como un porcentaje.
La deformación unitaria es $-0.002$, lo que significa una disminución de $0.002$. Para convertir a porcentaje, multiplicamos por 100.
Porcentaje de disminución = $0.002 \times 100\% = 0.2\%$.
Respuesta: El volumen del bloque de cobre disminuirá en un $0.2\%$.
Solución
▷ Paso 1 Identificar los datos.
$E = 150 \text{ GPa}$.
$\nu = 0.25$.
▷ Paso 2 Usar la relación $E = 3K(1-2\nu)$ para despejar $K$.
$K = \frac{E}{3(1-2\nu)}$.
▷ Paso 3 Sustituir los valores y calcular.
$K = \frac{150 \text{ GPa}}{3(1 - 2 \times 0.25)} = \frac{150 \text{ GPa}}{3(1 - 0.5)} = \frac{150 \text{ GPa}}{3(0.5)} = \frac{150 \text{ GPa}}{1.5}$.
$K = 100 \text{ GPa}$.
Respuesta: El Módulo Volumétrico del material es $100 \text{ GPa}$.
Solución
▷ Paso 1 Calcular el cambio de presión ($\Delta P$) producido por la fuerza.
Área $A = 100 \text{ cm}^2 = 100 \times 10^{-4} \text{ m}^2 = 0.01 \text{ m}^2$.
Fuerza $F = 30 \text{ kN} = 30000 \text{ N}$.
$\Delta P = \frac{F}{A} = \frac{30000 \text{ N}}{0.01 \text{ m}^2} = 3,000,000 \text{ Pa} = 3 \text{ MPa}$.
▷ Paso 2 Identificar los otros datos.
$V_0 = 500 \text{ cm}^3 = 500 \times 10^{-6} \text{ m}^3 = 5 \times 10^{-4} \text{ m}^3$.
$K = 1.5 \text{ GPa} = 1.5 \times 10^9 \text{ Pa}$.
▷ Paso 3 Reorganizar la fórmula $K = - \frac{\Delta P}{(\Delta V / V_0)}$ para despejar $\Delta V$.
$\frac{\Delta V}{V_0} = -\frac{\Delta P}{K} \Rightarrow \Delta V = -V_0 \frac{\Delta P}{K}$.
▷ Paso 4 Sustituir los valores y calcular $\Delta V$.
$\Delta V = -(5 \times 10^{-4} \text{ m}^3) \frac{3 \times 10^6 \text{ Pa}}{1.5 \times 10^9 \text{ Pa}}$.
$\Delta V = -(5 \times 10^{-4} \text{ m}^3) \left( \frac{3}{1500} \right) = -(5 \times 10^{-4} \text{ m}^3) (0.002)$.
$\Delta V = -10 \times 10^{-7} \text{ m}^3 = -1 \times 10^{-6} \text{ m}^3$.
▷ Paso 5 (Opcional) Convertir el resultado a $cm^3$.
$1 \text{ m}^3 = (100 \text{ cm})^3 = 10^6 \text{ cm}^3$.
$\Delta V = -1 \times 10^{-6} \text{ m}^3 \times \frac{10^6 \text{ cm}^3}{1 \text{ m}^3} = -1 \text{ cm}^3$.
Respuesta: El cambio de volumen del aceite es una disminución de $1 \times 10^{-6} \text{ m}^3$, lo que equivale a $1 \text{ cm}^3$.
Conclusión
El Módulo Volumétrico ($K$) completa nuestra comprensión inicial de las constantes elásticas fundamentales al describir la resistencia de un material a cambiar su volumen bajo una presión uniforme. Hemos establecido que es una medida de incompresibilidad, con valores altos para sólidos y líquidos y bajos para gases. Su inverso, la compresibilidad, nos da una idea de cuán fácilmente se puede reducir el volumen de una sustancia.
Esta propiedad es crucial no solo en la mecánica de sólidos, sino también de manera prominente en la mecánica de fluidos, la acústica y la geofísica. Las relaciones matemáticas que conectan el Módulo Volumétrico con el Módulo de Young y el Módulo de Corte revelan la naturaleza interdependiente de las propiedades elásticas de los materiales isótropos. El último pilar conceptual que nos falta por explorar para tener una visión completa es el Coeficiente de Poisson, que será el tema de nuestro próximo artículo.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar