Presión - Ejercicios Resueltos

Hoy toca publicar un nuevo tema, y vamos a iniciar hablando sobre la presión y como actúa en algunos fluidos este fenómeno físico. Si bien la presión es aquella magnitud que mide la cantidad de fuerza que es aplicada a cierta área, también la vamos a leer en algunos textos formas de presión, como la presión atmosférica.

Donde la presión atmosférica es aquella presión donde la atmósfera ejerce en todas direcciones sobre los cuerpos que están dentro de ella, por ejemplo nosotros en la tierra. 😎

Mientras más alejados (altura) del nivel del mar estemos, menor será la cantidad de presión que ejerza la atmósfera sobre nosotros, a diferencia de que si estuviéramos cercanos al mar, donde la presión alcanzaría su máximo de:

$\displaystyle 1atm=760mmdeHg=1.013x{{10}^{5}}\frac{N}{{{m}^{2}}}$

Recordemos entonces:

Esto tiene por fórmula:

$\displaystyle P=\frac{F}{A}$

Dónde:

$\displaystyle P=presi\acute{o}n=\frac{N}{{{m}^{2}}}=Pascal=Pa$

$\displaystyle F=$ $ \displaystyle Fuerza=N$

$\displaystyle A=$ $ \displaystyle \acute{A}rea={{m}^{2}}$

En el siguiente vídeo podemos ver un claro ejemplo de la presión y la distribución del peso.

Lo podemos observar también de manera gráfica, con la siguiente imagen:

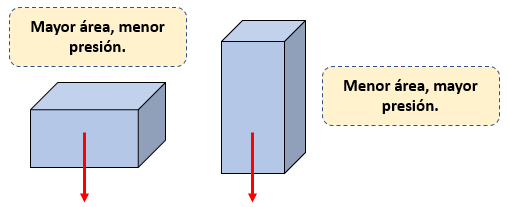
Ahora pasemos a ver unos ejemplos resueltos sobre este tema:

Ejemplos resueltos de Presión

Solución: Para ello vamos a tomar nuestros datos que el problema nos provee, por ejemplo nos da una fuerza de 120 N, y a su vez un área de 0.040 $ \displaystyle {{m}^{2}}$ , por lo que tenemos:

$\displaystyle F=120N$

$\displaystyle A=0.040{{m}^{2}}$

$\displaystyle P=$ ?

Reemplazando estos datos en nuestra fórmula tenemos:

Resultado: 

$\displaystyle P=\frac{F}{A}=\frac{120N}{0.040{{m}^{2}}}=3000Pa$

Por lo que obtenemos un total de 3000 pascales de presión ejercidas sobre la superficie.

Ahora compliquemos un poco más el problema y resolvamos el siguiente ejercicio.

Solución: En este caso tenemos nos hace falta encontrar una fuerza, puesto que no nos la proporciona el problema, sin embargo podemos hallarla de una manera muy sencilla. 🙂

Recordemos que la fuerza es igual al peso, entonces podemos calcular el peso de la persona mediante la siguiente fórmula:

$\displaystyle w=mg$

Es decir que el peso es el producto de la masa multiplicada por la gravedad y con ello obtendremos la fuerza que necesitamos, por lo que:

$\displaystyle w=(84kg)(9.81\frac{m}{{{s}^{2}}})=824.04N$

Ahora si podemos calcular la presión ejercida sobre la losa

Resultado: 

$\displaystyle P=\frac{F}{A}=\frac{824.04N}{225{{m}^{2}}}=3.6624Pa$

Podemos observar que no hay gran dificultad al resolver este tipo de ejercicios, veamos otro más.

Solución: En este caso nos pide hallar la fuerza que se ejerce sobre la ventana, para ello vamos a tomar nuestros datos:

$\displaystyle P=1x{{10}^{5}}Pa$

$\displaystyle A=(50cm)(75cm)=3750c{{m}^{2}}$

$\displaystyle F=$ ?

Antes de poder reemplazar en la fórmula nuestros datos, debemos recordar que el área no lo podemos trabajar con centímetros cuadrados, para ello debemos convertir esa área en metros cuadrados, aplicando el siguiente factor de conversión

$\displaystyle A=3750c{{m}^{2}}\left( \frac{1{{m}^{2}}}{10,000c{{m}^{2}}} \right)=0.375{{m}^{2}}$

Ahora si podemos reemplazar en nuestra fórmula

$\displaystyle P=\frac{F}{A}$

Solo que el problema nos pide la fuerza, no la presión... Entonces vamos a despejar a "F"

$\displaystyle F=P\cdot A$

Reemplazando datos

$\displaystyle F=(1x{{10}^{5}}pa)(0.375{{m}^{2}})=37500N$

O lo que es igual a

Resultado: 

$\displaystyle 37.5kN$ (Kilo Newtons)

Ahora veamos otro concepto de aplicación.

Prensa Hidráulica - Ejercicios Resueltos

Otro de los ejemplos que podemos encontrar sin duda, es sobre la prensa hidráulica: este dispositivo emplea el principio de Pascal para su funcionamiento, está formado por dos recipientes cilíndricos comunicados, estos recipientes contienen un fluido, la sección transversal de uno de ellos por lo general es mayor que el otro, cada recipiente tiene un émbolo.  😎

Si se ejerce una presión P1 en el émbolo más pequeño, se obtiene una presión P2 en el émbolo mayor, de tal forma que P1 = P2.

Entonces su fórmula sería:

$\displaystyle \frac{f}{a}=\frac{F}{A}$

Dónde:

$\displaystyle f=$ Fuerza aplicada en el émbolo menor [N ó Dinas]

$\displaystyle F=$ Fuerza en el émbolo menor [N ó Dinas]

$\displaystyle a=$ Área del émbolo menor [m^2 ó cm^2]

$\displaystyle A=$ Área del émbolo mayor [m^2 ó cm^2]

Ahora pasemos a ver un ejemplo:

Solución: Como en todos los problemas, debemos analizar nuestros datos primeramente porque a partir de ahí podemos saber que nos hace falta, como calcularlo y de alguna manera iniciar a resolver nuestro problema.

Tenemos que nuestro émbolo mayor tiene un diámetro de 40 cm, para ello lo primero que tenemos que hacer es convertir esos centímetros a metros, y hacer lo mismo con el émbolo menor.

$\displaystyle D=40cm\left( \frac{1m}{100cm} \right)=0.4m$

$\displaystyle d=2.3cm\left( \frac{1m}{100cm} \right)=0.023m$

Ahora calcular el área de esos émbolos (recordar que se tratan de émbolos circulares):

$\displaystyle A=\frac{\pi {{D}^{2}}}{4}=\frac{\pi {{(0.4m)}^{2}}}{4}=0.1256{{m}^{2}}$

$\displaystyle a=\frac{\pi {{d}^{2}}}{4}=\frac{\pi {{(0.023m)}^{2}}}{4}=0.00041{{m}^{2}}$

Ahora vamos a despejar de nuestra fórmula a $\displaystyle f$

$\displaystyle f=\frac{F\cdot a}{A}$

Quedando así

? Resultado: 

$\displaystyle f=\frac{(50,000N)\cdot (0.00041{{m}^{2}})}{0.1256{{m}^{2}}}=165.39N$

Es decir, que necesitamos 165.39 Newtons de fuerza , para poder levantar el bloque de 50,000 Newtons de peso.

Ejercicios de Presión para Practicar

Para mejorar el aprendizaje del tema de Presión es importante que el alumno intente resolver los siguientes ejercicios y posteriormente compruebe sus resultados con la solución paso a paso que hemos realizado. 😀

Ver Solución

Ver Solución

Ver Solución

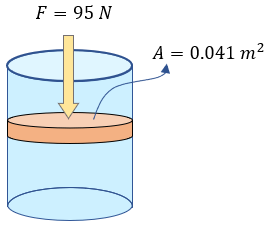
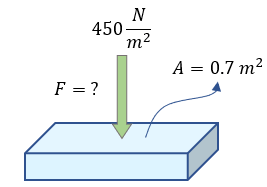
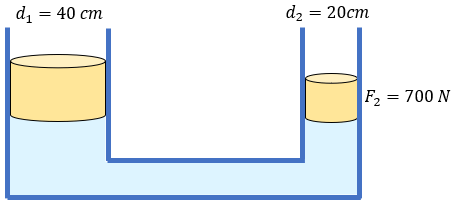
Examen de Presión Hidrostática

Ahora es momento de evaluar tus conocimientos teóricos sobre la materia, ¿estás listo?