Potencia Mecánica - Ejercicios Resueltos

Otro de los temas importantes en la dinámica es el concepto físico de la potencia mecánica que se puede definir como la rapidez con la que se realiza un trabajo. Y sus unidades en el sistema internacional se miden en watts (W), en honor al escocés James Watt (1736 – 1819), el Watt significa un trabajo de Joule realizado en un segundo.

pero ¿de dónde proviene el concepto de potencia mecánica? Sabemos que el ser humano siempre ha buscado de alguna forma realizar su trabajo en el menor tiempo posible, de ahí la necesidad de introducir a la rapidez para poder efectuarlo, por eso decimos que la potencia mecánica es la rapidez con que se ejecuta un trabajo.

📏 Fórmula de la Potencia Mecánica

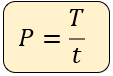
Dónde:

P = potencia en J/s = Watts (W)

T = trabajo realizado en Joules (J)

t = tiempo en que se realiza el trabajo en segundos (s)

Otra forma de expresar a la potencia es mediante la siguiente fórmula:

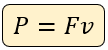
Dónde:

P = potencia en J/s = Watts (W)

F = Fuerza (N)

v = velocidad (m/s)

En esta expresión podemos conocer la potencia si conocemos la magnitud de la velocidad que adquiere un cuerpo u objeto, misma que tendrá una dirección y sentido igual a la de la fuerza que recibe.

📄 Ejercicios Resueltos de Potencia Mecánica

Ahora es momento de realizar algunos ejemplos o ejercicios de Potencia Mecánica

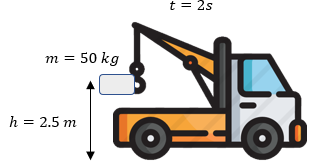
Solución:

Vamos anotar nuestros datos para la solución de este ejercicio, recordemos que se habla no de un solo bulto de cemento, sino de 60.

🔔 Datos:

m = 50 kg * 60 = 3000 kg

h = 2.5 m

t = 2s

P = ?

Con los datos obtenidos podemos pensar en la siguiente fórmula de potencia:

$\displaystyle P=\frac{T}{t}$

Aunque el trabajo sabemos que es el producto de la fuerza por distancia, entonces tenemos:

$\displaystyle P=\frac{T}{t}=\frac{{Fd}}{t}$

Recordar que la masa obtenida por los bultos de cemento son masa pero no fuerza (o sea peso), entonces:

$\displaystyle P=\frac{T}{t}=\frac{{Fd}}{t}=\frac{{mgd}}{t}=\frac{{\left( {3000kg} \right)(9.8\frac{m}{{{{s}^{2}}}})(2.5m)}}{{2s}}=36750W$

El resultado de la potencia mecánica efectuada por la grúa es de:

36 750 Watts

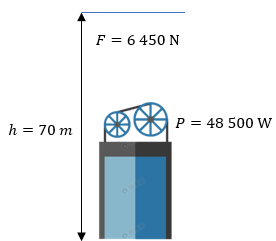
Solución:

Colocando nuestros datos:

🔔 Datos:

P = 48 500 W

h = 70 m

F (peso) = 6 450 N

t = ?

Aplicando nuestra fórmula:

$\displaystyle P=\frac{T}{t}$

involucrando a la fuerza y distancia (que es Trabajo):

$\displaystyle P=\frac{{Fd}}{t}$

Despejando al "tiempo"

$\displaystyle t=\frac{{Fd}}{P}$

Ahora sustituimos nuestros datos en la fórmula:

$\displaystyle t=\frac{{Fd}}{P}=\frac{{\left( {6450N} \right)\left( {70m} \right)}}{{48500N}}=9.3s$

Por lo que obtenemos un tiempo de:

9.3 segundos

Solución: 

En este ejercicio observamos que se utiliza el término "hp" que significa "caballo de fuerza", y en física esta unidad se puede convertir con los Watts. El factor de conversión es el siguiente:

$\displaystyle 1hp=746W$

Teniendo en cuenta esto, coloquemos los datos:

🔔 Datos:

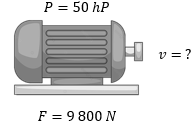
P = 50 hp

F = 9 800 N

v = ?

Realizando la conversión de unidades:

$\displaystyle 50hp\left( {\frac{{746W}}{{1hp}}} \right)=37300W$

Ahora la fórmula que ocuparemos será la siguiente:

$\displaystyle v=\frac{P}{F}$

sustituyendo estos datos en nuestra fórmula, obtenemos:

$\displaystyle v=\frac{P}{F}=\frac{{37300W}}{{9800N}}=3.806\approx 3.81\frac{m}{s}$

Es decir que la velocidad para elevar la carga es de:

3.81 m/s