Regla de Cramer + Ejercicios Resueltos

En Fisimat sabemos que la Regla de Cramer es una de las aplicaciones más importantes e interesantes que existen dentro del álgebra lineal, y que puede ser de mucha ayuda para resolver sistema de ecuaciones lineales, problemas donde necesitemos encontrar el valor de las incógnitas, sin embargo como todo proceso matemático que requiere cálculo es importante tener que cumplir ciertas reglas, para no fallar en la solución de éste teorema.

Contenidos

¿Quién fue Gabriel Cramer?
¿Cuándo utilizar la regla de Cramer?
1. Cuando no utilizar la regla de Cramer
¿En qué consiste la regla de Cramer?
1. Para un sistema 2x2
2. Para un sistema 3x3
Ejercicio Resueltos de la Regla de Cramer 2x2
Ejercicios Resueltos de la Regla de Cramer 3x3
Ejercicios para practicar

¿Quién fue Gabriel Cramer?

No nos extenderemos mucho sobre la vida de Gabriel Cramer, puesto que existen diversas biografías de el en internet, sin embargo algo que debemos de tener en cuenta es que Gabriel Cramer, es reconocido como uno de los grandes matemáticos del siglo XVII, de origen Suizo, y que trabajó en grandes obras de diferentes matemáticos tales como Jean Bernoulli, Jacques Bernoulli, y los estudios sobre determinantes que había investigado Leibniz.

Cramer adoptó gran parte el trabajo de Cardan de 1545, donde dicho matemático había dado ciertos algoritmos obre como resolver un sistema de ecuaciones lineales de 2x2 , a esto Cardan le llamó "Regla de Modo", que corresponde en esencia a lo que hoy conocemos como Regla de Cramer.

¿Cuándo utilizar la regla de Cramer?

No siempre podemos utilizar la regle de cramer, debemos de tener en cuenta un punto muy importante y quizá único para poder cumplir con los requisitos de la Regla de Cramer, es importante considerar que el número de ecuaciones sea igual al número de incógnitas.

Es decir, si vamos a utilizar un sistema de 2x2, entonces solo habrán 2 incógnitas, y si es de 3x3 por ende sería un sistema con 3 incógnitas ¿difícil de entender?, no.. Para nada, es la única regla que debemos seguir para utilizar este método.

Cuando no utilizar la regla de Cramer

A pesar de decir claramente cuando utilizar la regla de Cramer, también podríamos generalizar en dos puntos, donde no debemos aplicar la regla de Cramer, o al menos no es tan conveniente hacerlo.

Solamente es aplicable cuando el determinante de la matriz es diferente de cero, es decir cuando el sistema tiene una única solución en caso contrario es imposible resolverlo.
El segundo inconveniente proviene de la dificultad de resolver un sistema mucho más grande que 3x3, se vuelve más complejo tedioso resolver por regla de cramer sistemas de nxn con n muy grande. Así que pensar dos veces antes de resolver matrices de 4x4, 5x5, etc..

¿En qué consiste la regla de Cramer?

Este método permite emplear a los determinantes para la resolución de sistema de ecuaciones, veamos el siguiente el siguiente análisis.

Para un sistema 2x2

Sea el sistema de 2x2 :

$\displaystyle \begin{array}{l}{{a}_{1}}x+{{a}_{2}}y={{a}_{3}}\\{{b}_{1}}x+{{b}_{2}}y={{b}_{3}}\end{array}$

Podemos definir 3 cosas muy importantes del sistema de ecuaciones.

Determinante del sistema:

$\displaystyle \Delta s=\left| \begin{matrix} {{a}_{1}} & {{a}_{2}} \\ {{b}_{1}} & {{b}_{2}} \\ \end{matrix} \right|$

Determinante de "x" :

$\displaystyle \Delta x=\left| \begin{matrix} {{a}_{3}} & {{a}_{2}} \\ {{b}_{3}} & {{b}_{2}} \\ \end{matrix} \right|$

Determinante de "y"

$\displaystyle \Delta y=\left| \begin{matrix} {{a}_{1}} & {{a}_{3}} \\ {{b}_{1}} & {{b}_{3}} \\ \end{matrix} \right|$

Por la regla de Cramer entonces podemos decir que para encontrar los valores de "x" y "y" tendríamos que aplicar lo siguiente:

Para "x"

$\displaystyle x=\frac{\Delta x}{\Delta s}=\frac{\left| \begin{matrix} {{a}_{3}} & {{a}_{2}} \\ {{b}_{3}} & {{b}_{2}} \\ \end{matrix} \right|}{\left| \begin{matrix} {{a}_{1}} & {{a}_{2}} \\ {{b}_{1}} & {{b}_{2}} \\ \end{matrix} \right|}$

Para "y"

$\displaystyle y=\frac{\Delta y}{\Delta s}=\frac{\left| \begin{matrix} {{a}_{1}} & {{a}_{3}} \\ {{b}_{1}} & {{b}_{3}} \\ \end{matrix} \right|}{\left| \begin{matrix} {{a}_{1}} & {{a}_{2}} \\ {{b}_{1}} & {{b}_{2}} \\ \end{matrix} \right|}$

Teniendo en cuenta esta definición, podemos resolver problemas de 2x2 sin dificultad alguna.

Para un sistema 3x3

Se dice que es un sistema de 3x3, si posee tres ecuaciones con tres incógnitas, cada una de las ecuaciones que forman parte de un sistema de 3x3 se le interpreta también como un plano en el espacio tridimensional. Pero de esto hablaremos en otro tema. Por ahora nos interesa conocer que un sistema de 3x3 está formado con la siguiente estructura:

$\displaystyle \left\{ \begin{matrix} ax+by+cz=m \\ dx+ey+fz=n \\ gx+hy+iz=r \\ \end{matrix} \right.$

Podemos estructurar las diversas formas de determinante para encontrar los valores de "x" de "y" y de "z", así que procedemos a colocarlos en el arreglo correspondiente.

Para obtener a "x", aplicaremos:

$\displaystyle x=\frac{\Delta x}{\Delta s}=\frac{\left| \begin{matrix} m & b & c \\ n & e & f \\ r & h & i \\ \end{matrix} \right|}{\left| \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right|}$

Para obtener a "y", aplicaremos:

$\displaystyle y=\frac{\Delta y}{\Delta s}=\frac{\left| \begin{matrix} a & m & c \\ d & n & f \\ g & r & i \\ \end{matrix} \right|}{\left| \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right|}$

Para obtener a "z", aplicaremos:

$\displaystyle z=\frac{\Delta z}{\Delta s}=\frac{\left| \begin{matrix} a & b & m \\ d & e & n \\ g & h & r \\ \end{matrix} \right|}{\left| \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right|}$

Con esto podemos resolver, cualquier sistema de ecuaciones de 3x3, pasar a la zona de ejemplos resueltos de éste tipo. 😀

Ejercicio Resueltos de la Regla de Cramer 2x2

Ejemplo 1: Resuelva mediante la Regla de Cramer el siguiente sistema de ecuaciones lineales:

$\displaystyle \begin{array}{l}-3x+4y=5\\x-9y=-2\end{array}$

Ordenaremos conforme la regla de Cramer deduce, así que:

$\displaystyle x=\frac{\Delta x}{\Delta s}=\frac{\left| \begin{matrix} 5 & 4 \\ -2 & -9 \\ \end{matrix} \right|}{\left| \begin{matrix} -3 & 4 \\ 1 & -9 \\ \end{matrix} \right|}=\frac{(-45)-(-8)}{(-3)(-9)-(4)(1)}=-\frac{37}{23}$

Por lo tanto, el valor de "x" es -37/23

Ahora procedemos a calcular el valor de "y"

$\displaystyle y=\frac{\Delta y}{\Delta s}=\frac{\left| \begin{matrix} -3 & 5 \\ 1 & -2 \\ \end{matrix} \right|}{\left| \begin{matrix} -3 & 4 \\ 1 & -9 \\ \end{matrix} \right|}=\frac{6-5}{(-3)(-9)-(4)(1)}=\frac{1}{23}$

Por lo tanto, el valor de "y" es 1/23

Luego, la solución del sistema es

$\displaystyle \left( -\frac{37}{23},\frac{1}{23} \right)$

En Fisimat, somos de la idea de que un ejemplo no es suficiente, resolvamos el siguiente ejercicio.

Ejemplo 2: Resuelva el siguiente sistema de ecuaciones 2x2 mediante la regla de Cramer:

$\displaystyle \begin{array}{l}x-5y=8\\-7x+8y=25\end{array}$

Ordenando conforme marca la Regla de Cramer, tanto para "x" como para "y", y tenemos:

$\displaystyle x=\frac{\Delta x}{\Delta s}=\frac{\left| \begin{matrix} 8 & -5 \\ 25 & 8 \\ \end{matrix} \right|}{\left| \begin{matrix} 1 & -5 \\ -7 & 8 \\ \end{matrix} \right|}=\frac{64-(-5)(25)}{(1)(8)-(-5)(-7)}=-\frac{189}{27}=-7$

Por lo tanto, el valor de "x" es 7

Ahora procedemos a calcular el valor de "y"

$\displaystyle y=\frac{\Delta y}{\Delta s}=\frac{\left| \begin{matrix} 1 & 8 \\ -7 & 25 \\ \end{matrix} \right|}{\left| \begin{matrix} 1 & -5 \\ -7 & 8 \\ \end{matrix} \right|}=\frac{25-(-7)(8)}{(1)(8)-(-5)(-7)}=-\frac{81}{27}=-3$

Por lo tanto, el valor de "y" es 3

Luego, la solución del sistema es:

$\displaystyle \left( -7,3 \right)$

¡¡Muy fácil!! ¿cierto?

Ejercicios Resueltos de la Regla de Cramer 3x3

Llegó el momento de resolver ejercicios paso a paso mediante la regla de Cramer, es importante que hasta este punto ya puedas resolver determinantes de 3x3 mediante la regla de Sarrus, en caso de no tener esta habilidad, necesitarás repasar este artículo en el siguiente link https://www.fisimat.com.mx/determinantes/, para no tener dificultades al momento de realizar los siguientes ejemplos:

Ejemplo 3 Resuelve mediante la regla de Cramer, el siguiente sistema de ecuaciones

$\displaystyle \left\{ \begin{matrix} 3x-y+z=7 \\ -2x+y-z=-5 \\ 4x+7y+5z=1 \\ \end{matrix} \right.$

Solución:

Antes de empezar a resolver este ejercicio, recordemos un poco la regla de Sarrus para el sistema de 3x3.

Si nuestro sistema de 3x3 fuera de la siguiente forma:

$\displaystyle \left| \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right|$

Entonces la solución por Sarrus, sería:

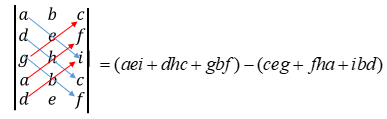
Las líneas azules indican la forma en la que se irán multiplicando, y vemos como obtenemos un triple producto por cada una de ellas, y las líneas rojas hacen exactamente lo mismo, solo que éstas se restarán de las azules, tal como la imagen de arriba.

Teniendo en cuenta esto, y esperando te hayas acordado de la regla de Sarrus, podemos comenzar a resolver el sistema de 3x3.

La solución para "x", es:

$\displaystyle x=\frac{\Delta x}{\Delta s}=\frac{\left| \begin{matrix} 7 & -1 & 1 \\ -5 & 1 & -1 \\ 1 & 7 & 5 \\ \end{matrix} \right|}{\left| \begin{matrix} 3 & -1 & 1 \\ -2 & 1 & -1 \\ 4 & 7 & 5 \\ \end{matrix} \right|}=\frac{24}{12}=2$

La solución para "y", es:

$\displaystyle y=\frac{\Delta y}{\Delta s}=\frac{\left| \begin{matrix} 3 & 7 & 1 \\ -2 & -5 & -1 \\ 4 & 1 & 5 \\ \end{matrix} \right|}{\left| \begin{matrix} 3 & -1 & 1 \\ -2 & 1 & -1 \\ 4 & 7 & 5 \\ \end{matrix} \right|}=-\frac{12}{12}=-1$

La solución para "z", es:

$\displaystyle z=\frac{\Delta z}{\Delta s}=\frac{\left| \begin{matrix} 3 & -1 & 7 \\ -2 & 1 & -5 \\ 4 & 7 & 1 \\ \end{matrix} \right|}{\left| \begin{matrix} 3 & -1 & 1 \\ -2 & 1 & -1 \\ 4 & 7 & 5 \\ \end{matrix} \right|}=\frac{0}{12}=0$

Por lo que la solución del sistema de ecuaciones lineales con tres variables, es la siguiente terna ordenada:

$\displaystyle \left( 2,-1,0 \right)$

Ejemplo 4 Resuelve el siguiente problema mediante la regla de Cramer

$\displaystyle \left\{ \begin{matrix} -x+2y+4z=1 \\ 4x+6y-2z=2 \\ x-y+6z=3 \\ \end{matrix} \right.$

Recuerda aplicar de la mejor manera el método de Sarrus, para no tener ningún problema con los valores.

La solución para "x" es:

$\displaystyle x=\frac{\Delta x}{\Delta s}=\frac{\left| \begin{matrix} 1 & 2 & 4 \\ 2 & 6 & -2 \\ 3 & -1 & 6 \\ \end{matrix} \right|}{\left| \begin{matrix} -1 & 2 & 4 \\ 4 & 6 & -2 \\ 1 & -1 & 6 \\ \end{matrix} \right|}=\frac{-82}{-126}=\frac{41}{63}$

La solución para "y" es:

$\displaystyle y=\frac{\Delta y}{\Delta s}=\frac{\left| \begin{matrix} -1 & 1 & 4 \\ 4 & 2 & -2 \\ 1 & 3 & 6 \\ \end{matrix} \right|}{\left| \begin{matrix} -1 & 2 & 4 \\ 4 & 6 & -2 \\ 1 & -1 & 6 \\ \end{matrix} \right|}=\frac{-4}{-126}=\frac{2}{63}$

La solución para "z" es:

$\displaystyle z=\frac{\Delta z}{\Delta s}=\frac{\left| \begin{matrix} -1 & 2 & 1 \\ 4 & 6 & 2 \\ 1 & -1 & 3 \\ \end{matrix} \right|}{\left| \begin{matrix} -1 & 2 & 4 \\ 4 & 6 & -2 \\ 1 & -1 & 6 \\ \end{matrix} \right|}=\frac{-50}{-126}=\frac{25}{63}$

Por lo que la solución de la siguiente terna es:

$\displaystyle \left( \frac{41}{63},\frac{2}{63},\frac{25}{63} \right)$

Ejercicios para practicar

Ahora es momento de la práctica con los ejercicios propuestos y repasar todo lo aprendido y mejorar tus habilidades, así que veamos:

$\displaystyle \left\{ \begin{matrix} x-2y=7 \\ 3x-y=6 \\ \end{matrix} \right.$

$\displaystyle \left\{ \begin{matrix} x-5y=8 \\ -7x+8y=25 \\ \end{matrix} \right.$

$\displaystyle \left\{ \begin{matrix} 3x-2y=13 \\ 2x+4y=3 \\ \end{matrix} \right.$

$\displaystyle \left\{ \begin{matrix} x+y+z=6 \\ x-y+2z=5 \\ x-y-3z=-10 \\ \end{matrix} \right.$

$\displaystyle \left\{ \begin{matrix} 6x+3y+2z=12 \\ 9x-y+4z=37 \\ 10x+5y+3z=21 \\ \end{matrix} \right.$

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

21 Comentarios Publicados

Ana Victoria Michel dice:

5 mayo, 2019 a las 10:46 pm

Muchas gracias, me sirvió mucho.

Responder
1. Carlos julián dice:
  
  6 mayo, 2019 a las 9:08 am
  
  Nos da mucho gusto Ana! Saludos.
  
  Responder
  1. stevenpacho dice:
    
    30 enero, 2020 a las 11:57 am
    
    gracias
    
    Responder
  2. Ivonne dice:
    
    7 marzo, 2020 a las 9:59 pm
    
    4r - 4s + 4r = -4
    4r + s - 2t =5
    -3r - 3s - 4t= -16
    Como se hace ese
    
    Responder
LEIDY dice:

6 noviembre, 2019 a las 9:46 pm

MUCHAS GRACIAS, ME SIRVIO DEMASIADO!!

Responder
Kiran Ahmed dice:

11 noviembre, 2019 a las 9:31 am

muchas gracias, pude entender y corregir mis errores

Responder
Ivonne dice:

7 marzo, 2020 a las 9:59 pm

4r - 4s + 4r = -4
4r + s - 2t =5
-3r - 3s - 4t= -16
Como se hace ese

Responder
ANGEL MANUEL dice:

18 marzo, 2020 a las 4:09 pm

Su ayuda con este problema , no me sale
Calcula la determinante del siguiente arreglo.
4 −4 6
5 2 7
5 −5 1 -

Responder
ANGEL MANUEL dice:

18 marzo, 2020 a las 4:10 pm

No entiendo de matrices helppp
En una tienda se venden 3 tipos de cosméticos diferentes, los cuales son labiales, sombras e iluminadores, en total en un día se venden 100 piezas en los siguientes precios 20, 25 y 30 respectivamente, con un ingreso total de 2375 pesos. Como dato adicional se notifica que se vendieron 2 sombras menos que los labiales

Responder
karla martinez dice:

8 abril, 2020 a las 10:58 am

Necesito 5 ejercicios con su explicación paso por paso plis!

Responder
Clarence dice:

11 junio, 2020 a las 7:31 pm

Y que pasaría si en donde si en vez de la Z solo hay números, ejemplo: 3x-y+6=5

Responder
1. Gëövänny dice:
  
  19 julio, 2022 a las 8:52 pm
  
  Me sirvió mucho gracias
  
  Responder
Karla dice:

17 diciembre, 2020 a las 4:14 pm

Le pude entender perfectamente a los ejercicios, fueron de mucha ayuda, gracias.

Responder
Karla dice:

17 diciembre, 2020 a las 4:18 pm

Le pude entender perfectamente a los ejercicios, fue de mucha ayuda, gracias.

Responder
1. Carlos julián dice:
  
  22 marzo, 2021 a las 11:04 am
  
  Gracias a ti Karla!
  
  Responder
Lorena dice:

27 abril, 2021 a las 4:50 pm

Muchísimas gracias me ayudaron mucho

Responder
Rafael dice:

22 junio, 2021 a las 12:00 pm

He recordado con su ayuda el método, Gracias

Responder
Gëövänny dice:

19 julio, 2022 a las 8:51 pm

Me sirvió muchas gracias

Responder
[email protected] dice:

28 agosto, 2023 a las 1:19 pm

podria checar los determinantes

Responder
[email protected] dice:

28 agosto, 2023 a las 1:20 pm

podria checar los determinantes de los ejercicios

Responder
[email protected] dice:

28 agosto, 2023 a las 1:41 pm

excelente

Responder

Deja una respuesta Cancelar la respuesta