Determinantes + Ejercicios Resueltos

¿Qué tal amig@s? , el día de hoy hablaremos sobre las determinantes y las diversas aplicaciones que podemos utilizar con esta gran herramienta del álgebra lineal, desde calcular el área y volumen de ciertas figuras. Así que antes de entrar a resolver ejercicios, debemos comprender la teoría, aunque no sea tan profunda, pero debemos comprender de donde proviene y las reglas que debemos de seguir antes de volvernos unos cracks en la práctica 😎

Bien, las determinantes están vinculadas con las matrices cuadradas , es decir; aquellas matrices que tienen el mismo número de filas que de columnas, en este artículo solo estaremos resolviendo determinantes de tamaño 2x2 y 3x3, pero más grandes no, ¿por qué?, pues bien. El hecho de tener una determinante de 4x4 , 5x5 o más, implica un trabajo muy laborioso, y se tiene que recurrir ya sea a calculadoras gratificadoras, o software como Matlab, Wolfram, etc..

Contenidos

¿Que son las determinantes?
1. ¿Cómo se calcula una determinante de 2x2?
2. ¿Cómo se calcula una determinante de 3x3?
Ejercicios Resueltos de Determinantes de 2x2
Ejercicios Resueltos de Determinantes de 3x3
Ejercicios Propuestos

¿Que son las determinantes?

A pesar de que para profundizar sobre el tema de las determinantes necesitamos leer los estudios que hicieron los grandes matemáticos de siglos atrás, las determinantes todavía siguen teniendo un valor muy importante dentro de las ramas de las matemáticas y sus diversas aplicaciones.

Un determinante es un número asociado a una matriz cuadrada, es un solo número que posee valor, dicho número es obtenido por diversos productos realizados con los elementos de la matriz.

¿Cómo se calcula una determinante de 2x2?

Imaginemos que tenemos la siguiente matriz de orden 2, cada elemento de la matriz tendrá una variable, para que se entienda mucho mejor el proceso.

$\displaystyle A=\left( \begin{matrix} a & b \\ c & d \\ \end{matrix} \right)$

Bien, ahora procedemos a calcular la determinante de A.

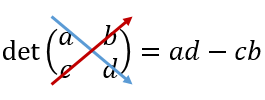
Si observamos, el proceso de multiplicación fue demasiado fácil.

La flecha azul indica: Qué se multiplica el primer elemento de la matriz (a) con el cuarto elemento (d), esto da como resultado = a*d

La flecha roja indica: Qué se multiplica el tercer elemento de la matriz (c) con el segundo elemento (b), esto da como resultado = c*b

Cuando se procede a multiplicar (linea azul), siempre debe comenzar el signo negativo, y después multiplicar (linea roja). ¿se entiende?

Pero ¿qué pasaría si se tratara de una matriz de 3x3?

¿Cómo se calcula una determinante de 3x3?

Cuando tenemos una matriz cuadrada 3x3, y deseamos calcular la determinante, forzosamente debemos recurrir a una regla práctica, conocida como Regla de Sarrus , ¿pero cómo la aplicamos?, bien, primero debemos pensar en nuestra matriz de 3x3.

$\displaystyle A=\left( \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{matrix} \right)$

1️⃣ Vamos a tomar las primeras dos columnas de la matriz A, y las vamos a colocar de lado derecho, de la siguiente forma:

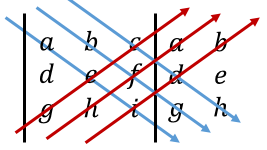
2️⃣ Multiplicamos los tres números que están alineados en cada flecha, conservando el signo que poseen en cada producto, tome en cuenta que cuando se regresa la operación en la flecha roja, debe ir un signo negativo.

Quedando así los productos:

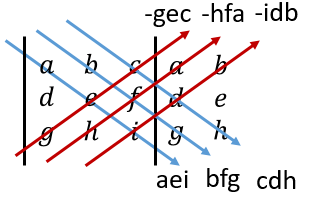
Esto quiere decir que sin duda nuestra determinante de 3x3, la podemos escribir de la siguiente forma:

$\displaystyle \det (A)=(aei+bfg+cdh)-(gec+hfa+idb)$

Hemos factorizado el signo negativo, para hacer el proceso más limpio y menos confuso. 😎

Bien, pero no hay nada más entendible, que con ejercicios resueltos paso a paso, así que vamos a ello 😀

Pierre F. Sarrus

Sarrus fue un matemático Francés, que nació el 10 de marzo de 1798, conocido por haber introducido la regla para el cálculo de determinantes de 3×3 en una de sus artículos llamado «Nouvelles méthodes pour la résolution des équations».

Ejercicios Resueltos de Determinantes de 2x2

Veamos un ejemplo para hacerlo más sencillo.

Ejemplo 1: Resuelva la siguiente determinante de la siguiente Matriz A

Solución:

Sea la Matriz A:

$\displaystyle A=\left( \begin{matrix} 3 & 9 \\ -4 & 7 \\ \end{matrix} \right)$

Si recordamos el proceso para calcular una determinante de 2x2, entonces sabremos que debemos multiplicar el (3) con el (7) , posteriormente colocar el signo negativo, y proceder al siguiente producto (-4) con (9), de ahí realizar la operación aritmética, de la siguiente forma:

$\displaystyle \det (A)=(3)(7)-(9)(-4)=21+36=57$

Por lo tanto, la determimante de la matriz A es 57.

Veamos otro ejemplo.

Ejemplo 2: Calcule la siguiente determinante de la Matriz B

Solución:

Sea la matriz B:

$\displaystyle B=\left( \begin{matrix} -2 & -5 \\ 3 & 8 \\ \end{matrix} \right)$

Realizamos el mismo algoritmo que en el ejemplo 1, para proceder al cálculo.

$\displaystyle \det (B)=(-2)(8)-(3)(-5)=-16+15=-1$

Veamos un último ejemplo para una determinante de 2x2

Ejemplo 3: Calcule la siguiente determinante de la Matriz C

Solución:

Sea la matriz C:

$\displaystyle C=\left( \begin{matrix} -3 & 2 \\ -1 & 5 \\ \end{matrix} \right)$

Como hemos explicado, realizamos el procedimiento anterior y aplicamos las multiplicaciones.

$\displaystyle \det (C)=(-3)(5)-(-1)(2)=-15+2=-13$

Muy, pero muy fácil.

Ahora veamos como resolver determinantes de 3x3.

Ejercicios Resueltos de Determinantes de 3x3

Ejemplo 4: Resuelva la siguiente determinante de la siguiente Matriz D

Solución:

Sea la matriz D:

$\displaystyle D=\left| \begin{matrix} 1 & 0 & -2 \\ 3 & 2 & -1 \\ 4 & -3 & 0 \\ \end{matrix} \right|$

Vamos a extender las primeras dos columnas, a lado derecho. Tal como se explico en la definición de cálculo de determinantes de 3x3. Una vez logrando esta parte, tendremos lo siguiente:

$\displaystyle \left| \begin{matrix} 1 & 0 & -2 \\ 3 & 2 & -1 \\ 4 & -3 & 0 \\ \end{matrix} \right|\begin{matrix} 1 & 0 \\ 3 & 2 \\ 4 & -3 \\ \end{matrix}$

Imaginando la posición de las flechas, las primeras que van hacía abajo ,nos daría los siguientes productos:

$\displaystyle \left| \begin{matrix} 1 & 0 & -2 \\ 3 & 2 & -1 \\ 4 & -3 & 0 \\ \end{matrix} \right|\begin{matrix} 1 & 0 \\ 3 & 2 \\ 4 & -3 \\ \end{matrix}=\left\{ \begin{matrix} (1)(2)(0)+ \\ (0)(-1)(4)+ \\ (-2)(3)(-3) \\ \end{matrix}=0+0+18 \right.$

Ahora, calculando el producto de las flechas que van hacía arriba, tendríamos:

$\displaystyle \left| \begin{matrix} 1 & 0 & -2 \\ 3 & 2 & -1 \\ 4 & -3 & 0 \\ \end{matrix} \right|\begin{matrix} 1 & 0 \\ 3 & 2 \\ 4 & -3 \\ \end{matrix}=\left\{ \begin{matrix} (4)(2)(-2)+ \\ (-3)(-1)(1)+ \\ (0)(3)(0) \\ \end{matrix} \right.=-16+3+0=-13$

Por lo que el determinante final, nos daría:

$\displaystyle \det (D)=18-(-13)=18+13=31$

Así que la Det(D) = 31

Veamos otro ejemplo:

Ejemplo 5: Resuelva la siguiente determinante de la siguiente Matriz E

Solución:

Sea la matriz E:

$\displaystyle E=\left| \begin{matrix} 2 & -1 & 0 \\ 1 & 3 & -1 \\ 2 & 0 & -2 \\ \end{matrix} \right|$

Nuevamente extendemos las dos columnas principales a lado derecho:

$\displaystyle \left| \begin{matrix} 2 & -1 & 0 \\ 1 & 3 & -1 \\ 2 & 0 & -2 \\ \end{matrix} \right|\begin{matrix} 2 & -1 \\ 1 & 3 \\ 2 & 0 \\ \end{matrix}$

Realizamos los productos hacía abajo.

$\displaystyle \left| \begin{matrix} 2 & -1 & 0 \\ 1 & 3 & -1 \\ 2 & 0 & -2 \\ \end{matrix} \right|\begin{matrix} 2 & -1 \\ 1 & 3 \\ 2 & 0 \\ \end{matrix}=\left\{ \begin{matrix} (2)(3)(-2)+ \\ (-1)(-1)(2)+ \\ (0)(1)(0) \\ \end{matrix}=-12+2+0=-10 \right.$

Ahora procedemos aplicar los productos pero hacía arriba.

$\displaystyle \left| \begin{matrix} 2 & -1 & 0 \\ 1 & 3 & -1 \\ 2 & 0 & -2 \\ \end{matrix} \right|\begin{matrix} 2 & -1 \\ 1 & 3 \\ 2 & 0 \\ \end{matrix}=\left\{ \begin{matrix} (2)(3)(0)+ \\ (0)(-1)(2)+ \\ (-2)(1)(-1) \\ \end{matrix}=0+0+2=2 \right.$

Ahora si podemos realizar el paso final para la determinante.

$\displaystyle \det (E)=-10-(2)=-10-2=-12$

Por lo que el cálculo de la det(E) = 12

😀

¿fácil no?

Ejercicios Propuestos

Es momento de practicar, 💡recuerda realizar las operaciones cuidadosamente para evitar problemas con los signos.

Calcule las siguiente determinantes:

$\displaystyle D=\left| \begin{matrix} -3 & 1 \\ -1 & 5 \\ \end{matrix} \right|$

$\displaystyle B=\left| \begin{matrix} 1 & -9 \\ -3 & 2 \\ \end{matrix} \right|$

$\displaystyle F=\left| \begin{matrix} 1 & 1 & -1 \\ 0 & 1 & 2 \\ 2 & 1 & -1 \\ \end{matrix} \right|$

$\displaystyle R=\left| \begin{matrix} 6 & 1 & 0 \\ 2 & 2 & -2 \\ 0 & 1 & 1 \\ \end{matrix} \right|$

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

1 Comentarios Publicados

Miguel Jordan Verano dice:

23 mayo, 2023 a las 6:35 pm

Favor como resolver este determinante:
t-2 4 3
1 t+1 -2
0 0 t-4

Responder

Deja una respuesta Cancelar la respuesta