Solución Problema 1 del Principio de Bernoulli

Con este primer problema del Principio de Bernoulli el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula del principio de Bernoulli, recuerde que es importante que conozca las ecuaciones de Gasto y Continuidad, para comprender mucho mejor el tema puede resolver el ejercicios cuentas veces desee 😊👇

Nivel de Dificultad: ⭐⭐⭐⭐

Problema 3.- Del punto A al punto B de la tubería fluye agua a 10°C a razón de 0.37 m³/s si la presión en A es de 66.2kPa, calcule la presión en B.

Problema del principio de Bernoulli

Solución:

Antes de poder darle solución completa al problema, es importante primero que deduzcamos la fórmula que aplicaremos, ya que algunas cosas pueden simplificarse o no, tal como hemos hecho en los problemas anteriores. Por ahora el problema nos pide la presión en el punto B. Recordemos entonces la fórmula del principio de Bernoulli

$\displaystyle \frac{{{v}_{1}}^{2}}{2}+g{{h}_{1}}+\frac{{{p}_{1}}}{{{\rho }_{1}}}=\frac{{{v}_{2}}^{2}}{2}+g{{h}_{2}}+\frac{{{p}_{2}}}{{{\rho }_{2}}}$

Como estamos hablando en términos de A y B, podemos quitar a 1 y 2 y poner la ecuación en términos de A y B.

$\displaystyle \frac{{{v}_{A}}^{2}}{2}+g{{h}_{A}}+\frac{{{p}_{A}}}{{{\rho }_{A}}}=\frac{{{v}_{B}}^{2}}{2}+g{{h}_{B}}+\frac{{{p}_{B}}}{{{\rho }_{B}}}$

Despejando a la presión en B "Pb"

$\displaystyle \frac{{{p}_{B}}}{{{\rho }_{B}}}=\frac{{{v}_{A}}^{2}}{2}+g{{h}_{A}}+\frac{{{p}_{A}}}{{{\rho }_{A}}}-\frac{{{v}_{B}}^{2}}{2}-g{{h}_{B}}$

$\displaystyle {{p}_{B}}=\frac{{{\rho }_{B}}{{v}_{A}}^{2}}{2}+g{{h}_{A}}{{\rho }_{B}}+\frac{{{\rho }_{B}}{{p}_{A}}}{{{\rho }_{A}}}-\frac{{{\rho }_{B}}{{v}_{B}}^{2}}{2}-g{{h}_{B}}{{\rho }_{B}}$

Recordemos que tanto la densidad en A como la densidad en B es la misma, porque se trata del agua. Entonces la podemos simplificar:

$\displaystyle {{p}_{B}}=\frac{{{\rho }_{B}}{{v}_{A}}^{2}}{2}+g{{h}_{A}}{{\rho }_{B}}+{{p}_{A}}-\frac{{{\rho }_{B}}{{v}_{B}}^{2}}{2}-g{{h}_{B}}{{\rho }_{B}}$

Ordenando nuestra fórmula:

$\displaystyle {{p}_{B}}={{p}_{A}}+\frac{{{\rho }_{B}}{{v}_{A}}^{2}}{2}-\frac{{{\rho }_{B}}{{v}_{B}}^{2}}{2}+g{{h}_{A}}{{\rho }_{B}}-g{{h}_{B}}{{\rho }_{B}}$

Factorizando nuestra fórmula:

$\displaystyle {{p}_{B}}={{p}_{A}}+\frac{{{\rho }_{B}}}{2}\left( {{v}_{A}}^{2}-{{v}_{B}}^{2} \right)+g{{\rho }_{B}}\left( {{h}_{A}}-{{h}_{B}} \right)$

$\displaystyle {{p}_{B}}={{p}_{A}}+{{\rho }_{B}}\left[ \left( \frac{{{v}_{A}}^{2}-{{v}_{B}}^{2}}{2} \right)+g\left( {{h}_{A}}-{{h}_{B}} \right) \right]$

Ahora si, podemos decir que ya hemos obtenido la fórmula que aplicaremos para la solución del ejercicio.

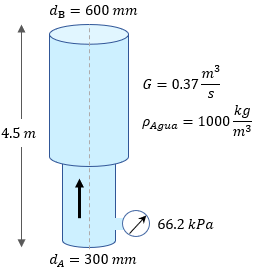
Datos del problema:

$\displaystyle {{h}_{A}}=0m$

$\displaystyle {{h}_{B}}=4.5m$

$\displaystyle {{d}_{A}}=300mm\left( \frac{1m}{1000mm} \right)=0.3m$

$\displaystyle {{d}_{B}}=600mm\left( \frac{1m}{1000mm} \right)=0.6m$

$\displaystyle {{p}_{A}}=66.2kPa$

$\displaystyle G=0.37\frac{{{m}^{3}}}{s}$

$\displaystyle {{\rho }_{agua}}=1000\frac{kg}{{{m}^{3}}}$

a) Encontrando la presión en el punto B

Si analizamos bien el ejercicio, nos daremos cuenta que no contamos con la velocidad en A ni la velocidad en B, por lo tanto es importante poder calcularlos. Y esto más fácil aún cuando contamos con el dato del Gasto.

$\displaystyle {{G}_{A}}={{A}_{A}}{{v}_{A}}$

Despejando a la velocidad en A y calculando.

$\displaystyle {{v}_{A}}=\frac{{{G}_{A}}}{{{A}_{A}}}=\frac{0.37\frac{kg}{{{m}^{3}}}}{\frac{\pi {{\left( 0.3m \right)}^{2}}}{4}}=5.23\frac{m}{s}$

Para calcular la velocidad en B, aplicamos el principio de la ecuación de continuidad:

$\displaystyle {{A}_{A}}{{v}_{A}}={{A}_{B}}{{v}_{B}}$

Qué también la podemos escribir de esta forma:

$\displaystyle {{G}_{A}}={{A}_{B}}{{v}_{B}}$

Si despejamos a la velocidad en V, entonces obtendremos lo siguiente:

$\displaystyle {{v}_{B}}=\frac{{{G}_{A}}}{{{A}_{B}}}=\frac{0.37\frac{kg}{{{m}^{3}}}}{\frac{\pi {{\left( 0.6m \right)}^{2}}}{4}}=1.31\frac{m}{s}$

Excelente... Ahora que ya tenemos ambas velocidades, podemos hacer uso de la fórmula y resolver la presión en B

$\displaystyle {{p}_{B}}={{p}_{A}}+{{\rho }_{B}}\left[ \left( \frac{{{v}_{A}}^{2}-{{v}_{B}}^{2}}{2} \right)+g\left( {{h}_{A}}-{{h}_{B}} \right) \right]$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{p}_{B}}=66.2kPa+1000\frac{kg}{{{m}^{3}}}\left[ \left( \frac{{{5.23}^{2}}-{{1.31}^{2}}}{2} \right)+9.81\frac{m}{{{s}^{2}}}\left( 0-4.5 \right) \right]$

$\displaystyle {{p}_{B}}=66.2kPa+1000\frac{kg}{{{m}^{3}}}\left[ 12.82+9.81\frac{m}{{{s}^{2}}}\left( -4.5 \right) \right]$

$\displaystyle {{p}_{B}}=66.2kPa+1000\frac{kg}{{{m}^{3}}}\left( 12.82-44.145 \right)$

$\displaystyle {{p}_{B}}=66.2kPa+1000\frac{kg}{{{m}^{3}}}\left( -31.325 \right)$

$\displaystyle {{p}_{B}}=66.2kPa-31325Pa=34875Pa=34.87kPa$

Es decir que nuestra presión en el punto B es de 34,875 Pascales = 34.87 kPa

Resultado:

$\displaystyle {{p}_{B}}=34.87kPa$

4 Comentarios Publicados

Rocío dice:

4 mayo, 2023 a las 10:08 am

Holaaa! Tengo dudas de donde salen los 34875??

Responder
1. Esteban dice:
  
  11 julio, 2023 a las 8:01 pm
  
  El ejercicio está mal escrito, porque no puedes con trabajar con kPa y Pa a la vez. Hay que hacer la conversión de kPa a Pa para resolverlo y ahi te dará el resultado.
  
  Responder
Matteo dice:

31 octubre, 2023 a las 11:13 am

Hola!, Tengo una inquietud, a mi me dio al final de todo 34920, pero el resultado es de 34875. Me podrian explicar por favor?

Responder
vittorio dice:

21 febrero, 2024 a las 12:33 pm

esta mal escritas las velocidades, v1 es igual 0,524m/s
y v2 es gual a a 0,130 m/s

Responder

Deja una respuesta Cancelar la respuesta