Programa para resolver integrales y derivadas en linea

Uno de los problemas más cotidianos que nos podemos encontrar a la hora de estar cursando una asignatura o materia de cálculo diferencial o integral, es que al momento de resolver algún problema o ejercicio necesitamos estar seguro si nuestro resultado es correcto o incorrecto, y muchas veces buscamos la manera de encontrar esa herramienta que nos permita hacerlo.

Esta vez te traigo un de los programas en linea más sofisticados y potentes para llevar a cabo esa tarea, y no solo eso, sino que tiene un sin fin de herramientas que podemos usar para poder resolver otro tipo de problemas, en este caso nos enfocaremos solamente en las derivadas e integrales.

Lo primero que tenemos que hacer, es entrar en la página oficial de WolframAlpha  una vez estando dentro, tendremos una pantalla similar a esta:

Ahí, en esa pantalla, tenemos que colocar nuestro código para poder resolver tanto las integrales como las derivadas. ¿Código? Ha dicho ¿Código?, no te asustes, no se trata de un tipo de programación tedioso y aburrido, ahora lo que vamos hacer es plantearnos una integral sencilla de tal modo que sepamos nosotros que el programa está haciendo bien su papel de ayudarnos a resolver una integral, probemos con la siguiente integral:

sabemos cual es resultado de esa integral algebraica, por lo que ahora vamos colocar lo siguiente en el cuadro de WolframAlpha:

Esto, nos generará lo siguiente en el cuadro de Wolfram:

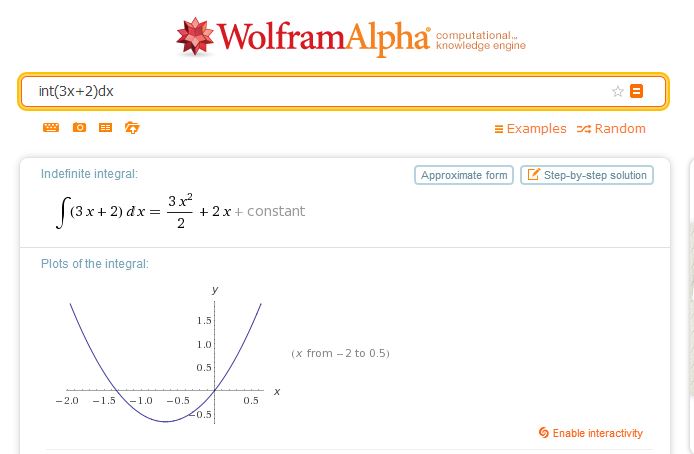
Puuuuf!! :O  Genial ¿no?.  No solo te genera la integral sino que también te da una gráfica de la función que estás integrando, esto para darte la idea de lo que estás realizando, pero aún hay más.

Si das click en la parte que dice Step-by-step solution podrás encontrar el método paso a paso para poder llegar al resultado, y eso está muy interesante, porque nos permitirá ver una infinidad de soluciones.

En el caso de las derivadas es similar, solo tienes que variar el código que se colocó al inicio, por ejemplo:

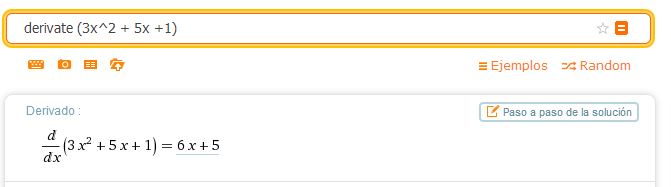
derivate (3x^2 + 5x +1) , esto nos dará la derivada de dicha función dentro, si lo realizamos nos daremos cuenta que:

observemos que dice Wolfram al respecto.

De lo mejor con Wolfram ¿no?,  Espero que les haya gustado este pequeño tutorial de como usar esta gran herramienta en linea, y de sacarle el máximo provecho para esas tediosas derivadas e integrales 🙂