Campo Magnético producido por un conductor recto
Para comprender al campo magnético producido por un conductor recto, es necesario decir de la importancia de la ley de Biot-Savart para calcular la intensidad del campo magnético alrededor de conductores con los más variados formatos. En el caso particular de conductores rectos y largos, como los cables que utilizamos rutinariamente; la corriente eléctrica de intensidad I genera un campo magnético cuyas líneas de fuerza son circunferencias concéntricas, situadas en planos perpendiculares al alambre. En cada circunferencia, se determina la intensidad del vector de inducción magnética B por la Ley de Ampere.
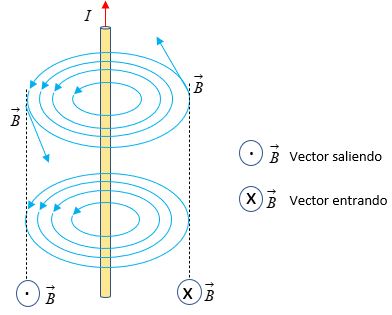
En la imagen se ilustra perfectamente lo que se quiere dar a entender.
📄 Fórmula del Campo Magnético Producido por un Conductor Recto
Para entender mucho mejor este tema, es importante analizar la fórmula del campo magnético que es producida por el conductor recto.
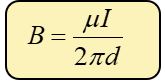
Dónde:
I = Intensidad de corriente que circula por el conductor (A)
μ = Permeabilidad del medio que rodea al conductor, se expresa en Tm/A
B = Inducción magnética o densidad de flujo magnético en un punto determinado perpendicular al conductor, se mide en teslas. (T)
d = distancia perpendicular entre el conductor y el punto considerado, se mide en metros (m).
📙 Ejercicios Resueltos de Campo Magnético Producido por un Conductor Recto
Como siempre decimos en Fisimat, no podemos detallar más la teoría de un tema, sino realizamos ejercicios para poder practicar sobre este tema.
Problema 1. Calcular la inducción magnética o densidad de flujo en el aire, en un punto a 10 cm de un conductor recto por el que circula una intensidad de corriente de 2.5 A.
Solución:
Analicemos todos los datos que tenemos:
B = ?
I = 2.5 A
d = 10 cm = 0.1 m
$\displaystyle {{\mu }_{0}}=4\pi x{{10}^{{-7}}}\frac{{Tm}}{A}$
Ahora solo nos queda sustituir nuestros datos en la fórmula, recordar que la distancia la hemos convertido a metros, es por eso que los 10 cm son equivalentes a 0.1 metros.
$\displaystyle B=\frac{{{{\mu }_{0}}I}}{{2\pi d}}$
Sustituyendo:
$\displaystyle B=\frac{{{{\mu }_{0}}I}}{{2\pi d}}=\frac{{\left( {4\pi x{{{10}}^{{-7}}}\frac{{Tm}}{A}} \right)\left( {2.5A} \right)}}{{2\pi \left( {0.1} \right)}}=5x{{10}^{{-6}}}T$
Obtenemos un valor de 5x10^-6 Teslas
-
Prof. Elio Verde, Liceo de Aplicación, Caracas. dice:
De cómo se puede calcular el valor del campo magnético terrestre en la zona en donde se hace el experimento.
1. Se coloca un alambre recto y libre en un circuito eléctrico de fuente, resistencia, amperímetro e interruptor.
2.- Se coloca una aguja montada no imantada ferromagnética sobre un pivote, semejante a una guía de brújula. de tal manera que el conductor y la aguja estén en la dirección de las lineas de campo magnético terrestre, formando, valga la iteración, de 0 grados.
3.- Encienda el circuito y mida la corriente eléctrica que puede ser de 1 o 2 amperios, no importa otra cantidad menor o mayor.
4.- Verá que la aguja se moverá de acuerdo al campo magnético generado según la Ley de Ampere a distintas distancias.
5.- Colóquelo a una distancia por debajo del campo creado tal que forme un ángulo de 45º. Calcule el campo magn según la Ley de Ampere y ese será el valor del campo magnético terrestre.
2 Comentarios Publicados
Deja una respuesta
Temas que podrían interesarte 👇