Campo Magnético producido por una Bobina

Para poder hablar de un campo magnético que es generado por una bobina es importante primero definir. ¿Qué es una bobina? La bobina es el producto de enrollar un alambre (espira) sobre un eje de tal manera que tenga un número N de vueltas y en consecuencia pueda generar un campo magnético cuando por esta circule una corriente I

La bobina es consecuencia de las espiras, es por ello por lo que la fórmula que se utiliza para calcular su campo magnético no es indiferente de la primera, solamente se agregará un valor o factor más, que son los números de vueltas.

🧲 Fórmula del campo magnético generado por una bobina

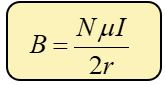
Hay que recordar que el campo magnético producido es generado en su centro, no en cualquier punto. Solo en el centro.

Dónde:

I = Intensidad de corriente que circula por la bobina (A)

μ = Permeabilidad del medio en el centro de la bobina, se expresa en Tm/A

B = Inducción magnética en el centro de la bobina, se mide en teslas. (T)

r = radio de la espira, se mide en metros (m)

N = Número de vueltas o cantidad de espiras sobre un cierto eje

📙 Ejercicios Resueltos de Campo Magnético Producido por una Bobina

No se puede entender un problema a ciencia cierta sino tenemos ejercicios resueltos del tema, así que para comprender un poco más veamos algunos ejemplos.

🔴 Solución:

Lo primero que haremos para poder calcular el radio de dicha bobina, es tener en cuenta que en nuestra fórmula debemos realizar un despeje, sino recuerdas como despejar, puedes empezar por aquí. 👇

¿Cómo despejar fórmulas?

De la fórmula:

$\displaystyle B=\frac{{N\mu I}}{{2r}}$

Despejando, nos quedaría:

$\displaystyle r=\frac{{N\mu I}}{{2B}}$

Ahora si, esta sería la fórmula a utilizar, entonces debemos anotar nuestros datos.

Datos:

N = 600 espiras (vueltas de alambre)

I = 9 A

B = 8 x 10 ^ (-3) T

$\displaystyle \mu ={{\mu }_{0}}=4\pi x{{10}^{{-7}}}\frac{{Tm}}{A}$

▶ Sustitución

Vamos a sustituir nuestros datos en la fórmula de "r" que previamente despejamos:

$\displaystyle r=\frac{{N\mu I}}{{2B}}=\frac{{(600)(4\pi x{{{10}}^{{-7}}})(9A)}}{{2(8x{{{10}}^{{-3}}}T)}}=0.135m$

Obtenemos un radio de 0.135 metros, que convertidos en centímetros, son:

$\displaystyle r=0.135m\left( {\frac{{100cm}}{{1m}}} \right)=13.5cm$

Lo que equivale a 13.5 centímetros de radio.