Límites Trigonométricos - Ejercicios Resueltos

En el cálculo diferencial nos encontramos con un tema importante para comprender muy bien a las funciones y se trata de los límites trigonométricos.

Un límite trigonométrico es una expresión matemática que se utiliza para determinar el valor de una función trigonométrica en un punto en el que la función puede no estar definida. Los límites trigonométricos se utilizan en cálculo y otras áreas de las matemáticas para investigar el comportamiento de las funciones trigonométricas en puntos específicos o en el límite de un intervalo dado. Dentro de los límites de este tipo podemos observar la siguiente identidad que nos ayudará a resolver muchos ejemplos:

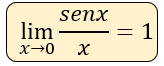
Utilizando este límite, se puede obtener la serie de otros límites trigonométricos:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\tan x}}{x}=1$

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\operatorname{arcs}enx}}{x}=1$

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\arctan x}}{x}=1$

Además, suponemos que los ángulos se miden en radianes.

Ejemplos Resueltos de Límites Trigonométricos

Para entender mucho mejor el tema, comencemos a resolver algunos ejercicios.

Solución:

Se puede observar que no es un límite complicado, sin embargo hay que aplicar las propiedades pertinentes y resolver:

Vamos a multiplicar la función principal por 3 y dividirla por 3:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{4x}}{{\sin 3x}}=\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{3\cdot 4x}}{{3\sin 3x}}$

Posteriormente sacamos el factor 4/3 y el límite nos quedará así:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{4x}}{{\sin 3x}}=\frac{4}{3}\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{3x}}{{\sin 3x}}$

Dividiendo la función por 3x , obtenemos:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{4x}}{{\sin 3x}}=\frac{4}{3}\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{1}{{\frac{{\sin 3x}}{{3x}}}}$

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{4x}}{{\sin 3x}}=\frac{4}{3}\frac{{\underset{{x\to 0}}{\mathop{{\lim }}}\,1}}{{\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin 3x}}{{3x}}}}$

Puesto que $\displaystyle 3x\to 0$ como $\displaystyle x\to 0$ , podemos escribir:

$\displaystyle \frac{4}{3}\frac{{\underset{{x\to 0}}{\mathop{{\lim }}}\,1}}{{\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin 3x}}{{3x}}}}=\frac{4}{{3\underset{{3x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin 3x}}{{3x}}}}=\frac{4}{{3\cdot 1}}=\frac{4}{3}$

Que sería el resultado de nuestro límite trigonométrico

Solución:

Lo primero que haremos será factorizar el numerador, pues se trata de una identidad trigonométrica:

$\displaystyle \cos 3x-\cos x=-2\sin \frac{{3x-x}}{2}\sin \frac{{3x+x}}{2}$

Simplificando la igualdad:

$\displaystyle \cos 3x-\cos x=-2\sin x\sin 2x$

Esto produce que nuestro límite ahora se exprese de la siguiente manera:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\cos 3x-\cos x}}{{{{x}^{2}}}}=\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\left( {-2senxsen2x} \right)}}{{{{x}^{2}}}}$

Aplicando un poco de álgebra, y por propiedades de límites, obtenemos:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\cos 3x-\cos x}}{{{{x}^{2}}}}=-2\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{senx}}{x}\cdot \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{sen2x}}{x}$

Justo aquí encontramos el primer límite notable $\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{senx}}{x}=1$

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\cos 3x-\cos x}}{{{{x}^{2}}}}=-2\left( 1 \right)\cdot 2\underset{{2x\to 0}}{\mathop{{\lim }}}\,\frac{{sen2x}}{{2x}}$

Y finalmente, esto nos daría:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\cos 3x-\cos x}}{{{{x}^{2}}}}=-2\left( 1 \right)\cdot 2(2)=-4$

Por lo tanto la respuesta es -4

Solución:

Aplicando la siguiente identidad trigonométrica:

$\displaystyle senx-seny=2sen\frac{{x-y}}{2}\cos \frac{{x+y}}{2}$

Entonces nuestro límite se transforma de la siguiente manera:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{sen5x-sen3x}}{{senx}}=\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{2sen\frac{{5x-3x}}{2}\cos \frac{{5x+3x}}{2}}}{{senx}}$

Reduciendo el límite:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{2sen\frac{{2x}}{2}\cos \frac{{8x}}{2}}}{{senx}}=\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{2senx\cos 4x}}{{senx}}$

Simplifando senx/senx

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{2senx\cos 4x}}{{senx}}=\underset{{x\to 0}}{\mathop{{\lim }}}\,2\cos 4x$

Por lo tanto obtenemos:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\left( {2\cos 4x} \right)=2\underset{{x\to 0}}{\mathop{{\lim }}}\,\cos 4x=2\cdot \cos \left( {4\cdot 0} \right)=2\cdot 1=2$

Y tenemos como resultado 2

Solución:

Para darle solución a este límite trigonométrico, utilizamos la siguiente identidad trigonométrica:

$\displaystyle \cos \alpha -\cos \beta =-2sen\frac{{\alpha +\beta }}{2}sen\frac{{\alpha -\beta }}{2}$

Esto va generar que nuestra función del numerador tome la siguiente forma:

$\displaystyle \cos (x+\alpha )-\cos (x-\alpha )=-2sen\frac{{x+\alpha +x-\alpha }}{2}sen\frac{{x+\alpha -\left( {x-\alpha } \right)}}{2}$

Reduciendo los términos, obtenemos:

$\displaystyle \cos (x+\alpha )-\cos (x-\alpha )=-2sen\frac{{2x}}{2}sen\frac{{2\alpha }}{2}$

Simplificando aún más:

$\displaystyle \cos (x+\alpha )-\cos (x-\alpha )=-2senxsen\alpha $

Ahora, si podemos reescribir el límite principal, quedando entonces:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\cos \left( {x+a} \right)-\cos \left( {x-a} \right)}}{x}=\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{-2senxsen\alpha }}{x}$

Ahora si, obtenemos el resultado de nuestro límite:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{-2senxsen\alpha }}{x}=-2\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{senx}}{x}sen\alpha =-2sen\alpha $

Solución:

Aplicaremos una movimiento algebraico para poder resolver este ejercicio:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin ax}}{{\sin bx}}=\underset{{x\to 0}}{\mathop{{\lim }}}\,\left( {\frac{{\sin ax}}{{\sin bx}}\cdot \frac{a}{b}\cdot \frac{{bx}}{{ax}}} \right)$

Posterirmente a eso, aplicaremos lo siguiente:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin ax}}{{\sin bx}}=\underset{{x\to 0}}{\mathop{{\lim }}}\,\left( {\frac{{\sin ax}}{{ax}}\cdot \frac{{bx}}{{\sin bx}}\cdot \frac{a}{b}} \right)$

Después aplicamos:

$\displaystyle \underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin ax}}{{\sin bx}}=\frac{a}{b}\frac{{\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin ax}}{{ax}}}}{{\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin bx}}{{bx}}}}$

Obviamente $\displaystyle ax\to 0$ y $\displaystyle bx\to 0$ como $\displaystyle x\to 0$ . Entonces:

$\displaystyle L=\frac{a}{b}\frac{{\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin ax}}{{ax}}}}{{\underset{{x\to 0}}{\mathop{{\lim }}}\,\frac{{\sin bx}}{{bx}}}}=\frac{a}{b}\cdot \frac{1}{1}=\frac{a}{b}$

Por lo tanto la respuesta es:

a/b