Máximos y Mínimos de una Función

Si ya aprendimos a derivar funciones, ahora es momento de ver las diversas aplicaciones que podemos utilizar, y los máximos y mínimos de una función son sin duda un ejemplo claro para que veamos la importancia del cálculo diferencial.

¿Qué es un Máximo y qué es un Mínimo?

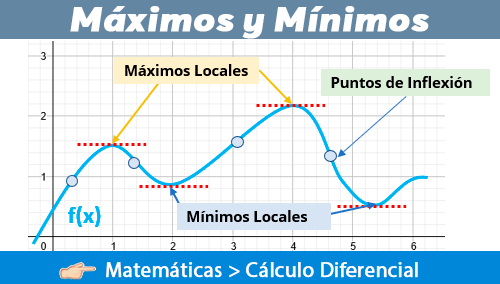
Para entender que es un máximo y que es un mínimo, y las diversas interpretaciones que podemos encontrar en los libros de cálculo diferencial e integral, veamos la siguiente imagen.

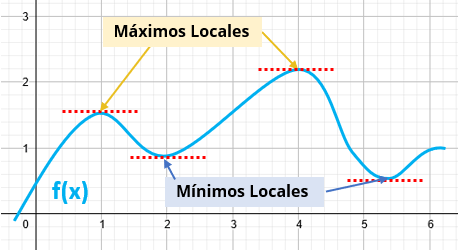
Un Máximo Local es un punto de la función donde ésta cambia de creciente a decreciente, es decir, aquellos puntos altos de la gráfica.

Un Mínimo Local es un punto de la función donde ésta cambia de decreciente a creciente, es decir, aquellos puntos bajos de la gráfica.

Pasos para calcular el máximo y mínimo de una función

Para poder calcular el máximo y mínimo de una función tenemos que seguir los siguientes pasos.

1. Se deriva la función y = f(x) y esta se iguala a cero.
2. Se buscan las raíces de la ecuación resultante , dichos valores se llaman valores críticos y son los que hacen que la tangente tenga pendiente cero  (horizontal), pueda darnos un máximo o un mínimo.
3. Para saber si se trata de un máximo o mínimo, se toma un valor un poco menor al crítico y este se sustituye en la derivada, y se hace lo mismo para un valor mayor al crítico. Como resultado veremos lo siguiente; si el valor de la derivada cambia de positivo a negativo, el valor crítico en análisis es de un máximo, si cambia de negativo a positivo, se trata de un mínimo, y si no cambia en ningún sentido, entonces se trata de un punto de inflexión.

Para entender mucho mejor este concepto, veamos el siguiente ejemplo.

Máximos y Mínimos - Ejercicios Resueltos

Solución:

Por cuestiones académicas vamos a graficar la función, solamente para que observes el resultado y lo que vamos a obtener aplicando los máximos y mínimos de la función.

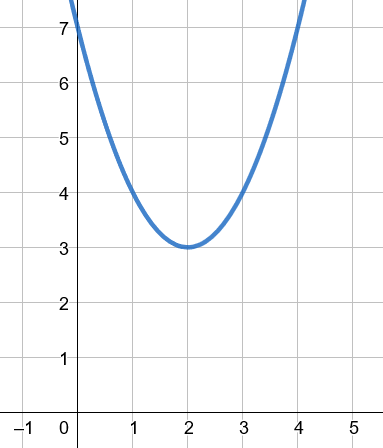
Si analizamos la gráfica, vemos que solamente existe un mínimo, no hay máximos. ¿Pero como se hace con las derivadas? ¿cómo encuentro ese punto?, bien, vamos a ello 😀

 Paso 1:  Vamos a derivar la función e igualamos a cero, es decir.

$latex \displaystyle \frac{d}{dx}\left( {{x}^{2}}-4x+7 \right)=0$

Como resultado

$latex \displaystyle 2x-4=0$

 Paso 2: Vamos a despejar a "x" , y el valor que nos de es al que llamaremos valor crítico 

$latex \displaystyle 2x=4$

$latex \displaystyle x=\frac{4}{2}=2$

Entonces podemos decir que:

x = 2

Sabemos que hay un máximo o un mínimo pero no sabemos donde, (aunque por la gráfica de arriba si sabemos donde está). Pero analíticamente aún lo desconocemos. 

 Paso 3:  Vamos asignar un valor menor al valor crítico y lo vamos a sustituir en la derivada:

> Eligiendo a x = 1 Porque es un valor menor al valor crítico.

$latex \displaystyle \frac{dy}{dx}=2x-4=2(1)-4=2-4=-2$

Ok! Ahora haremos lo mismo, pero asignando un valor mayor.

> Eligiendo a x = 3 porque es un valor mayor al valor crítico.

$latex \displaystyle \frac{dy}{dx}=2x-4=2(3)-4=6-4=+2$

Comprobación: 

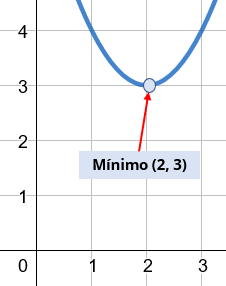
Para comprobar, como ya sabemos que existe un mínimo en x = 2 , entonces vamos a sustituir a x = 2 en la función original, la que derivamos. De esta forma:

$latex \displaystyle y={{x}^{2}}-4x+7={{(2)}^{2}}-4(2)+7=4-8+7=3$

y = 3

Esto quiere decir que nuestro mínimo se encuentra en las coordenadas m(2,3) , si vemos la gráfica eso es cierto 😀

Solución:

Muchas veces los máximos y mínimos funcionan como herramientas para graficar una función de forma rápida, pero en este blog para términos académicos colocamos primero las gráficas, y después analizamos de forma analítica, con la intención de que el alumno aprenda los conceptos de forma entendible.

Entonces, graficamos la función:

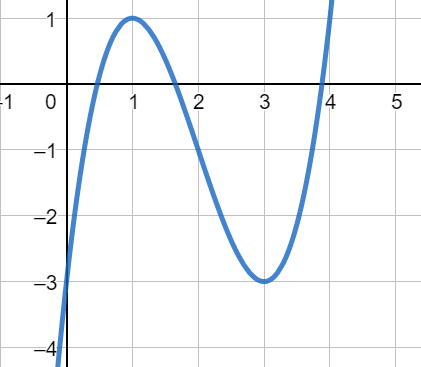
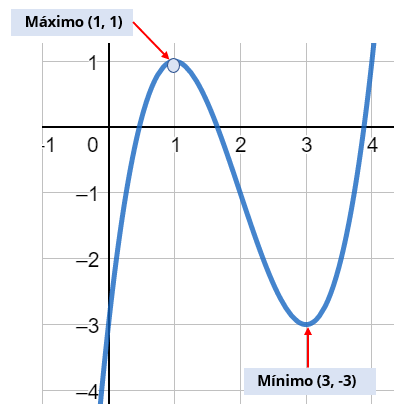
Es lógico saber que nuestra función tiene tanto un máximo como un mínimo e incluso podemos apreciar las coordenadas. Pero nuevamente, ¿cómo las obtenemos de forma analítica?

 Paso 1:  Derivamos la función e igualamos a cero:

$latex \displaystyle \frac{d}{dx}({{x}^{3}}-6{{x}^{2}}+9x-3)=0$

Como resultado de la derivada:

$latex \displaystyle 3{{x}^{2}}-12x+9=0$

 Paso 2:  Vamos a obtener los valores críticos porque la ecuación que nos dio de la derivada es una función cuadrática, procedemos de manera algebraica a encontrar esos valores.

Si dividimos nuestra ecuación sobre 3, esto nos daría:

$latex \displaystyle \frac{3{{x}^{2}}-12x+9}{3}=\frac{0}{3}$

$latex \displaystyle {{x}^{2}}-4x+3=0$

Esto es más fácil de factorizar.

$latex \displaystyle (x-1)(x-3)=0$

Por lo tanto: x = 1 y x = 3 son valores críticos.

 Paso 3:  Vamos asignar un valor menor al valor crítico y lo vamos a sustituir en la derivada.

Analizando el primer valor crítico x = 1

Valor menor --> x = 0

$latex \displaystyle 3{{x}^{2}}-12x+9=3{{(0)}^{2}}-12(0)+9=+9$

Valor mayor --> x = 2

$latex \displaystyle 3{{x}^{2}}-12x+9=3{{(2)}^{2}}-12(2)+9=12-24+9=-3$

Analizando el primer valor crítico x = 3

Valor menor: --> x = 2

Como ya sabemos el resultado para x = 2, porque lo hicimos en el paso anterior, colocamos el resultado:

$latex \displaystyle 3{{x}^{2}}-12x+9=3{{(2)}^{2}}-12(2)+9=12-24+9=-3$

Valor mayor --> x = 4

$latex \displaystyle 3{{x}^{2}}-12x+9=3{{(4)}^{2}}-12(4)+9=48-48+9=9$

Comprobación: 

Para comprobar, como ya sabemos que existe un máximo en x = 1 , y un mínimo en x = 3, entonces vamos a sustituir a x = 1 y x = 3 en la función original. De esta forma:

Comprobando con x = 1

$latex \displaystyle y={{x}^{3}}-6{{x}^{2}}+9x-3={{(1)}^{3}}-6{{(1)}^{2}}+9(1)-3=1$

y = 1

Esto quiere decir que existe un máximo en las coordenadas m (1,1).

Comprobando con x = 3

$latex \displaystyle y={{x}^{3}}-6{{x}^{2}}+9x-3={{(3)}^{3}}-6{{(3)}^{2}}+9(3)-3=27-54+27-3=-3$

y = 3

Esto quiere decir que existe un mínimo en las coordenadas m (3, -3)

Veamos ahora un ejemplo real de aplicación en Física.

Dónde

h = altura

t = tiempo

Solución: 

Sabemos por el problema que la altura máxima lo alcanzará cuando la derivada de la función se iguale a cero, entonces derivamos e igualamos.

$latex \displaystyle h=3+14t-5{{t}^{2}}$

Derivando

$latex \displaystyle \frac{dh}{dt}=14-10t$

Igualando a cero

$latex \displaystyle 14-10t=0$

Despejamos a "t".

$latex \displaystyle 14=10t$

$latex \displaystyle t=\frac{14}{10}=1.4$

Esto quiere decir que cuando t = 1.4 segundos se alcanza la altura máxima. ¿Cómo sabemos a qué altura?, solamente tenemos que sustituir nuestro valor del tiempo en la función original. Tal como lo hicimos en los ejercicios anteriores.

$latex \displaystyle h=3+14t-5{{t}^{2}}=3+14(1.4)-5{{(1.4)}^{2}}=12.8$

Graficando el problema

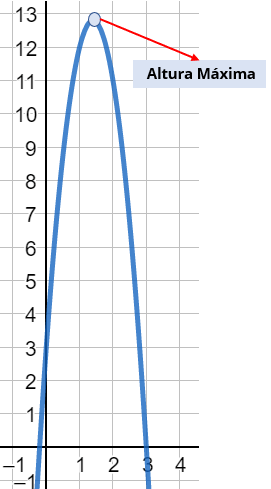
Esto quiere decir que la altura máxima es de 12.8 metros a los 1.4 segundos 😀