¿Qué es la entropía?

La entropía (termino procedente del griego, y que significa “vuelta” o “transformación”)  es un concepto crucial tanto para la física como para la química , así como para otras ciencias tales como la informática, las matemáticas y la lingüística.

Enfocándonos en el campo de la termodinámica, se entiende por entropía (simbolizada como S) a una magnitud física que para un sistema termodinámico en equilibrio mide el número de microestados compatibles con el macroestado de equilibrio, también se puede decir que mide el grado de organización del sistema, o que es la razón de un incremento entre energía interna frente a un incremento de temperatura del sistema.

La entropía, en esencia, es una medida que calcula la probabilidad de que ocurran cambios en el sistema en función de la probabilidad de sus microestados.

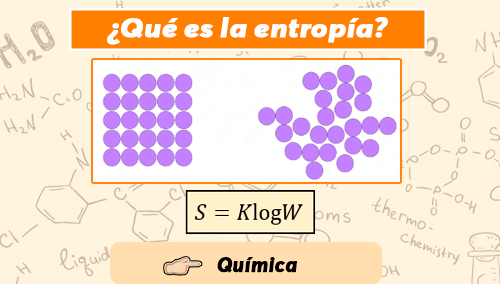
La función termodinámica de entropía es central para el segundo principio de la termodinámica. La entropía puede interpretarse como una medida de la distribución aleatoria de un sistema. Se dice que un sistema altamente distribuido al azar tiene alta entropía. Un sistema en una condición improbable tendrá una tendencia natural a reorganizarse a una condición más probable (similar a una distribución al azar), reorganización que dará como resultado un aumento de la entropía. La entropía alcanzará un máximo cuando el sistema se acerque al equilibrio, y entonces se alcanzará la configuración de mayor probabilidad. Por lo tanto, se entiende por entropía a la medida del desorden de un sistema, y en este sentido, está asociada a un grado de homogeneidad.

La entropía es una función de estado de carácter extensivo y su valor, en un sistema aislado, crece en el transcurso de un proceso que se da de forma natural. La entropía describe lo irreversible de los sistemas termodinámicos.

La variación de entropía nos muestra la variación del orden molecular ocurrido en una reacción química. La entropía de formación de un compuesto químico se establece midiendo la que conforma a cada uno de sus elementos constituyentes. A mayor entropía de formación, más favorable será su formación. Por lo tanto, si el incremento de entropía es positivo, los productos presentan un mayor desorden molecular (mayor entropía) que los reactivos. En cambio, cuando el incremento es negativo, los productos son más ordenados.

La entropía puede ser la magnitud física termodinámica que permite medir la parte no utilizable de la energía contenida en un determinado sistema. Esto quiere decir que dicha parte de la energía no puede usarse para producir un trabajo o esfuerzo. De esta forma, la entropía podría ser descrita como la energía que resulta desechable ante un proceso termodinámico, aquella energía que no es utilizada y que por tanto no es considerada útil para tal proceso.

¿Cómo calcular la entropía?

La entropía se puede definir como la medida cuantitativa del desorden o aleatoriedad en un sistema. El concepto proviene de la termodinámica , que se ocupa de la transferencia de energía térmica dentro de un sistema. En lugar de hablar sobre alguna forma de "entropía absoluta", los físicos suelen generalmente hablar sobre el cambio de entropía que tiene lugar en un proceso termodinámico específico.

Cálculo de entropía

En un proceso isotérmico , el cambio en la entropía (delta-S) es el cambio en el calor ( Q ) dividido por la temperatura absoluta ( T ):

$\displaystyle \Delta S=\frac{Q}{T}$

En cualquier proceso termodinámico reversible, se puede representar en cálculo como la integral de un estado inicial de un proceso a su estado final de dQ / T .

$\displaystyle S=\int{\frac{dQ}{T}}$

En un sentido más general, la entropía es una medida de la probabilidad y el desorden molecular de un sistema macroscópico. En un sistema que puede describirse por variables, hay una cierta cantidad de configuraciones que pueden asumir esas variables. Si cada configuración es igualmente probable, entonces la entropía es el logaritmo natural del número de configuraciones, multiplicado por la constante de Boltzmann.

$\displaystyle S={{k}_{B}}\ln W$

donde S es entropía, Kb es la constante de Boltzmann, ln es el logaritmo natural y W representa el número de estados posibles. La constante de Boltzmann es igual a:

$\displaystyle {{K}_{B}}=1.38065x{{10}^{-23}}\frac{J}{K}$

Unidades de entropía

La entropía se considera una propiedad extensa de la materia que se expresa en términos de energía dividida por la temperatura. Las unidades en el sistema internacional (SI), suelen colocarse como J / K (joules / grados Kelvin).

Entropía y la segunda ley de la termodinámica

Una forma de establecer la segunda ley de la termodinámica es:

En cualquier sistema cerrado, la entropía del sistema permanecerá constante o aumentará.

Una forma de ver esto es que agregar calor a un sistema hace que las moléculas y los átomos se aceleren. Puede ser posible (aunque complicado) revertir el proceso en un sistema cerrado (es decir, sin extraer energía o liberar energía en otro lugar) para alcanzar el estado inicial, pero nunca se puede obtener todo el sistema "menos enérgico" de lo que comenzó, la energía simplemente no tiene ningún lugar adonde ir. Para procesos irreversibles, la entropía combinada del sistema y su entorno siempre aumenta.

Conceptos erróneos sobre la entropía

Esta visión de la segunda ley de la termodinámica es muy popular y ha sido mal utilizada. Algunos sostienen que la segunda ley de la termodinámica significa que un sistema nunca puede volverse más ordenado. No es verdad. Simplemente significa que para volverse más ordenado (para que la entropía disminuya), debe transferir energía desde algún lugar fuera del sistema, como cuando una mujer embarazada extrae energía de los alimentos para hacer que el óvulo fertilizado se convierta en un bebé completo, completamente en alinearse con las disposiciones de la segunda línea.

También conocido como: Desorden, Caos, Aleatoriedad (los tres sinónimos imprecisos)

Entropía absoluta

Un término relacionado es "entropía absoluta", que se denota por S en lugar de Δ S . La entropía absoluta se define según la tercera ley de la termodinámica. Aquí se aplica una constante que lo hace para que la entropía en el cero absoluto se defina como cero.

Fórmula para el cálculo de la Entropía

1. Para procesos con calor específico constante:

$\displaystyle \Delta S = m \cdot c \cdot \ln\left( \frac{T_f}{T_i} \right)$

Donde:

• $\displaystyle m$ es la masa del cuerpo (en kilogramos, kg)

• $\displaystyle c$ es el calor específico del material (en J/kg·K)

• $\displaystyle T_i$ es la temperatura inicial (en kelvin, K)

• $\displaystyle T_f$ es la temperatura final (en kelvin, K)

Esta fórmula se usa cuando un sólido o líquido se calienta o enfría de forma reversible sin cambio de fase y con un calor específico constante.

2. Para gases ideales en procesos isotérmicos (a temperatura constante):

$\displaystyle \Delta S = n \cdot R \cdot \ln\left( \frac{V_f}{V_i} \right)$

Donde:

• $\displaystyle n$ es el número de moles de gas

• $\displaystyle R = 8.314\ \text{J/mol·K}$ es la constante universal de los gases

• $\displaystyle V_i$ y $\displaystyle V_f$ son los volúmenes inicial y final del gas (en litros o metros cúbicos, pero deben tener las mismas unidades)

Esta fórmula se aplica cuando un gas ideal se expande o comprime isotérmicamente (es decir, manteniendo la temperatura constante) en un proceso reversible.

3. Para gases ideales a presión constante:

$\displaystyle \Delta S = n \cdot C_p \cdot \ln\left( \frac{T_f}{T_i} \right)$

Donde:

• $\displaystyle C_p$ es el calor molar a presión constante, que depende del tipo de gas:

  • Monoatómico: $\displaystyle C_p = \frac{5}{2}R$

  • Diatómico: $\displaystyle C_p = \frac{7}{2}R$

Esta ecuación se usa para gases ideales cuando se calientan o enfrían a presión constante en un proceso reversible.

Consideraciones importantes

• Las temperaturas siempre deben expresarse en kelvin (K) al usar estas fórmulas. Para convertir de grados Celsius a kelvin, se suma 273.15.

• Los procesos deben ser reversibles, es decir, deben ocurrir muy lentamente para que el sistema esté en equilibrio en todo momento.

• Las unidades del resultado son julios por kelvin (J/K).

• Estas fórmulas no aplican directamente a cambios de fase (como fusión o evaporación), para los cuales se debe usar otra expresión:

$\displaystyle \Delta S = \frac{Q_{\text{rev}}}{T}$

Donde $\displaystyle Q_{\text{rev}}$ es el calor de fusión o vaporización.

Ejercicios Resueltos de Entropía

Llegó el momento de practicar, vamos a resolver varios ejercicios para mejorar tu práctica sobre el tema, en algunos casos hemos consultado de buena bibliografía ejercicios que pueden ayudarte a comprender mejor el tema. ¿Estás listo?

Solución:

Usamos la fórmula del cambio de entropía para una sustancia con calor específico constante:

$\displaystyle \Delta S = m \cdot c \cdot \ln\left( \frac{T_f}{T_i} \right)$

Convertimos las temperaturas a kelvin:

$\displaystyle T_i = 25 + 273.15 = 298.15\ \text{K}$
$\displaystyle T_f = 75 + 273.15 = 348.15\ \text{K}$

Sustituimos:

$\displaystyle \Delta S = 2 \cdot 4186 \cdot \ln\left( \frac{348.15}{298.15} \right)$
$\displaystyle \Delta S = 8372 \cdot \ln(1.1678)$
$\displaystyle \Delta S = 8372 \cdot 0.1551 = 1298.7\ \text{J/K}$

Resultado:

$\displaystyle \Delta S \approx 1298.7\ \text{J/K}$

Solución:

Aplicamos la misma fórmula:

$\displaystyle \Delta S = m \cdot c \cdot \ln\left( \frac{T_f}{T_i} \right)$

Temperaturas en kelvin:

$\displaystyle T_i = 150 + 273.15 = 423.15\ \text{K}$
$\displaystyle T_f = 30 + 273.15 = 303.15\ \text{K}$

Sustituimos:

$\displaystyle \Delta S = 1.5 \cdot 500 \cdot \ln\left( \frac{303.15}{423.15} \right)$
$\displaystyle \Delta S = 750 \cdot \ln(0.7164)$
$\displaystyle \Delta S = 750 \cdot (-0.3337) = -250.3\ \text{J/K}$

Resultado:

$\displaystyle \Delta S \approx -250.3\ \text{J/K}$

Solución:

Para una expansión isotérmica de un gas ideal:

$\displaystyle \Delta S = n \cdot R \cdot \ln\left( \frac{V_f}{V_i} \right)$

Donde:

$n = 1\ \text{mol}$
$R = 8.314\ \text{J/mol·K}$
$V_f = 15\ \text{L}$
$V_i = 5\ \text{L}$

Sustituimos:

$\displaystyle \Delta S = 1 \cdot 8.314 \cdot \ln\left( \frac{15}{5} \right)$
$\displaystyle \Delta S = 8.314 \cdot \ln(3)$
$\displaystyle \Delta S = 8.314 \cdot 1.0986 = 9.13\ \text{J/K}$

Resultado:

$\displaystyle \Delta S \approx 9.13\ \text{J/K}$

Solución:

Usamos:

$\displaystyle \Delta S = n \cdot R \cdot \ln\left( \frac{V_f}{V_i} \right)$

Sustituimos:

$\displaystyle \Delta S = 2 \cdot 8.314 \cdot \ln\left( \frac{5}{20} \right)$
$\displaystyle \Delta S = 16.628 \cdot \ln(0.25)$
$\displaystyle \Delta S = 16.628 \cdot (-1.3863) = -23.05\ \text{J/K}$

Resultado:

$\displaystyle \Delta S \approx -23.05\ \text{J/K}$

Solución:

Usamos la fórmula para procesos a presión constante:

$\displaystyle \Delta S = n \cdot C_p \cdot \ln\left( \frac{T_f}{T_i} \right)$

Sustituimos:

$\displaystyle \Delta S = 1 \cdot \frac{7}{2} \cdot 8.314 \cdot \ln\left( \frac{600}{300} \right)$
$\displaystyle \Delta S = 29.099 \cdot \ln(2)$
$\displaystyle \Delta S = 29.099 \cdot 0.6931 = 20.17\ \text{J/K}$

Resultado:

$\displaystyle \Delta S \approx 20.17\ \text{J/K}$