Suma de Capacitores en Serie y Paralelo

Es importante que, al momento de comenzar este tema de la suma de capacitores o condensadores en serie, ya hayas leído acerca de la capacitancia y de como funcionan los capacitores de placas paralelas, porque utilizaremos algunas fórmulas para este tema.

Al igual que las resistencias, los capacitores son dispositivos que también podemos conectarlos en serie, en paralelo y de forma mixta e incluso combinadas con las resistencias, pero eso se verá en tópicos avanzados de ingeniería. Ahora lo que necesitamos comprender, es como poder relacionar a los capacitores para poder sumarlos tanto en serie como en paralelo

💡 ¿Cómo se suman los capacitores en Serie? 

Los capacitores si están en serie se suman de la siguiente manera:

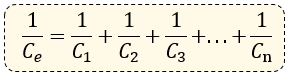
Es importante señalar que, en una conexión de capacitores en serie:

• La carga total de los capacitores, es la misma que se distribuye en cada capacitor.
• La diferencia de potencial total es la suma de cada diferencia de potencial de cada capacitor.

💡 ¿Cómo se suman los capacitores en Paralelo?

Si los capacitores se encuentran en paralelo, se suman de la siguiente manera:

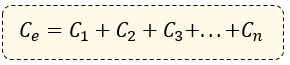
Aquí también es importante señalar que, en una conexión en paralelo:

• La carga total se obtiene sumando cada una de las cargas de los capacitores que están conectados.
• Los capacitores tendrán la misma diferencia de potencial cada uno.

🔸 Ejercicios Resueltos de Capacitores o Condensadores en Serie

Como es costumbre nuestra en el blog, para entender mucho mejor un tema de Física, recomendamos realizar y practicar ejercicios, para ello veremos algunos ejemplos de capacitores conectados en serie y en paralelo y así no tener problema alguno.

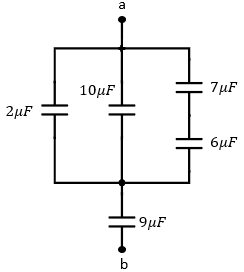
Solución:

En la imagen observamos 5 capacitores o condensadores que están conectados tanto en serie como en paralelo. Para que podamos encontrar la capacitancia equivalente debemos aprender que los capacitores que están seguidos uno de otro están en serie, tal como el capacitor de 7μF y el 6μF, por lo que lo podemos sumar.

a) Sumando capacitores en serie de 7μF y de 6μF

Si los capacitores están en serie, se suman de la siguiente forma:

$\displaystyle \frac{1}{{{C}_{7,6}}}=\frac{1}{7\mu F}+\frac{1}{6\mu F}=0.14+0.16=0.3\mu F$

Es decir:

$\displaystyle \frac{1}{{{C}_{7,6}}}=0.3\mu F$

Invirtiendo la igualdad:

$\displaystyle {{C}_{7,6}}=3.33\mu F$

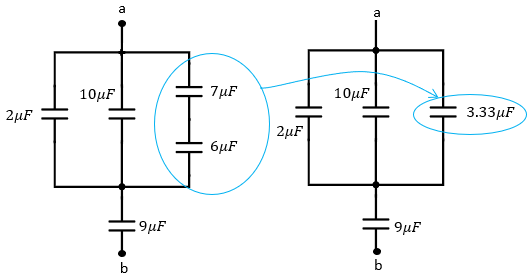
b) Sumando capacitores en paralelo de 2μF , 10μF y 3.33μF

Después de haber sumado en serie, obtenemos tres capacitores en serie, y para sumar en serie es muy fácil. Solamente sumamos:

$\displaystyle {{C}_{2,10,3.33}}=2\mu F+10\mu F+3.33\mu F=15.33\mu F$

Es decir que la suma de los tres capacitores en paralelo es de 15.33μF

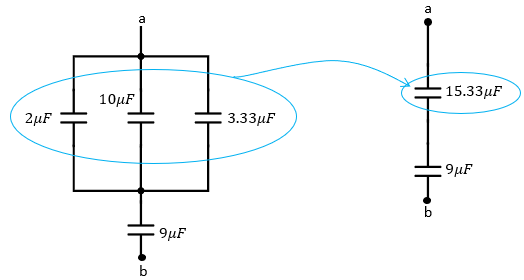
b) Sumando capacitores en serie de 15.33μF y 9μF

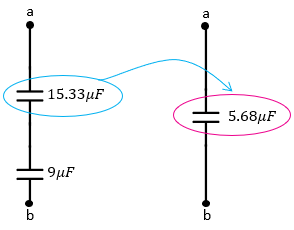
Finalmente nos quedan sumar dos resistencias en serie, una de 15.33μF y de 9μF. Para ello aplicamos la suma de capacitores en serie:

$\displaystyle \frac{1}{{{C}_{15.33,9}}}=\frac{1}{15.33\mu F}+\frac{1}{9\mu F}=0.065+0.111=0.176\mu F$

Es decir:

$\displaystyle \frac{1}{{{C}_{15.33,9}}}=0.176\mu F$

Invirtiendo la igualdad:

$\displaystyle {{C}_{15.33,9}}=\frac{1}{0.176}\mu F$

$\displaystyle {{C}_{15.33,9}}=5.68\mu F$

Es decir que la capacitancia final es de 5.68μF

Solución:

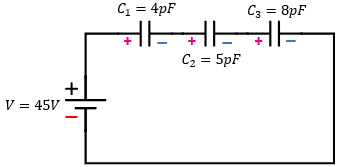
El problema y el diagrama nos describe a tres capacitores conectados en serie, para poder encontrar cada inciso, vamos a utilizar las fórmulas que hemos visto hasta este momento.

a) Calcular la capacitancia equivalente o total

Aplicamos la fórmula que vimos anteriormente, para sumar condensadores o capacitores en serie.

$\displaystyle \frac{1}{{{C}_{e}}}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}}+\frac{1}{{{C}_{3}}}$

Sustituyendo los valores de los capacitores:

Recordar que el pico-farad pF = x 10^(-12)

$\displaystyle \frac{1}{{{C}_{e}}}=\frac{1}{4pF}+\frac{1}{5pF}+\frac{1}{8pF}$

$\displaystyle \frac{1}{{{C}_{e}}}=0.25pF+0.2pF+0.125pF=0.575pF$

$\displaystyle \frac{1}{{{C}_{e}}}=0.575pF$

Invirtiendo la igualdad:

$\displaystyle \frac{1}{0.575pF}={{C}_{e}}$

Qué también la podemos reescribir de esta forma:

$\displaystyle {{C}_{e}}=\frac{1}{0.575}pF$

Resolviendo la división, obtenemos:

$\displaystyle {{C}_{e}}=1.74pF$

Por lo que la capacitancia equivalente es de 1.74pF

b) Encontrar la carga depositada en cada capacitor o condensador

Para que podamos encontrar la carga depositada en cada capacitor, debemos entender primero que se trata de una conexión en serie, por lo tanto la carga depositada en cada capacitor es la misma. Así que solamente aplicamos la fórmula de la capacitancia.

$ \displaystyle C=\frac{Q}{V}$

Despejando a "Q"

$\displaystyle Q=CV$

Sustituyendo el valor de la carga equivalente y de la diferencia de potencial, esto nos queda:

$\displaystyle Q=CV=\left( 1.74pF \right)\left( 45V \right)=78.3x{{10}^{-12}}C$

Por lo que obtenemos un total de carga de 78.3x10^(-12) Coulombs.

c) Obtener la diferencia de potencial en cada capacitor

En una conexión en serie, la diferencia de potencial de cada capacitor se calcula de manera individual, entonces aplicamos, la fórmula de la capacitancia, pero despejando a la diferencia de potencial.

$\displaystyle V=\frac{Q}{C}$

Aplicamos la fórmula para el primer capacitor o condensador:

$\displaystyle {{V}_{1}}=\frac{Q}{{{C}_{1}}}=\frac{78.3x{{10}^{-12}}C}{4x{{10}^{-12}}F}=19.575V$

Obtenemos una diferencia de potencial de 19.5 Volts

Ahora hacemos lo mismo para el segundo capacitor:

$\displaystyle {{V}_{2}}=\frac{Q}{{{C}_{2}}}=\frac{78.3x{{10}^{-12}}C}{5x{{10}^{-12}}F}=15.66V$

Obtenemos una diferencia de potencial de 15.7 Volts

Y hacemos también lo mismo para el tercer capacitor

$\displaystyle {{V}_{3}}=\frac{Q}{{{C}_{3}}}=\frac{78.3x{{10}^{-12}}C}{8x{{10}^{-12}}F}=9.7875V$

Y obtenemos una diferencia de potencial de 9.8 Volts

El voltaje total suministrado "V" es igual a la suma individual, es decir:

$\displaystyle V={{V}_{1}}+{{V}_{2}}+{{V}_{3}}=19.5V+15.7V+9.8V=45V$

Que es el valor de la fuente de 45 Volts.

Solución:

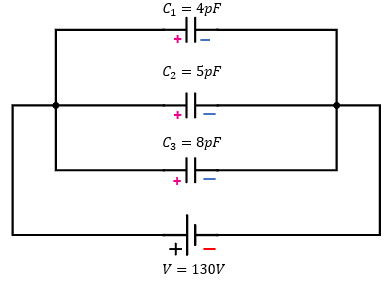
Si analizamos el diagrama, nos damos cuenta que se tratan de capacitores conectados en paralelo, dicho arreglo de capacitores están alimentados por una diferencia de potencial de 130 Volts, ahora es momento de resolver cada inciso.

a) Obtener la capacitancia equivalente

Observemos que los capacitores están en paralelo, por lo tanto la capacitancia equivalente se calcula con su fórmula:

$\displaystyle C={{C}_{1}}+{{C}_{2}}+{{C}_{3}}$

Sustituyendo el valor de cada capacitor en la fórmula:

$\displaystyle {{C}_{e}}=4pF+5pF+8pF=17pF$

Por lo que la capacitancia equivalente es de 17pF

b) Obtener la diferencia de potencial de cada capacitor o condensador

Al ser una conexión en paralelo, la diferencia de potencial de cada capacitor es la misma a la de la fuente. Es decir, que los tres capacitores tendrán una diferencia de potencial igual a 130 Volts. Por lo tanto:

$\displaystyle \begin{array}{l}{{V}_{1}}=130V\\{{V}_{2}}=130V\\{{V}_{3}}=130V\end{array}$

Por lo que la diferencia de potencial en todos los condensadores es de 130 Volts

c) La carga en cada capacitor o condensador

A diferencia de la conexión en serie, en la conexión en paralelo la carga se calcula de forma individual. De la siguiente manera:

$\displaystyle Q=VC$

Ahora calculemos la carga del primer capacitor:

$\displaystyle {{Q}_{1}}=V{{C}_{1}}=\left( 130V \right)\left( 4x{{10}^{-12}}F \right)=520x{{10}^{-12}}C$

Por lo que la carga en el primer capacitor es de 520x10^(-12) C

Ahora lo hagamos con el segundo capacitor:

$\displaystyle {{Q}_{2}}=V{{C}_{2}}=\left( 130V \right)\left( 5x{{10}^{-12}}F \right)=650x{{10}^{-12}}C$

De esta forma sabemos que la carga en el segundo capacitor es de 650x10^(-12) C

Y finalmente obtenemos el valor de la carga del tercer capacitor:

$\displaystyle {{Q}_{3}}=V{{C}_{3}}=\left( 130V \right)\left( 8x{{10}^{-12}}F \right)=1040x{{10}^{-12}}C$

Por lo que obtenemos un valor de 1040x10^(-12) C

d) La carga total almacenada por los capacitores

Para obtener este último valor, simplemente sumamos todas las cargas.

$\displaystyle Q={{Q}_{1}}+{{Q}_{2}}+{{Q}_{3}}$

Esto nos daría el siguiente valor

$\displaystyle Q=520x{{10}^{-12}}C+650x{{10}^{-12}}C+1040x{{10}^{-12}}C=2210x{{10}^{-12}}C$

Por lo que obtenemos un valor de la carga total de 2210x10^(-12) C

Qué también lo podemos escribir de esta forma:

$\displaystyle Q=2210x{{10}^{-12}}C=2.21x{{10}^{-9}}C=2.21nC$

Nota:

Si multiplicamos la capacitancia equivalente por la diferencia de potencial total obtendremos el mismo resultado de la carga total.

$\displaystyle Q={{C}_{e}}V=\left( 17x{{10}^{-12}}F \right)\left( 130V \right)=2210x{{10}^{-12}}C$