Capacitores o Condensadores - Ejercicios Resueltos
Después de entender por completo el tema de la Ley del Ohm, y como se deben sumar resistencias en serie y en paralelo, así como circuitos mixtos de resistencias. Existe también otros componentes de gran importancia que tenemos que aprender en Física, específicamente en el área de la electricidad, y ese es el estudio de los capacitores o condensadores. En este artículo tocaremos el tema de la capacitancia, más adelante veremos de que trata. ?
¿Qué es un capacitor o condensador?
La definición de lo que es un capacitor o condensador es muy sencilla, un capacitor eléctrico es un dispositivo que se emplea para almacenar cargas eléctricas. La forma más básica de un capacitor consta de dos láminas metálicas que están separadas por un aislante o material dieléctrico, que bien puede ser aire, vidrio, mica, aceite o cualquier otro tipo de material aislante.
La Capacitancia es la capacidad que tiene un capacitor para almacenar cierta cantidad de carga eléctrica. A la unidad de capacitancia se le da el nombre de farad (F) en honor al gran físico y químico Michael Faraday. Los capacitores son ampliamente utilizados en diversas aplicaciones, como en el flash de una cámara fotográfica, para almacenar energía en los cargadores de las laptops, para bloquear picos de carga eléctrica con la finalidad de proteger el circuito. Prácticamente todo sistema hoy en día utiliza capacitores.
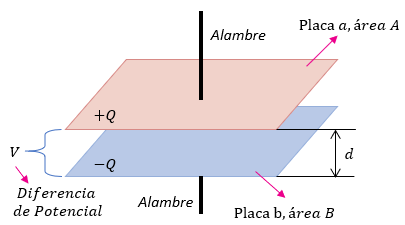
Como hemos dicho, un capacitor simple consiste en un par de placas paralelas de área A, separadas por una pequeña distancia d.
En los circuitos eléctricos, los capacitores los podemos encontrar de las siguiente forma, estos representan su diagrama o símbolo.
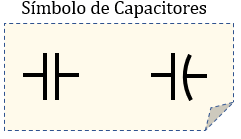
Veamos la imagen de abajo, si se aplica un voltaje a través de un capacitor que está conectado a una batería mediante cables conductores, las dos placas se cargan rápidamente, una placa adquiere carga negativa y la otra una carga positiva de la misma magnitud. Por lo que se dice que tanto la terminal de la batería, como las placas del capacitor están al mismo potencial. A menudo lo que le llamamos voltaje ahora le pasaremos a llamar "diferencia de potencial", que es exactamente lo mismo.
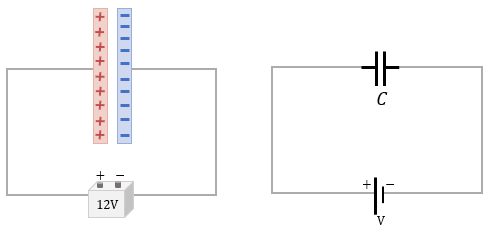
Como vemos que las placas están cargadas tanto con cargas positivas, así como las cargas negativas. Vemos que la cantidad de carga que adquiere las placas es proporcional a la magnitud de la diferencia de potencial "V" que se aplicó en las placas.
Q = CV
La constante de proporcionalidad la llamamos "C" que nos indica la capacitancia del capacitor. La unidad de capacitancia es el coulomb entre volt. Los capacitores ordinarios que podemos encontrar en cualquier tienda comercial de electrónica, son en rangos de capacidad de 1pF (picofarad = 10^(-12)), hasta 1μF (microfarad = 10^(-6)). En realidad existen muchos valores comerciales, pero el rango más común está entre microfarads y picofarads.
Tipos de Capacitores
Existen diversos tipos de capacitores y cada uno con una aplicación en particular pero con el mismo fin. Veamos algunos tipos de capacitores.

Otro tipo de capacitor muy frecuente en circuitos eléctricos, son los capacitores cerámicos.

Así también existen, los capacitores de poliéster.

Fórmula de la Capacitancia y de un Capacitor de Placas Paralelas
La fórmula principal de la capacitancia es la siguiente:
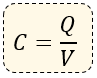
Dónde:
C = Capacitancia del capacitor (Unidades en Farad "F")
Q = Carga almacenada por el capacitor (Unidades en Coulombs "C")
V = Diferencia de potencial entre las placas del capacitor (Unidades en Volts "V")
Ahora, cuando deseamos calcular la capacitancia de un capacitor de placas paralelas como es el caso de este artículo, utilizaremos la siguiente expresión matemática o fórmula:
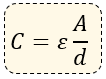
Dónde:
ε = Constante de la permitividad que depende del tipo de aislante.
A = Área de una de las placas paralelas (Unidades en Metros "m")
d = Distancia entre las placas paralelas (Unidades en Metros "m")
En este post, utilizamos el término de permitividad, donde la constante ε se le conoce como permitividad eléctrica o también llamada como permitividad del medio aislante, esta es igual al producto de la constante de la permitividad en el vacío por la permitividad relativa:
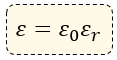
La constante de la permitividad en el vacío tiene el siguiente valor:
$\displaystyle {{\varepsilon }_{0}}=8.85x{{10}^{-12}}\frac{F}{m}$
Tabla de Permitividad de algunos medios
Ya que hemos hablado sobre la permitividad, veamos algunos datos de la permitividad relativa. ?
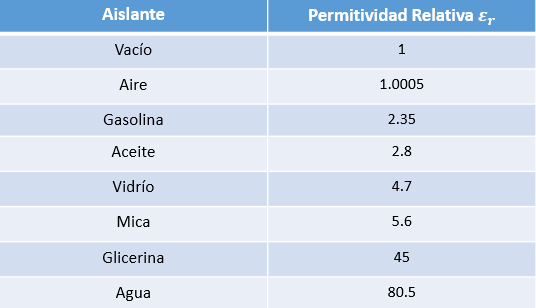
Estos datos son fundamentales para la resolución de problemas y ejemplos de Capacitancia.
Ejercicios Resueltos de Capacitores o Condensadores
Para profundizar mucho mejor el tema de capacitores o condensadores. Veamos algunos ejercicios de placas paralelas. ?
Solución:
A simple vista observamos que los datos están en el mismo problema, partiendo de la separación de 2 mm, así como el medio aislante qué es el aire, y las medidas de la placa. Para ello lo primero que haremos será recopilar nuestros datos:
Datos:
$\displaystyle d=2mm$
$\displaystyle A=12cm\times 15cm$
$\displaystyle {{\varepsilon }_{r(aire)}}=1$
$\displaystyle {{\varepsilon }_{0}}=8.85x{{10}^{-12}}\frac{F}{m}$
Primero debemos saber a cuánto equivale la permitividad, aplicamos la fórmula:
$\displaystyle \varepsilon ={{\varepsilon }_{0}}{{\varepsilon }_{r}}$
Sustituyendo nuestros datos en la fórmula, obtenemos:
$\displaystyle \varepsilon =\left( 1 \right)\left( 8.85x{{10}^{-12}}\frac{F}{m} \right)=8.85x{{10}^{-12}}\frac{F}{m}$
Ahora es momento de calcular el área de la placa, debemos de recordar que la medida debe ser en metros cuadrados.
$\displaystyle \begin{array}{l}12cm=0.12m\\15cm=0.15m\end{array}$
Ahora calculamos el área de las placas
$\displaystyle A=0.12m\times 0.15m=0.018{{m}^{2}}$
La distancia también debemos pasarla a metros.
$\displaystyle d=2mm\left( \frac{1m}{1000mm} \right)=0.002m$
a) Calcular la capacitancia del capacitor
$\displaystyle C=\varepsilon \frac{A}{d}$
Sustituyendo datos en la fórmula:
$\displaystyle C=\left( 8.85x{{10}^{-12}}\frac{F}{m} \right)\frac{0.018{{m}^{2}}}{\left( 0.002m \right)}=79.65x{{10}^{-12}}F$
Al ser una base de 10 elevado a la menos 12, también le podemos llamar "Pico". Es decir:
$\displaystyle C=\left( 8.85x{{10}^{-12}}\frac{F}{m} \right)\frac{0.018{{m}^{2}}}{\left( 0.002m \right)}=79.65pF$
Por lo que el valor del capacitor es de 79.65 pF
Resultado:
$\displaystyle C=79.65pF$
Solución:
A diferencia del ejemplo 1, en este problema contamos con un material como la mica que posee su propia permitividad relativa, nuevamente tenemos que reunir todos los datos necesarios para poder darle solución al ejercicio, en este caso empezaremos a utilizar todas las medidas de longitud en metros desde la recolección de los datos.
Datos:
$\displaystyle l=18cm\left( \frac{1m}{100cm} \right)=0.18m$
$\displaystyle d=0.05mm\left( \frac{1m}{1000mm} \right)=5x{{10}^{-5}}m$
$\displaystyle {{\varepsilon }_{r}}=5.6$
$\displaystyle {{\varepsilon }_{0}}=8.85x{{10}^{-12}}\frac{F}{m}$
a) Calcular la capacitancia del capacitor
Para llevar a cabo la solución del problema, recordemos que la permitividad tiene por fórmula:
$\displaystyle \varepsilon ={{\varepsilon }_{0}}{{\varepsilon }_{r}}$
Sustituimos los datos que tenemos, para obtener la permitividad:
$\displaystyle \varepsilon =\left( 8.85x{{10}^{-12}}\frac{F}{m} \right)\left( 5.6 \right)=4.956x{{10}^{-11}}\frac{F}{m}$
Ahora calculamos el área de las dos placas:
$\displaystyle A={{l}^{2}}={{\left( 0.18m \right)}^{2}}=0.0324{{m}^{2}}$
Aplicando la fórmula de la capacitancia:
$\displaystyle C=\varepsilon \frac{A}{d}=\left( 4.956x{{10}^{-11}}\frac{F}{m} \right)\left( \frac{0.0324{{m}^{2}}}{5x{{10}^{-5}}m} \right)=32.11x{{10}^{-9}}F$
Obtenemos un total de 32.11 nF es decir 32.11x10^(-9)F
Solución:
$\displaystyle C=32.11nF$
Ejercicios para Practicar de Capacitores o Condensadores
Ahora es momento de que practiques lo aprendido, a continuación se muestran algunos ejercicios resueltos paso a paso, para que puedas comprobar tus resultados. ??
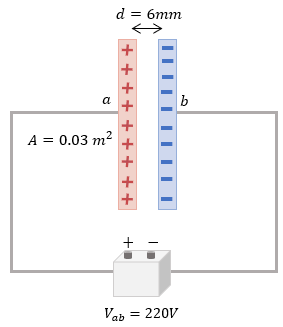
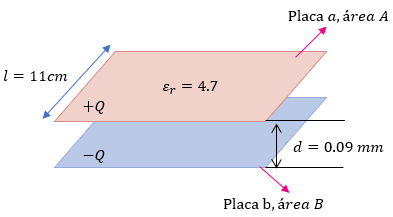
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
las placas de un capacitador de placas paralelas tienen una separación de 5 mm , entre las placas se encuentran un dieléctrico de Mica (Er=5,6). Calcular la capacitancia si cada placa circular mide 10 cm de diámetro . Dibuje el condensador con sus medidas
-
Excelente información . Sabe me acabo de inscribir en un curso de electrónica y me gusta mucha y si fuera necesario me gusta tener más información explisita como esta del resto de componentes porfavor.
-
Tengo una duda, la calculadora me da otro resultado en cuestion del punto, ya lo verifique varias veces pero aun desconozco el problema. ejemplo en el problema 2 de los ejemplos me sale 3.21148x10^(-8) y el resultado es 32.11×10^(-9)F alguien puede ayudarme?
-
Excelente información. Soy Instructor de la especialidad de Electricidad de Mantenimiento Industrial, en Venezuela.
-
Muy bueno tu trabajo !!!! FELICIDADES!!!!! les servirá de mucho a futuras generaciones y a toda la gente autodidacta.
37 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar