Variación de la Resistencia con la Temperatura

Para seguir comprendiendo el fenómeno de la Resistencia Eléctrica , y hacer uso de las leyes del ohm, o la resistividad de un material. Existe también un campo de estudio sobre la variación de la resistencia que tiene un material respecto a la temperatura. 😊💡

🌡La Variación de la Resistencia con la Temperatura

Es lógico pensar que la resistencia de cualquier material conductor aumenta su temperatura de forma proporcional cuando éste está expuesto. De forma muy experimental se ha demostrado que cuando alguien desea calcular la resistencia R de un conductor a una cierta temperatura T , si se conoce el valor de la resistencia R a una temperatura de 0°C, se puede utilizar la siguiente fórmula.

Dónde:

Rt = Resistencia del conductor a cierta temperatura T , (Expresada en Ohms "Ω" )

R0 = Resistencia del conductor en Ω a 0°C

α = Coeficiente de temperatura de la resistencia del material conductor en °C¯ ¹ , indica la variación relativa de la resistencia del material por cada grado centígrado de incremento en la temperatura.

T = Temperatura del conductor en °C

Se dice que en el caso de los metales α es siempre mayor que cero. ( α > 0 ). Pues su resistencia aumenta con la temperatura. A diferencia de otras sustancias como el carbono, silicio, y germanio, el valor de α es negativo, porque sus resistencia eléctrica disminuye con la temperatura. Veamos la siguiente tabla para entenderlo mejor:

⚡ Tabla de Coeficiente de Temperatura

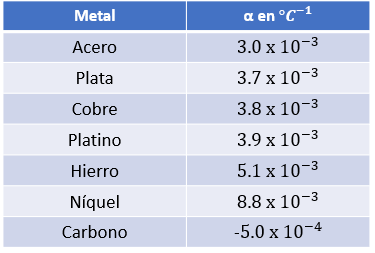
Note que el Carbono el valor de α es negativo.

Una de las grandes virtudes de este fenómeno ocurre cuando algunas sustancias alcanzan temperaturas muy bajas, podríamos decir que logran alcanzar el 0 K (cero absoluto), en ese punto la resistencia eléctrica de algunas metales es prácticamente cero, lo cual significa que los electrones libres se puedan desplazar sin dificultad a través de la red cristalina, esto produce el fenómeno que se conoce como Superconductividad eléctrica. 

🔸 Ejercicios Resueltos de Variación de la Resistencia con la Temperatura

Para entender mucho mejor el tema, pasemos a resolver ejercicios sobre este tema 😊

Solución:

En este ejercicio contamos con la resistencia inicial del cobre de 10Ω a 0°C, y nos piden encontrar el valor de la resistencia a 45°C, por lo que será muy sencillo de dar con el resultado.

Datos:

$\displaystyle {{\alpha }_{cobre}}=3.8x{{10}^{-3}}^{{}^\circ }{{C}^{-1}}$

$\displaystyle {{R}_{0}}=10\Omega $

$\displaystyle T=45{}^\circ C$

a) Obtener la resistencia a 45°C

De nuestra fórmula, obtenemos:

$\displaystyle {{R}_{T}}={{R}_{0}}\left( 1+\alpha T \right)$

Sustituyendo datos en la fórmula:

$\displaystyle {{R}_{T}}=10\Omega \left[ 1+\left( 3.8x{{10}^{-3}}^{^{{}^\circ }}{{C}^{-1}} \right)\left( 45{}^\circ C \right) \right]$

Realizando las operaciones indicadas:

$\displaystyle {{R}_{T}}=10\Omega \left( 1+0.171 \right)$

$\displaystyle {{R}_{T}}=10\Omega \left( 1.171 \right)$

Multiplicando:

$\displaystyle {{R}_{T}}=11.71\Omega $

Obtenemos que la resistencia a los 45°C serán de 11.71Ω

Solución:

Este problema requiere de analizar muy bien el planteamiento inicial del ejercicio, porque nos proporcionan inicialmente una resistencia de 9Ω a 190°C , es decir, ya sabemos cuanto vale la temperatura a cierta resistencia, lo que no sabemos es cuanto vale a 300°C. Para ello calculamos primero la resistencia inicial con los datos de que ya tenemos completos.

Datos:

$\displaystyle {{\alpha }_{platino}}=3.9x{{10}^{-3}}{}^\circ {{C}^{-1}}$

$\displaystyle {{R}_{190{}^\circ C}}=9\Omega $

$\displaystyle T=320{}^\circ C$

a) Obtener la resistencia a 320°C

De la fórmula:

$\displaystyle {{R}_{T}}={{R}_{0}}\left( 1+\alpha T \right)$

Despejamos a "R0" porque no lo tenemos, solo sabemos lo que vale la resistencia a 190°C

$\displaystyle {{R}_{0}}=\frac{{{R}_{T}}}{\left( 1+\alpha T \right)}$

Sustituyendo los datos en la fórmula:

$\displaystyle {{R}_{0}}=\frac{9\Omega }{\left[ 1+\left( 3.9x{{10}^{-3}}^{{}^\circ }{{C}^{-1}} \right)\left( 320{}^\circ C \right) \right]}$

Realizando las operaciones indicadas:

$\displaystyle {{R}_{0}}=\frac{9\Omega }{\left[ 1+\left( 3.9x{{10}^{-3}}^{{}^\circ }{{C}^{-1}} \right)\left( 320{}^\circ C \right) \right]}=\frac{9\Omega }{1+1.248}=4\Omega $

Ahora que sabemos que tenemos un valor cercano a los 4Ω , podemos calcular lo restante.

$\displaystyle {{R}_{T}}={{R}_{0}}\left( 1+\alpha T \right)$

Sustituyendo datos en la fórmula:

$\displaystyle {{R}_{T}}=4\Omega \left[ 1+\left( 3.9x{{10}^{-3}}^{{}^\circ }{{C}^{-1}} \right)\left( 320{}^\circ C \right) \right]$

Realizando las operaciones indicadas:

$\displaystyle {{R}_{T}}=4\Omega \left( 1+1.248 \right)=4\Omega \left( 2.248 \right)=8.992\Omega $

Por lo que nuestro resultado es de 8.992Ω un valor muy cercano a los 9Ω.