Conservación de la Energía Mecánica

Para poder hablar de la conservación de la energía mecánica, debemos pensar en la siguiente imagen y analizar lo que expresaremos en el siguiente párrafo.

energía mecánica

Podemos observar claramente que el tranvía posee energía cinética (porque están en movimiento) y energía potencial (porque están a cierta altura). La suma de las energías cinética y potencial de un sistema físico en relación con un marco de referencia por definición es su energía mecánica.

Si en el movimiento existe, además la participación del efecto producido por resortes o elásticos, entonces también debemos tener en cuenta la energía potencial elástica.

La naturaleza establece un principio muy importante con respecto a la energía: la cantidad total de energía existente en el universo permanece siempre igual, por lo tanto, no hay creación ni destrucción de la misma, sino solo su transformación, de una forma a otra. Así, se enuncia el Principio General de Conservación de Energía

Es importante señalar que, en ausencia de fuerzas disipativas (como la fricción y la resistencia del aire), la energía mecánica se conserva, permaneciendo constante. Pero las relaciones entre la energía cinética y potencial pueden variar, y una se convierte en la otra.

Contenidos

✅ Casos de Transformación de Energía Mecánica
📏 Fórmula de la Conservación de la Energía Mecánica
📄 Ejercicios Resueltos de Conservación de la Energía Mecánica

✅ Casos de Transformación de Energía Mecánica

Veamos tres casos muy importantes de la conservación de la energía mecánica y su transformación

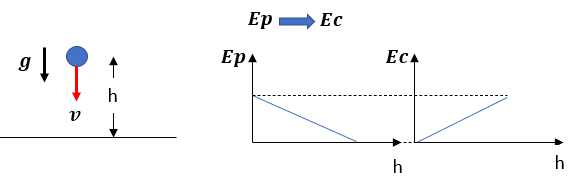
1️⃣ En la caída libre de un cuerpo, se pierde altura y se gana velocidad; la energía potencial se transforma continuamente en cinética.

conservación de la energía mecánica

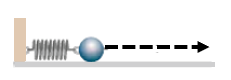
2️⃣ Al lanzar un proyectil, la energía elástica almacenada en el resorte se convierte en energía cinética. Con esto podemos saber cuál es la velocidad de salida del proyectil.

energía potencial elástica

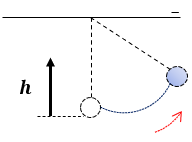
3️⃣ A medida que el péndulo oscila y gana altura, su velocidad disminuye y la energía cinética se transforma en energía potencial gravitacional; así que en el punto más alto el péndulo se detiene y la energía es toda potencial. Cuando el péndulo desciende, se produce el cambio contrario, hasta llegar al punto más bajo, donde la energía es toda cinética.

péndulo energía potencial

📏 Fórmula de la Conservación de la Energía Mecánica

La fórmula principal para este tema, es la siguiente:

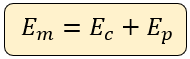
fórmula de la conservación de la energía mecánica

Dónde:

Em = Energía Mecánica (Joules)

Ec = Energía Cinética (Joules)

Ep = Energía Potencial (Joules)

Es común que el proceso de la energía mecánica permanezca constante durante el movimiento del objeto o partícula, por ello podemos enunciar la fórmula de la siguiente manera:

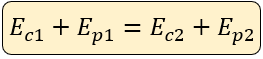
fórmula de la energía mecánica

La energía cinética inicial y la potencial gravitatoria inicial, serán iguales a la energía cinética final junto a la energía potencial gravitatoria final.

📄 Ejercicios Resueltos de Conservación de la Energía Mecánica

Veamos algunos ejemplos para comenzar a entender este tema 😀

Problema 1. Un carro de 200 g de masa, baja por una trayectoria como se muestra en la figura. Colocado a 50 cm respecto al suelo, el carro tiene una velocidad de 2 m/s. Sin tener en cuenta las fuerzas disipativas, ¿Qué altura tendrá cuando su velocidad sea de 3 m/s?

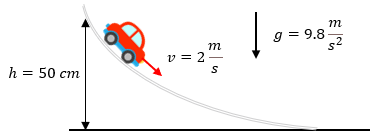
conservacion_energia_mecanica_problema_1

Solución:

La energía mecánica del carro es constante, ya que el sistema se considera conservativo. En ambas posiciones (llamemos al punto 1 el punto de altura 50 cm = 0,5 m y el punto 2 al punto de la altura solicitada por el problema) las energías mecánicas son iguales:

$\displaystyle E{{c}_{1}}+E{{p}_{1}}=E{{c}_{2}}+E{{p}_{2}}$

Anotemos nuestros datos:

🔔 Datos:

m1 = m2 = 50 g = 0.05 kg

g = 9.8 m/s^2

v1 = 2 m/s

h1 = 50 cm = 0.5 m

v2 = 3 m/s

h2 = ?

Si sabemos entonces que:

$\displaystyle E{{c}_{A}}+E{{p}_{A}}=E{{c}_{B}}+E{{p}_{B}}$

Es decir:

$\displaystyle \frac{1}{2}m{{v}_{1}}^{2}+mg{{h}_{1}}=\frac{1}{2}m{{v}_{2}}^{2}+mg{{h}_{2}}$

Dividimos todo entre "m" ya que la masa es la misma en ambos miembros:

$\displaystyle \frac{1}{2}{{v}_{1}}^{2}+g{{h}_{1}}=\frac{1}{2}{{v}_{2}}^{2}+g{{h}_{2}}$

Ahora vamos a sustituir nuestros datos en la fórmula:

$\displaystyle \frac{1}{2}{{\left( {2\frac{m}{s}} \right)}^{2}}+\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)\left( {0.5m} \right)=\frac{1}{2}{{\left( {3\frac{m}{s}} \right)}^{2}}+\left( {9.8} \right){{h}_{2}}$

Multiplicando lo que tenemos en las operaciones, nos queda:

$\displaystyle 2+4.9=4.5+\left( {9.8} \right){{h}_{2}}$

$\displaystyle 6.9=4.5+\left( {9.8} \right){{h}_{2}}$

$\displaystyle 6.9-4.5=\left( {9.8} \right){{h}_{2}}$

$\displaystyle 2.4=\left( {9.8} \right){{h}_{2}}$

diviendo a 2.4 por 9.8 para obtener la altura 2

$\displaystyle {{h}_{2}}=\frac{{2.4}}{{9.8}}=0.245m$

lo que vendría a ser una altura de 0.245 metros = 24.5 cm

Problema 2. Un clavadista de masa "m" se lanza desde un trampolín a 10 metros sobre la superficie del agua, como lo muestra la imagen. Utilice la conservación de la energía mecánica para hallar su rapidez a 5 metros sobre la superficie del agua, desprecie la resistencia del aire

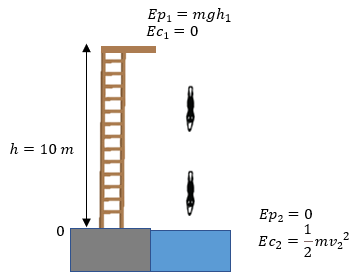
problema 2 de conservación de la energía mecánica

Solución:

Mientras el nadador cae sobre el agua, la única fuerza que actúa sobre él, es la fuerza de gravedad (la energía mecánica del sistema se conserva); además también podemos observar que mientras se lanza del trampolín lo hace en caída libre, lo que implica que la velocidad inicial sea cero, entonces esto hace que tengamos los datos necesarios para su solución:

Anotando los datos:

🔔 Datos:

m1 = m2

g = 9.8 m/s²

v1 = 0 m/s (en caída libre)

h1 = 10 m (altura del trampolín)

h2 = 5 m (altura pedida por el problema respecto a la superficie del agua)

v2 = ?

Utilizando la fórmula de la conservación de la energía mecánica

$\displaystyle E{{c}_{1}}+E{{p}_{1}}=E{{c}_{2}}+E{{p}_{2}}$

$\displaystyle \frac{1}{2}m{{v}_{1}}^{2}+mg{{h}_{1}}=\frac{1}{2}m{{v}_{2}}^{2}+mg{{h}_{2}}$

sustituyendo nuestros datos:

$\displaystyle \frac{1}{2}m{{\left( 0 \right)}^{2}}+m\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)\left( {10m} \right)=\frac{1}{2}m{{v}_{2}}^{2}+m\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)\left( {5m} \right)$

simplificando

$\displaystyle m\left( {98} \right)=\frac{1}{2}m{{v}_{2}}^{2}+m\left( {49} \right)$

Dividimos todo por "m" ya que son las mismas masas en ambos casos:

$\displaystyle 98=\frac{1}{2}{{v}_{2}}^{2}+49$

Aplicamos un poco de álgebra:

$\displaystyle 98-49=\frac{1}{2}{{v}_{2}}^{2}$

$\displaystyle 49=\frac{1}{2}{{v}_{2}}^{2}$

$\displaystyle 2\left( {49} \right)={{v}_{2}}^{2}$

$\displaystyle 98={{v}_{2}}^{2}$

$\displaystyle {{v}_{2}}^{2}=98$

Obteniendo la raíz cuadrada:

$\displaystyle {{v}_{2}}=\sqrt{{98}}=9.899\approx 9.9\frac{m}{s}$

Que vendría a ser nuestra velocidad final 9.9 m/s

Nota: Observe que el resultado no depende de la masa del clavadista.

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

9 Comentarios Publicados

Vicente dice:

5 julio, 2022 a las 1:03 pm

Cómo se puede explicar el 2(49)=V2

Responder
José Mercado dice:

4 septiembre, 2022 a las 1:53 pm

Me encanta como explican la resolución de los ejercicios, fácil, sencillo entendibles

Responder
1. Carlos julián dice:
  
  16 septiembre, 2022 a las 8:47 am
  
  Muchas gracias José!
  
  Responder
Antonio Castro dice:

21 septiembre, 2022 a las 10:51 pm

del ejercicio2. Cómo se calcularía el valor de "m" ?

Responder
euclides quito dice:

26 junio, 2023 a las 11:54 pm

exelente es de suma ayuda

Responder
jesed dice:

30 junio, 2023 a las 10:41 am

hola Carlos, como se encuentra la velocidad en la altura 5m? en el probelama del nadador

Responder
Melissa Arias dice:

16 agosto, 2023 a las 12:50 am

Es de mucha ayuda estos ejercicios

Responder
Josue dice:

21 agosto, 2023 a las 12:42 pm

en Cuerpo cilindrico Cae desde una altura de 8m Con velocidad inicial de 0m/s en el punto 1, La masa del objeto es de 500g. Calcular la energia Em, Ec y Ep en el punto 2 a 4m de altura . punto 3.Cuando el objeto allegado al suelo

Responder
Luis de la puente dice:

26 febrero, 2024 a las 6:27 pm

Me encanta ya q me ayuda mucho a mejorar en lo que no entiendo y por medio de ella también puedo ASER muchas tareas y pues en pocas palabras me encanta mucho 🙈

Responder

Deja una respuesta Cancelar la respuesta