Límites Trigonométricos Indeterminados - Ejercicios Resueltos

Hoooola!, hoy hablaremos de un tema que se conoce como límites, pero no nos enfocaremos en su definición, ni en su explicación informal con épsilon-delta, sino que hablaremos de la parte algebraica, y trigonométrica para poder hacer artificios matemáticos (no magia), que nos ayuden a resolver problemas de indeterminación, y eso es muy importante, ya que si un límite se nos indetermina tenemos que buscar la solución.

Así que antes de comenzar, te voy a sugerir que descargues la siguiente lista de identidades trigonométricas que hemos hecho con cariño para ti 😎

⭕ Tabla de Límites Notables 

Eso no es todo, también es necesario tener en cuenta los límites notables, y saber en que momento aplicarlos, para ello colocaré los que más se usan, si conoces más, es porque muchos se deducen de los aquí propuestos.

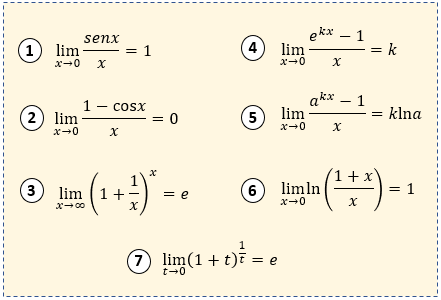
Si ya has descargado el material, y tienes en cuenta los límites notables entonces es momento de ver unos ejemplos resueltos:

🔸 Ejemplos de Límites Indeterminados Trigonométricos 0/0

Problema 1.- Resolver el siguiente límite trigonométrico

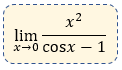
Solución:

Como el tema que estamos viendo es sobre indeterminación de la forma 0/0, es lógico que al evaluar obtengamos la indeterminación, así que lo primero que haremos es pensar un poco en lo que tenemos y tener en cuenta que si tenemos:

$\displaystyle \cos x-1$

Lo más accesible, es recurrir a su complemento para formar una diferencia de cuadrados en el denominador pues es más fácil llegar así a un límite notable, entonces hacemos lo siguiente:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}}{\cos x-1}\cdot \frac{\cos x+1}{\cos x+1}$

Haciendo la operación, tenemos.

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}}{\cos x-1}\cdot \frac{\cos x+1}{\cos x+1}=\underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}\left( \cos x+1 \right)}{{{\cos }^{2}}-1}$

De la identidad pitagórica nosotros observamos que:

$\displaystyle se{{n}^{2}}x+{{\cos }^{2}}x=1$

Despejando a seno cuadrado de x.

$\displaystyle se{{n}^{2}}x=1-{{\cos }^{2}}x$

Pero esto no se parece a lo que obtuvimos en el denominador de nuestro límite, peeeeero hay una solución y eso es factorizar el signo para que el límite nos quede de la siguiente forma:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}\left( \cos x+1 \right)}{-\left( 1-{{\cos }^{2}}x \right)}$

Ahora hacemos el cambio por seno cuadrado de x.

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}\left( \cos x+1 \right)}{-\left( 1-{{\cos }^{2}}x \right)}=\underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}\left( \cos x+1 \right)}{-se{{n}^{2}}x}=-\underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}\left( \cos x+1 \right)}{se{{n}^{2}}x}$

Por los límites notables, sabemos que:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{senx}{x}=1$

Aplicamos entonces la división de nuestro límite por $\displaystyle {{x}^{2}}$

$\displaystyle -\underset{x\to 0}{\mathop{\lim }}\,\frac{\frac{{{x}^{2}}\left( \cos x+1 \right)}{{{x}^{2}}}}{\frac{se{{n}^{2}}x}{{{x}^{2}}}}=-\underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x+1}{\frac{se{{n}^{2}}x}{{{x}^{2}}}}$

Y esto lo podemos aplicar de la siguiente forma:

$\displaystyle -\frac{\underset{x\to 0}{\mathop{\lim }}\,\left( \cos x+1 \right)}{\underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}}}=-\frac{2}{1}=-2$

Por lo que la respuesta de nuestro límite es -2.

Respuesta:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}}{\cos x-1}=-2$

Problema 2.- Resolver el siguiente límite trigonométrico

Solución:

Cómo sabemos que la inversa de el coseno es la secante, y como se trata de cero, entonces nos dará 1 de la misma forma, por lo que el límite nuevamente se indetermina, como era de esperarse, ahora para poder darle solución a este haremos lo siguiente. "Cambiar todo a Cosenos".

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{1-\sec x}{{{x}^{2}}\sec x}=\frac{1-\frac{1}{\cos x}}{{{x}^{2}}\frac{1}{\cos x}}$

y haremos la resta de fracciones del numerador:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{1-\sec x}{{{x}^{2}}\sec x}=\frac{1-\frac{1}{\cos x}}{{{x}^{2}}\frac{1}{\cos x}}=\frac{\frac{\cos x-1}{\cos x}}{\frac{{{x}^{2}}}{\cos x}}$

Aplicando la ley de la torta-herradura 😀

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{1-\sec x}{{{x}^{2}}\sec x}=\frac{1-\frac{1}{\cos x}}{{{x}^{2}}\frac{1}{\cos x}}=\frac{\frac{\cos x-1}{\cos x}}{\frac{{{x}^{2}}}{\cos x}}=\frac{\cos x(\cos x-1)}{\cos x\cdot {{x}^{2}}}$

Simplificando

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x(\cos x-1)}{\cos x\cdot {{x}^{2}}}=\underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{{{x}^{2}}}$

Y este límite va obteniendo una forma similar al del ejemplo 1, y al multiplicarlo por su conjugado obtenemos lo siguiente:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{{{x}^{2}}}\cdot \frac{\cos x+1}{\cos x+1}=\frac{{{\cos }^{2}}x-1}{{{x}^{2}}\left( \cos x+1 \right)}$

Fácilmente hacemos el cambio por la identidad pitagórica

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}\left( \cos x+1 \right)}$

Luego hacemos...

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}\left( \cos x+1 \right)}=\underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}}\cdot \underset{x\to 0}{\mathop{\lim }}\,\frac{1}{\cos x+1}$

Y evaluamos

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}}\cdot \underset{x\to 0}{\mathop{\lim }}\,\frac{1}{\cos x+1}=(1)\cdot \underset{x\to 0}{\mathop{\lim }}\,\frac{1}{\cos x+1}=1\cdot \frac{1}{2}=\frac{1}{2}$

Esto quiere decir que nuestro límite es 1/2

Respuesta:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{1-\sec x}{{{x}^{2}}\sec x}=\frac{1}{2}$

Problema 3.- Resolver el siguiente límite trigonométrico

Solución:

Al plantearse el problema anterior, y sabiendo que podemos pasar la función cosecante a seno, tenemos entonces:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{3{{x}^{3}}{{\csc }^{2}}x}=\frac{\cos x-1}{3{{x}^{3}}\cdot \frac{1}{se{{n}^{2}}x}}=\frac{\cos x-1}{\frac{3{{x}^{3}}}{se{{n}^{2}}x}}$

Ahora aplicamos la ley de la torta

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{\frac{3{{x}^{3}}}{se{{n}^{2}}x}}=\underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x\left( \cos x-1 \right)}{3{{x}^{3}}}$

Podemos hacer que la x que está al cubo, se haga como el producto de x al cuadrado por x, y obtenemos

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{\frac{3{{x}^{3}}}{se{{n}^{2}}x}}=\underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x\left( \cos x-1 \right)}{3{{x}^{2}}\cdot x}=\frac{1}{3}\underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}}\cdot \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{x}$

Pero de aquí podemos observar lo siguiente

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{x}=\underset{x\to 0}{\mathop{\lim }}\,\frac{-\left( 1-\cos x \right)}{x}=-\left( 0 \right)=0$

Por lo que nuestro límite converge en cero.

Respuesta:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{3{{x}^{3}}{{\csc }^{2}}x}=0$