Suma de Vectores - Método del Polígono [Ejercicios Resueltos]
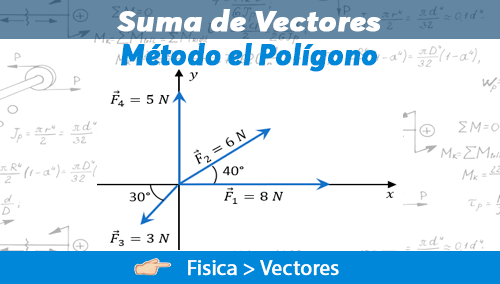
Como vimos en el tema anterior de Vectores, en la suma de vectores por el método analítico entre dos vectores. También puede darse el caso que en la suma no solamente existan dos vectores, sino más vectores concurrentes o angulares y necesitemos calcular el vector resultante, así como su ángulo. Para ello se lleva a cabo el siguiente método.
Método del Polígono
El Método del Polígono lo podemos encontrar de dos formas, por medio del método gráfico o por medio del método analítico, en nuestro sitio web solamente hablaremos del método analítico, ya que para el método gráfico es necesario tener una regla, un transportador y una escala para determinar la resultante y el ángulo, pero en este caso solamente nos interesan los cálculo.
De forma Gráfica
Cuando se trata de un problema de suma de vectores por el método gráfico, los vectores se tienen que colocar paralelamente a si mismos a los vectores que se irán sumando, del tal forma que uno de los vectores será la base, y los demás se irán colocando uno detrás de otro hasta llegar al último vector.
[alert-note]La resultante será el vector que una el origen de los vectores con la punta del último vector, y su sentido estará orientado hacia el extremo del último vector [/alert-note]
Veamos un ejemplo de manera gráfica, asumiendo que tenemos 4 vectores:
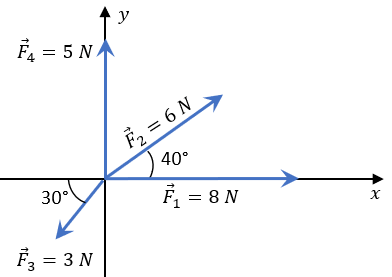
Para sumar los 4 vectores, los podemos colocar de la manera que querramos, no necesariamente seguir (1, 2, 3 y 4), puede ser que primero tomemos al vector 4 como primero, y así sucesivamente.
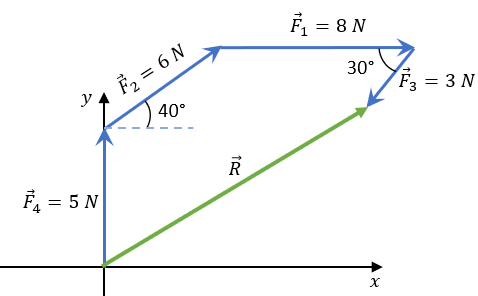
Sin embargo, para poder obtener un resultado más exacto, es necesario tener qué usar el método analítico.
El método analítico
Para realizar el método analítico necesitamos realizar los siguientes pasos:
1.- Descomponer en componentes rectangulares cada vector
2.- Una vez descomponiendo cada vector, es importante hacer la suma de componentes en "x" y "y" para cada vector, de tal forma que los vectores se reduzcan a un valor resultante en "x" y un valor resultante en "y" con esto lograremos obtener el valor de la resultante final.
3.- Utilizar el teorema de pitágoras para encontrar la magnitud resultante de los dos vectores perpendiculares.
4.- Utilizar la función tangente para calcular el ángulo de la resultante respecto a la horizontal.
Ejercicios Resueltos de Método Analítico (Polígono)
Imaginando que deseamos resolver el ejercicio anterior, tendríamos que analizar los 4 vectores, de esta forma:
Analizando el Vector F1
El vector F1 es un vector horizontal, que no posee ninguna componente en el eje "y", solamente en el eje "x" con esto podemos tener el primer valor para "x" una magnitud de 8N.
$\displaystyle {{F}_{1x}}=8N$
Analizando el Vector F2
El vector F2 tiene una magnitud de 6 N, y 40°, es decir; que posee componentes tanto en "x" como en "y", entonces lo descomponemos mediante las funciones trigonométricas correspondientes:
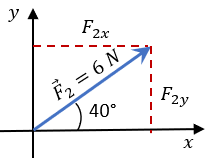
$\displaystyle {{F}_{2}}_{x}={{F}_{2}}\cos (40{}^\circ )=6\cos (40{}^\circ )=4.596N$
$\displaystyle {{F}_{2}}_{y}={{F}_{2}}sen(40{}^\circ )=6sen(40{}^\circ )=3.856N$
Analizando el Vector F3
Lo que podemos observar de este vector, es que está en el cuarto cuadrante y con 30° respecto a la horizontal, por lo que sus componentes serán negativos tanto para "x" como para "y"
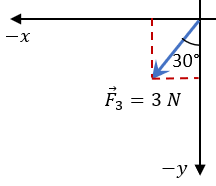
$\displaystyle {{F}_{3}}_{x}={{F}_{3}}cos(30{}^\circ )=3\cos (30{}^\circ )=2.598N$
$\displaystyle {{F}_{3y}}={{F}_{3}}sen(30{}^\circ )=3sen(30{}^\circ )=1.5N$
Lo único que haremos será cambiar de signo a los valores de las componentes
$\displaystyle {{F}_{3}}_{x}=-2.598N$
$\displaystyle {{F}_{3y}}=-1.5N$
Analizando el Vector F4
Este vector es un vector vertical, por lo que solamente tiene componentes en el eje "y", es decir una magnitud de 5N
$\displaystyle {{F}_{4y}}=5N$
Calculando la sumatoria de fuerzas en el eje "x"
$\displaystyle {{R}_{x}}=\sum{{{F}_{x}}}={{F}_{1x}}+{{F}_{2x}}-{{F}_{3x}}$
$\displaystyle {{R}_{x}}=8N+4.596N-2.598N=9.998N$
Calculando la sumatoria de fuerzas en el eje "y"
$\displaystyle {{R}_{y}}=\sum{{{F}_{y}}}={{F}_{2y}}-{{F}_{3y}}+{{F}_{4y}}$
$\displaystyle {{R}_{y}}=3.856N-1.5N+5N=7.356N$
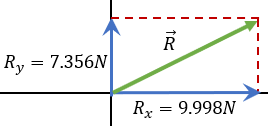
Obteniendo la resultante
Aplicando el teorema de pitágoras
$\displaystyle R=\sqrt{{{R}_{x}}^{2}+{{R}_{y}}^{2}}$
$\displaystyle R=\sqrt{{{\left( 9.998N \right)}^{2}}+{{\left( 7.356N \right)}^{2}}}$
$\displaystyle R=\sqrt{154.07{{N}^{2}}}$
Por lo que
$\displaystyle R=12.41N$
Qué sería nuestra magnitud.
Obteniendo el ángulo de la resultante:
Aplicamos la tangente (cateto opuesto/cateto adyacente) para obtener el ángulo.
$\displaystyle \tan \alpha =\frac{{{R}_{y}}}{{{R}_{x}}}=\frac{7.356N}{9.998N}=0.736$
aplicamos el arcotangente
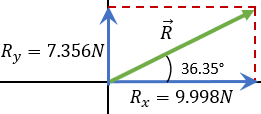
$\displaystyle \alpha ={{\tan }^{-1}}(0.736)=36.35{}^\circ $
Por lo que tendríamos un ángulo de 36.35° de la resultante respecto a la horizontal.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
me pueden ayudar pero con problemas pero resueltos
-
Me pueden ayudar con esto.
De la punta del vector A sale el vector B de la punta del vector B sale del vector C de la punta del vector C sale del vector D
Tengo estos datos A 40 km N, B 30 km 110o, C 50 km 30o, D 40 km 30o -
Hola, me podrían ayudar con mi tarea,
una lancha de motor efectúa los siguientes desplazamientos:
400 m al oeste, 600 pies al norte, 0.35 km al noreste y 150 yardas al sur -
hola,me pueden ayudar,con suma de 4 y 5 fuerzas,metodo paralelogramo.gracias
-
SERIAN 9
-
-
solicito me ayuden con tutoria en los siguientes casos, como suma de vectores
A=(12kgf; 330°)
B=(10kgf ;NO)
C=8kgf(-0,75i-0,25j)
por metodos:
de paralelogram
de poligono
algebraico en terminos de los vectores base
escrebir el vector resultante en cordenadas polares
escribir el vector resultante en coordenadas geograficas
escribir en vector resultante en funcion del vector unitario y su modulo-
Hallar el desplazamiento de 7km hacia el norte y 9km hacia el este
-
Suma de vectores por el método analógico utilizando el teorema de pitagoras y funciones trigonométricas
Hallar el desplazamiento de 7km hacia el norte y 9km hacia el este
-
34 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar