Tablas de Frecuencias para Datos no Agrupados - Ejercicios Resueltos
¡Hola, qué tal amigos de Fisimat! 👋 ¿Alguna vez te has encontrado con una montaña de números y no sabes por dónde empezar? ¡No te preocupes! Hoy vamos a desentrañar uno de los secretos mejor guardados para organizar y entender datos: las tablas de frecuencias para datos no agrupados. Esta herramienta es el primer paso para convertir el caos numérico en información clara y poderosa. 📊
En el mundo de la probabilidad y la estadística, antes de poder hacer predicciones complejas o aplicar modelos sofisticados, necesitamos ordenar nuestra casa. Las tablas de frecuencias son como el armario perfectamente organizado de un científico de datos: cada pieza de información tiene su lugar, es fácil de encontrar y nos cuenta una historia. Acompáñame en este viaje para dominar esta técnica fundamental, que te abrirá las puertas a un análisis de datos mucho más profundo. ¡Empecemos! 🚀
¿Qué son los Datos no Agrupados y por qué nos importan?
Antes de sumergirnos en las tablas, es crucial entender con qué tipo de material estamos trabajando. En estadística, los datos son la materia prima, y pueden presentarse de dos formas principales: agrupados y no agrupados.
Los datos no agrupados son simplemente los datos tal y como se han recogido, en su estado original. Son una lista de números, observaciones o mediciones que aún no han sido clasificados ni organizados en categorías o intervalos. Imagina que preguntas la edad a 20 personas en una sala; la lista de esas 20 edades es un conjunto de datos no agrupados.
Datos no Agrupados
Los datos no agrupados son el conjunto de datos que no han sido clasificados ni resumidos en intervalos o clases. Se presentan como una lista individual de observaciones. Son más manejables cuando el número de datos distintos no es muy grande (generalmente, menos de 20 o 30 valores diferentes).
Trabajar con datos no agrupados es ideal cuando tenemos un conjunto de datos relativamente pequeño o cuando la variedad de valores no es extensa. Nos permite ver cada valor individualmente y no perder detalle, lo cual es fundamental para el análisis exploratorio inicial. La tabla de frecuencias es nuestra mejor aliada para poner orden en esta lista inicial de datos.
Anatomía de una Tabla de Frecuencias: Conociendo sus Componentes
Una tabla de frecuencias es mucho más que una simple tabla con números. Es una herramienta estructurada que resume la distribución de los datos. Nos muestra cuántas veces aparece cada valor en nuestro conjunto de datos. Vamos a desglosar cada uno de sus componentes clave. 🕵️♂️
Frecuencia Absoluta (fi)
Es el componente más básico y fundamental. La frecuencia absoluta nos dice, literalmente, cuántas veces se repite cada valor específico en nuestro conjunto de datos.
Frecuencia Absoluta (fi)
La frecuencia absoluta, denotada como \(f_i\), es el número de veces que aparece un determinado valor \(x_i\) en un estudio estadístico. La suma de todas las frecuencias absolutas es igual al número total de datos, que se representa por \(N\). \[ \sum_{i=1}^{n} f_i = N \]
Por ejemplo, si estamos analizando las calificaciones de un examen y la nota "8" aparece 5 veces, la frecuencia absoluta del valor "8" es 5.
Frecuencia Relativa (hi)
Mientras que la frecuencia absoluta nos da un conteo, la frecuencia relativa nos da una proporción o un porcentaje. Nos ayuda a entender qué parte del total representa cada valor. Es especialmente útil para comparar distribuciones de datos con diferentes tamaños totales.
Frecuencia Relativa (hi)
La frecuencia relativa, denotada como \(h_i\), es el cociente entre la frecuencia absoluta de un determinado valor y el número total de datos. Se puede expresar como una fracción, un decimal o un porcentaje. \[ h_i = \frac{f_i}{N} \] La suma de todas las frecuencias relativas es siempre igual a 1 (o 100% si se expresa en porcentaje). \[ \sum_{i=1}^{n} h_i = 1 \]
Siguiendo el ejemplo anterior, si hay un total de 20 calificaciones, la frecuencia relativa de la nota "8" sería \(5/20 = 0.25\) o 25%.
Frecuencia Absoluta Acumulada (Fi)
Esta frecuencia nos da una perspectiva acumulativa. Nos dice cuántos datos son menores o iguales a un valor determinado. Es como ir sumando las frecuencias a medida que avanzamos por los valores ordenados de nuestros datos.
Frecuencia Absoluta Acumulada (Fi)
La frecuencia absoluta acumulada, denotada como \(F_i\), es la suma de las frecuencias absolutas de todos los valores iguales o inferiores al valor considerado. Se calcula sumando la frecuencia absoluta de un valor a la frecuencia absoluta acumulada del valor anterior. \[ F_i = f_1 + f_2 + \dots + f_i = \sum_{k=1}^{i} f_k \] El último valor de la frecuencia absoluta acumulada debe ser igual al número total de datos, \(N\).
Esta medida es fundamental para calcular percentiles y medianas.
Frecuencia Relativa Acumulada (Hi)
De manera similar a la anterior, esta frecuencia acumula las proporciones. Nos dice qué porcentaje de los datos es menor o igual a un valor determinado.
Frecuencia Relativa Acumulada (Hi)
La frecuencia relativa acumulada, denotada como \(H_i\), es el cociente entre la frecuencia absoluta acumulada de un determinado valor y el número total de datos. También se puede calcular sumando las frecuencias relativas. \[ H_i = \frac{F_i}{N} = \sum_{k=1}^{i} h_k \] El último valor de la frecuencia relativa acumulada es siempre 1 (o 100%).
Entender estos cuatro componentes es la clave para no solo construir, sino también para interpretar correctamente una tabla de frecuencias.
John Graunt
1620-1674
A menudo considerado el padre de la demografía y uno de los pioneros de la estadística, John Graunt, un mercero londinense, fue el primero en utilizar análisis estadísticos para estudiar los "Bills of Mortality" (Registros de Mortalidad) de Londres. En su obra de 1662, "Natural and Political Observations Mentioned in a Following Index, and Made upon the Bills of Mortality", Graunt organizó los datos de mortalidad en tablas, una forma primitiva de las tablas de frecuencias. Su trabajo sentó las bases para el uso de datos numéricos para comprender fenómenos sociales y de salud pública, demostrando que se podían extraer conclusiones significativas a partir de datos brutos organizados de manera sistemática. 😮
Construcción de una Tabla de Frecuencias Paso a Paso 🛠️
Ahora que conocemos las piezas, ¡es hora de construir! Crear una tabla de frecuencias para datos no agrupados es un proceso metódico y sencillo. Sigamos estos pasos y verás qué fácil es.
- Recopilar y Ordenar los Datos: El primer paso es tener todos tus datos. Una vez que los tienes, ordénalos de menor a mayor. Esto facilita enormemente el conteo y evita errores.
- Identificar los Valores Únicos: Revisa tu lista ordenada e identifica todos los valores distintos que aparecen. Estos valores únicos formarán la primera columna de tu tabla, usualmente llamada \(x_i\).
- Calcular la Frecuencia Absoluta (\(f_i\)): Para cada valor único \(x_i\), cuenta cuántas veces aparece en tu conjunto de datos total. Este conteo es la frecuencia absoluta. Coloca estos valores en la segunda columna. Al final, suma todas las frecuencias absolutas para obtener el total de datos \(N\). ¡Este es un buen punto de control para asegurarte de que no has omitido ningún dato!
- Calcular la Frecuencia Relativa (\(h_i\)): Ahora, crea una tercera columna. Para cada fila, divide la frecuencia absoluta (\(f_i\)) por el número total de datos (\(N\)). Es decir, calcula \(h_i = f_i / N\). Puedes dejarlo como decimal o multiplicarlo por 100 para obtener el porcentaje. La suma de esta columna debe dar 1 (o 100%).
- Calcular la Frecuencia Absoluta Acumulada (\(F_i\)): En la cuarta columna, vamos a acumular las frecuencias. El primer valor de \(F_i\) es igual al primer valor de \(f_i\). Para el segundo, suma el segundo \(f_i\) al primer \(F_i\). Continúa este proceso: cada \(F_i\) es la suma del \(f_i\) de su fila más el \(F_i\) de la fila anterior. El último valor de esta columna debe ser igual a \(N\).
- Calcular la Frecuencia Relativa Acumulada (\(H_i\)): Finalmente, en la quinta columna, divide cada valor de la frecuencia absoluta acumulada (\(F_i\)) entre el total de datos (\(N\)). O bien, puedes ir acumulando los valores de la frecuencia relativa (\(h_i\)). El último valor de esta columna debe ser 1 (o 100%).
¡Y listo! 🎉 Has construido tu primera tabla de frecuencias completa. Veamos cómo funciona esto en la práctica con un ejemplo detallado.
Ejemplo 1: Calificaciones de un Examen de Matemáticas
Un profesor ha recogido las calificaciones de sus 25 estudiantes en un examen reciente. Las calificaciones son las siguientes: 8, 7, 9, 10, 8, 6, 7, 8, 9, 10, 7, 8, 5, 6, 9, 8, 7, 7, 8, 9, 10, 6, 7, 8, 9. Construyamos la tabla de frecuencias para estos datos no agrupados.
Solución:
Paso 1: Ordenar los datos
Primero, ordenamos las 25 calificaciones de menor a mayor:
5, 6, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10
Paso 2: Identificar valores únicos (\(x_i\)) y calcular la Frecuencia Absoluta (\(f_i\))
Los valores únicos son las diferentes calificaciones obtenidas: 5, 6, 7, 8, 9, 10. Ahora contamos cuántas veces aparece cada una:
- Calificación 5: 1 vez
- Calificación 6: 3 veces
- Calificación 7: 6 veces
- Calificación 8: 7 veces
- Calificación 9: 5 veces
- Calificación 10: 3 veces
Sumamos las frecuencias: \(1 + 3 + 6 + 7 + 5 + 3 = 25\). Coincide con el número total de estudiantes (\(N=25\)), ¡así que vamos bien!
Paso 3 y 4: Calcular Frecuencias Relativas (\(h_i\)) y Acumuladas (\(F_i, H_i\))
Ahora, con esta información, podemos empezar a construir la tabla y calcular el resto de las columnas.
Así se ve la tabla de frecuencias completa:
| Calificación (\(x_i\)) | Frecuencia Absoluta (\(f_i\)) | Frecuencia Relativa (\(h_i\)) | Frecuencia Absoluta Acumulada (\(F_i\)) | Frecuencia Relativa Acumulada (\(H_i\)) |
|---|---|---|---|---|
| 5 | 1 | \(1/25 = 0.04\) | 1 | \(1/25 = 0.04\) |
| 6 | 3 | \(3/25 = 0.12\) | \(1+3=4\) | \(4/25 = 0.16\) |
| 7 | 6 | \(6/25 = 0.24\) | \(4+6=10\) | \(10/25 = 0.40\) |
| 8 | 7 | \(7/25 = 0.28\) | \(10+7=17\) | \(17/25 = 0.68\) |
| 9 | 5 | \(5/25 = 0.20\) | \(17+5=22\) | \(22/25 = 0.88\) |
| 10 | 3 | \(3/25 = 0.12\) | \(22+3=25\) | \(25/25 = 1.00\) |
| Total | \(N=25\) | \(1.00\) |
¡Ahí la tienes! Una tabla de frecuencias perfectamente construida que resume toda la información de las calificaciones.
Interpretando la Magia: ¿Qué nos dice la Tabla de Frecuencias?
Crear la tabla es solo la mitad del trabajo. La verdadera habilidad está en interpretarla. ¿Qué historias nos cuentan estos números organizados? 🧐
- La moda es evidente: Simplemente mirando la columna de frecuencia absoluta (\(f_i\)), podemos identificar la moda, que es el valor que más se repite. En nuestro ejemplo, la calificación que más se repite es el 8, con una frecuencia de 7.
- Concentración de datos: La columna de frecuencia relativa (\(h_i\)) nos muestra dónde se concentran los datos. Vemos que el 28% de los estudiantes obtuvieron un 8, y el 24% obtuvo un 7. ¡Más de la mitad de la clase (52%) tiene una calificación de 7 u 8!
- Análisis acumulativo: Las columnas acumuladas son muy potentes. Por ejemplo, si miramos la fila de la calificación 7 en la columna de Frecuencia Absoluta Acumulada (\(F_i\)), vemos el valor 10. Esto significa que 10 estudiantes obtuvieron una calificación de 7 o menos.
- Percentiles a la vista: La Frecuencia Relativa Acumulada (\(H_i\)) nos habla de porcentajes. En la fila del 9, el valor de \(H_i\) es 0.88. Esto nos dice que el 88% de los estudiantes obtuvieron una calificación de 9 o inferior. Esto también implica que solo el 12% de los estudiantes obtuvieron una calificación de 10.
Como puedes ver, una simple tabla transforma una lista desordenada de 25 números en información valiosa y fácil de digerir sobre el rendimiento del grupo.
Ejemplo 2: Número de Mascotas por Hogar
Se realiza una encuesta en un vecindario a 20 hogares para saber cuántas mascotas tienen. Los resultados son: 1, 2, 0, 3, 1, 1, 2, 0, 0, 1, 2, 4, 1, 1, 0, 2, 3, 1, 2, 0. Vamos a organizar estos datos.
Solución:
Paso 1: Ordenar los datos
0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 4
¡Un momento! Al contar, me doy cuenta de que son 19 datos, no 20. Reviso la lista original: 1, 2, 0, 3, 1, 1, 2, 0, 0, 1, 2, 4, 1, 1, 0, 2, 3, 1, 2, 0. Efectivamente, son 20. Volvamos a ordenar con cuidado.
0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 4, (Falta un '1' y un '2', hay un '0' de más). ¡Este es un error común! La atención al detalle es clave. Corrijamos el orden.
La lista original tiene:
Cinco '0's.
Siete '1's.
Cinco '2's.
Dos '3's.
Un '4'.
Total: 5+7+5+2+1=20. ¡Ahora sí! \(N=20\).
Datos ordenados: 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 4.
Paso 2: Construir la tabla
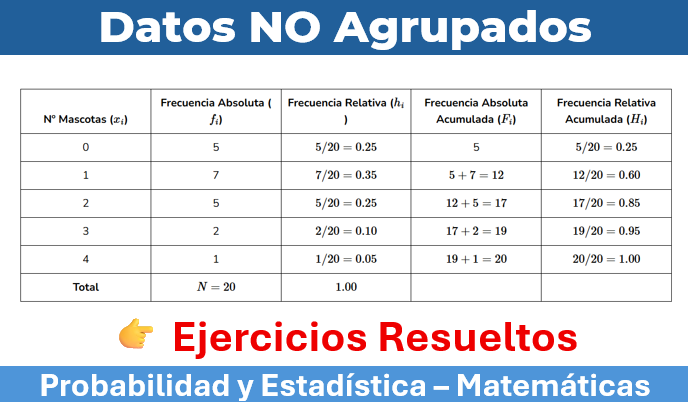
| Nº Mascotas (\(x_i\)) | Frecuencia Absoluta (\(f_i\)) | Frecuencia Relativa (\(h_i\)) | Frecuencia Absoluta Acumulada (\(F_i\)) | Frecuencia Relativa Acumulada (\(H_i\)) |
|---|---|---|---|---|
| 0 | 5 | \(5/20 = 0.25\) | 5 | \(5/20 = 0.25\) |
| 1 | 7 | \(7/20 = 0.35\) | \(5+7=12\) | \(12/20 = 0.60\) |
| 2 | 5 | \(5/20 = 0.25\) | \(12+5=17\) | \(17/20 = 0.85\) |
| 3 | 2 | \(2/20 = 0.10\) | \(17+2=19\) | \(19/20 = 0.95\) |
| 4 | 1 | \(1/20 = 0.05\) | \(19+1=20\) | \(20/20 = 1.00\) |
| Total | \(N=20\) | \(1.00\) |
Interpretación rápida:
- El número más común de mascotas es 1 (la moda), ya que 7 hogares tienen una mascota.
- El 25% de los hogares no tienen ninguna mascota.
- El 60% de los hogares tienen 1 mascota o ninguna.
- El 95% de los hogares tienen 3 mascotas o menos. Solo un 5% tiene 4 mascotas.
Ejemplo 3: Horas de Estudio Semanales
Se le preguntó a un grupo de 20 estudiantes de bachillerato cuántas horas dedican al estudio por semana. Las respuestas fueron las siguientes: 10, 12, 15, 12, 10, 11, 14, 13, 12, 11, 10, 15, 14, 12, 13, 12, 11, 10, 14, 13. Organiza estos datos en una tabla de frecuencias completa.
Solución:
Paso 1: Ordenar los datos
Comenzamos ordenando el conjunto de 20 datos de menor a mayor para facilitar el conteo:
10, 10, 10, 10, 11, 11, 11, 12, 12, 12, 12, 12, 13, 13, 13, 14, 14, 14, 15, 15
Paso 2: Identificar valores únicos (\(x_i\)) y Frecuencias Absolutas (\(f_i\))
Observamos los valores distintos y contamos cuántas veces aparece cada uno. El total de datos es \(N=20\).
- Horas de estudio 10: 4 veces
- Horas de estudio 11: 3 veces
- Horas de estudio 12: 5 veces
- Horas de estudio 13: 3 veces
- Horas de estudio 14: 3 veces
- Horas de estudio 15: 2 veces
La suma de las frecuencias es \(4 + 3 + 5 + 3 + 3 + 2 = 20\), lo cual confirma que hemos contado todos los datos.
Paso 3: Construcción de la tabla completa
Ahora procedemos a calcular las frecuencias relativas y acumuladas para completar nuestra tabla.
| Horas (\(x_i\)) | Frecuencia Absoluta (\(f_i\)) | Frecuencia Relativa (\(h_i\)) | Frecuencia Absoluta Acumulada (\(F_i\)) | Frecuencia Relativa Acumulada (\(H_i\)) |
|---|---|---|---|---|
| 10 | 4 | \(4/20 = 0.20\) | 4 | \(4/20 = 0.20\) |
| 11 | 3 | \(3/20 = 0.15\) | \(4+3=7\) | \(7/20 = 0.35\) |
| 12 | 5 | \(5/20 = 0.25\) | \(7+5=12\) | \(12/20 = 0.60\) |
| 13 | 3 | \(3/20 = 0.15\) | \(12+3=15\) | \(15/20 = 0.75\) |
| 14 | 3 | \(3/20 = 0.15\) | \(15+3=18\) | \(18/20 = 0.90\) |
| 15 | 2 | \(2/20 = 0.10\) | \(18+2=20\) | \(20/20 = 1.00\) |
| Total | \(N=20\) | \(1.00\) |
Análisis rápido: La tabla nos muestra que la cantidad de horas de estudio más frecuente (la moda) es de 12 horas semanales, ya que 5 estudiantes (un 25% del grupo) reportaron esta cifra. También podemos ver que 12 estudiantes, es decir, el 60% del grupo, estudian 12 horas o menos por semana.
Ejemplo 4: Número de Artículos Publicados
Se encuesta a 24 investigadores de una universidad sobre el número de artículos científicos que han publicado en el último año. Los datos son: 2, 1, 0, 3, 1, 1, 2, 4, 0, 1, 2, 1, 0, 0, 1, 2, 3, 1, 2, 0, 1, 4, 2, 1. Elabora la tabla de frecuencias para este conjunto de datos.
Solución:
Paso 1: Ordenar los datos
Organizamos los 24 datos en orden ascendente:
0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4
Paso 2: Identificar valores únicos (\(x_i\)) y Frecuencias Absolutas (\(f_i\))
Contamos las repeticiones de cada valor. El número total de datos es \(N=24\).
- 0 artículos: 5 veces
- 1 artículo: 9 veces
- 2 artículos: 6 veces
- 3 artículos: 2 veces
- 4 artículos: 2 veces
Verificamos la suma: \(5 + 9 + 6 + 2 + 2 = 24\). ¡Correcto!
Paso 3: Construcción de la tabla completa
Con los conteos listos, calculamos las demás columnas de la tabla.
| Nº Artículos (\(x_i\)) | Frecuencia Absoluta (\(f_i\)) | Frecuencia Relativa (\(h_i\)) | Frecuencia Absoluta Acumulada (\(F_i\)) | Frecuencia Relativa Acumulada (\(H_i\)) |
|---|---|---|---|---|
| 0 | 5 | \(5/24 \approx 0.208\) | 5 | \(5/24 \approx 0.208\) |
| 1 | 9 | \(9/24 = 0.375\) | \(5+9=14\) | \(14/24 \approx 0.583\) |
| 2 | 6 | \(6/24 = 0.250\) | \(14+6=20\) | \(20/24 \approx 0.833\) |
| 3 | 2 | \(2/24 \approx 0.083\) | \(20+2=22\) | \(22/24 \approx 0.917\) |
| 4 | 2 | \(2/24 \approx 0.083\) | \(22+2=24\) | \(24/24 = 1.000\) |
| Total | \(N=24\) | \(1.000\) |
Análisis rápido: De esta tabla podemos deducir que lo más común es que un investigador publique 1 artículo al año (la moda), con un 37.5% de los encuestados en esa categoría. Además, un 58.3% de los investigadores publicaron 1 artículo o menos. Solo una pequeña fracción, aproximadamente el 16.6% (los que publicaron 3 o 4 artículos), son los más productivos.
Conclusión: Tu Primer Gran Paso en el Análisis de Datos
Aprender sobre datos no agrupados, ayudan mucho si en algún momento de la vida te inclinas por estudiar análisis de datos que hoy en día es una carrera muy demandada. Con este artículo espero hayas podido construir e interpretar una de las herramientas más fundamentales en estadística. Las tablas de frecuencias para datos no agrupados son la base para organizar datos, visualizar distribuciones y preparar el terreno para análisis más complejos como el cálculo de la media, la mediana, la desviación estándar y la creación de gráficos (como diagramas de barras o histogramas).
Dominar esta técnica te da el poder de transformar listas de números sin sentido en una fuente clara de conocimiento. La próxima vez que te enfrentes a un conjunto de datos, ya no verás un caos, sino una oportunidad para descubrir la historia que esconden. ¡Sigue practicando y estarás en camino de convertirte en un experto analista de datos! 💪
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar