¿Te pierdes con el $\Delta x$ y el álgebra infinita?
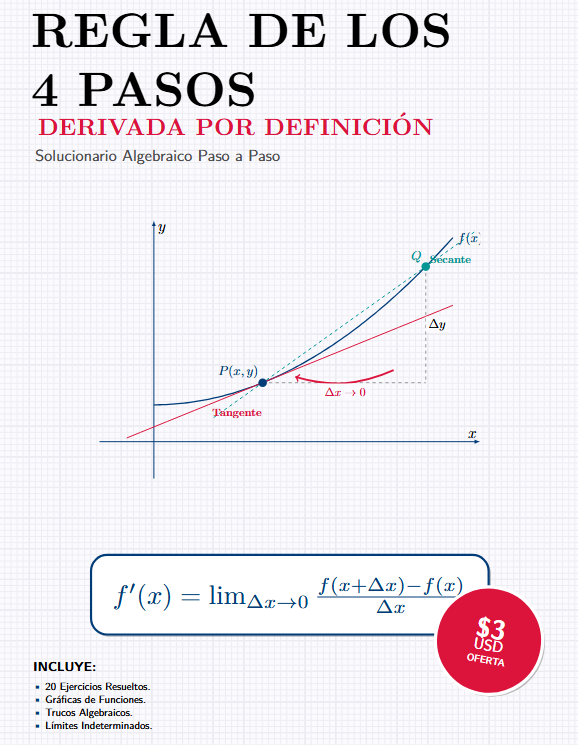
La "Regla de los 4 Pasos" es el filtro número uno en los exámenes de Cálculo. No es que no sepas derivar, es que el álgebra para eliminar la indeterminación ($0/0$) suele ser complicada.
Este solucionario es tu "guía de supervivencia" algebraica:
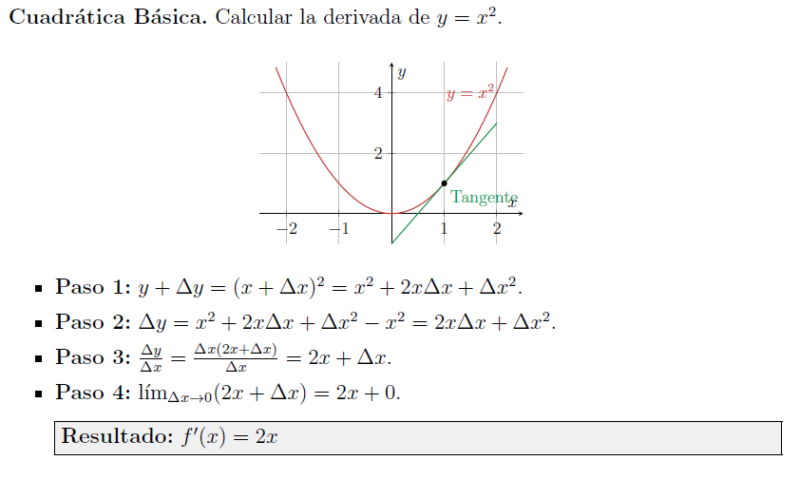
📈 20 Problemas Desglosados: Te mostramos cómo desarrollar binomios, racionalizar raíces (conjugados) y simplificar fracciones complejas paso a paso.
📐 Gráficas de Funciones: Hemos añadido gráficas precisas (Lineales, Cuadráticas, Hipérbolas) para que entiendas geométricamente qué es lo que estás calculando (la pendiente de la tangente).
🧠 Trucos Algebraicos: Aprende a cancelar los términos correctos para que el límite salga directo.
Nivel Progresivo: Empieza con $y=x^2$ y termina dominando $y=\sqrt{x+2}$ o $y=1/(x+1)$.
Si dominas la definición, las fórmulas directas serán pan comido después.

Valoraciones
No hay valoraciones aún.