Máximo Común Divisor y Mínimo Común Múltiplo - Ejercicios Resueltos
¡Hola amigos de Fisimat, Bienvenidos! En el vasto universo de las matemáticas, existen conceptos fundamentales que actúan como pilares para la comprensión de operaciones más complejas. Entre ellos, el Máximo Común Divisor (MCD) y el Mínimo Común Múltiplo (mcm) destacan por su recurrencia y su vital importancia en diversas áreas. Aunque a primera vista puedan parecer simples operaciones numéricas, su correcta aplicación es crucial para resolver problemas cotidianos y avanzar en el estudio de la aritmética, el álgebra y áreas significativas como la física.
Este artículo te guiará a través de la definición, cálculo y aplicación de estos dos conceptos. Desde la simplificación de fracciones hasta la planificación de eventos con ciclos repetitivos, el MCD y el mcm son herramientas poderosas que facilitan la resolución de una amplia gama de situaciones. Comprenderlos no solo te ayudará a mejorar tus habilidades matemáticas, sino que también te proporcionará una base sólida para temas más avanzados como el álgebra y la teoría de números. 🤓
✅ Es importante leer sobre Factores Primos
[alert-warning] 🔎 Queríamos hacer dos artículos por separado para explicar mejor el tema de MCD y mcm sin embargo, decidimos unir ambos temas pero explicando a detalle cada situación y combinar situaciones que son más comunes en matemáticas [/alert-warning]
El Máximo Común Divisor y el Mínimo Común Múltiplo
El Máximo Común Divisor (MCD) y el Mínimo Común Múltiplo (mcm) son conceptos que involucran las relaciones entre números enteros. Para entenderlos a fondo, primero debemos repasar qué son los divisores y los múltiplos de un número.
Divisores y Múltiplos
Divisor de un número: Un divisor de un número entero $N$ es cualquier número entero que divide a $N$ de manera exacta, es decir, el resto de la división es cero.
- Ejemplo: Los divisores de 12 son 1, 2, 3, 4, 6 y 12, ya que:
- $12 \div 1 = 12$
- $12 \div 2 = 6$
- $12 \div 3 = 4$
- $12 \div 4 = 3$
- $12 \div 6 = 2$
- $12 \div 12 = 1$
Múltiplo de un número: Un múltiplo de un número entero $N$ es el resultado de multiplicar $N$ por cualquier otro número entero. Los múltiplos de un número son infinitos.
- Ejemplo: Los primeros múltiplos de 5 son 5, 10, 15, 20, 25, ... (resultados de $5 \times 1, 5 \times 2, 5 \times 3$, etc.)
Máximo Común Divisor (MCD)
El Máximo Común Divisor (MCD) de dos o más números enteros es el mayor número entero que los divide a todos exactamente. Se denota como $\text{MCD}(a, b)$ o $\text{MCD}(a, b, c, ...)$.
Veamos un ejemplo gráfico
Paso 1: Descomponer en factores primos
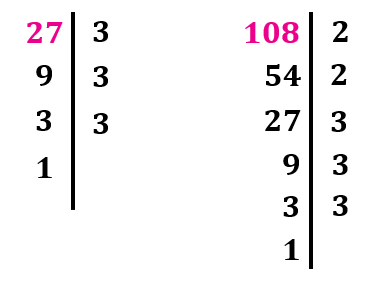
Paso 2: Identificamos los factores comunes

Paso 3: Multiplicamos los factores
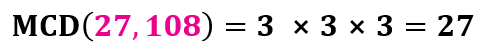
Métodos para calcular el MCD:
- Método por listado de divisores:
- Listar todos los divisores de cada número.
- Identificar los divisores comunes a todos los números.
- El mayor de esos divisores comunes es el MCD.
- Ejemplo: Calcular el MCD de 12 y 18.
- Divisores de 12: {1, 2, 3, 4, 6, 12}
- Divisores de 18: {1, 2, 3, 6, 9, 18}
- Divisores comunes: {1, 2, 3, 6}
- El mayor divisor común es 6. Por lo tanto, $\text{MCD}(12, 18) = 6$.
- Método por descomposición en factores primos: Este es el método más eficiente para números grandes.
- Descomponer cada número en sus factores primos.
- Identificar los factores primos comunes a todas las descomposiciones.
- Multiplicar estos factores primos comunes, elevados a su menor exponente.
- Ejemplo: Calcular el MCD de 36 y 48.
- Descomposición de 36:
$$36 = 2^2 \times 3^2$$ - Descomposición de 48:
$$48 = 2^4 \times 3^1$$ - Factores primos comunes: 2 y 3.
- Menor exponente para 2 es 2 ($2^2$). Menor exponente para 3 es 1 ($3^1$).
- $\text{MCD}(36, 48) = 2^2 \times 3^1 = 4 \times 3 = 12$.
- Descomposición de 36:
Mínimo Común Múltiplo (mcm)
El Mínimo Común Múltiplo (mcm) de dos o más números enteros es el menor número entero positivo que es múltiplo de todos ellos. Se denota como $\text{mcm}(a, b)$ o $\text{mcm}(a, b, c, ...)$.
Veamos un ejemplo gráfico.
Paso 1: Descomponer cada uno de los números en sus factores primos.
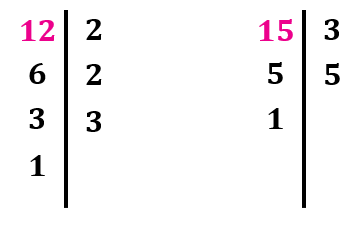
Paso 2: Después tomamos los factores comunes y no comunes, el mayor número de veces que se repitan y los multiplicamos.
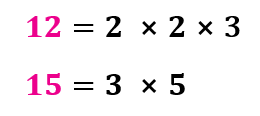
Paso 3. El resultado es el mcm de los números 12 y 15.
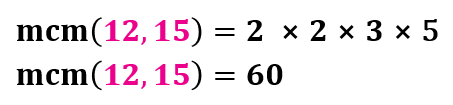
Métodos para calcular el mcm:
- Método por listado de múltiplos:
- Listar los primeros múltiplos de cada número.
- Identificar los múltiplos comunes a todos los números.
- El menor de esos múltiplos comunes (distinto de cero) es el mcm.
- Ejemplo: Calcular el mcm de 4 y 6.
- Múltiplos de 4: {4, 8, 12, 16, 20, 24, ...}
- Múltiplos de 6: {6, 12, 18, 24, 30, ...}
- Múltiplos comunes: {12, 24, ...}
- El menor múltiplo común es 12. Por lo tanto, $\text{mcm}(4, 6) = 12$.
- Método por descomposición en factores primos: Este es el método más eficiente para números grandes.
- Descomponer cada número en sus factores primos.
- Identificar todos los factores primos (comunes y no comunes) presentes en las descomposiciones.
- Multiplicar estos factores primos, elevados a su mayor exponente.
- Ejemplo: Calcular el mcm de 36 y 48.
- Descomposición de 36:
$$36 = 2^2 \times 3^2$$ - Descomposición de 48:
$$48 = 2^4 \times 3^1$$ - Factores primos presentes: 2 y 3.
- Mayor exponente para 2 es 4 ($2^4$). Mayor exponente para 3 es 2 ($3^2$).
- $\text{mcm}(36, 48) = 2^4 \times 3^2 = 16 \times 9 = 144$.
- Descomposición de 36:
🤓 Relación entre MCD y mcm
Existe una relación importante entre el MCD y el mcm de dos números enteros $a$ y $b$:
$$\text{MCD}(a, b) \times \text{mcm}(a, b) = a \times b$$
Esta propiedad es muy útil para calcular uno si ya conocemos el otro y los números originales. 👇
- Ejemplo: Sabemos que $\text{MCD}(36, 48) = 12$ y $\text{mcm}(36, 48) = 144$.
- $12 \times 144 = 1728$
- $36 \times 48 = 1728$
- Se cumple la relación.
Ejercicios Resueltos para Practicar
A continuación, se presentan ejercicios de dificultad creciente para practicar el cálculo del MCD y el mcm.
Solución:
Para calcular el MCD de 20 y 30, usaremos el método de listado de divisores, ya que son números pequeños.
▷ Paso 1: Listar los divisores de 20.
Los divisores de 20 son los números que dividen a 20 de forma exacta.
Divisores de 20: {1, 2, 4, 5, 10, 20}
▷ Paso 2: Listar los divisores de 30.
Los divisores de 30 son los números que dividen a 30 de forma exacta.
Divisores de 30: {1, 2, 3, 5, 6, 10, 15, 30}
▷ Paso 3: Identificar los divisores comunes a ambos números.
Divisores comunes de 20 y 30: {1, 2, 5, 10}
▷ Paso 4: El mayor de los divisores comunes es el MCD.
El mayor número en el conjunto de divisores comunes es 10.
Por lo tanto, $\text{MCD}(20, 30) = 10$.
Solución:
Para encontrar el mcm de 8 y 12, usaremos el método de listado de múltiplos.
▷ Paso 1: Listar los primeros múltiplos de 8.
Múltiplos de 8: {8, 16, 24, 32, 40, 48, ...}
▷ Paso 2: Listar los primeros múltiplos de 12.
Múltiplos de 12: {12, 24, 36, 48, 60, ...}
▷ Paso 3: Identificar los múltiplos comunes.
Los múltiplos comunes que aparecen en ambas listas son 24, 48, etc.
▷ Paso 4: El menor de los múltiplos comunes (distinto de cero) es el mcm.
El menor múltiplo común es 24.
Por lo tanto, $\text{mcm}(8, 12) = 24$.
Solución
Usaremos el método de descomposición en factores primos para calcular el MCD.
▷ Paso 1: Descomponer 72 en factores primos.
$$72 = 2 \times 36$$
$$36 = 2 \times 18$$
$$18 = 2 \times 9$$
$$9 = 3 \times 3$$
Entonces, $72 = 2 \times 2 \times 2 \times 3 \times 3 = 2^3 \times 3^2$.
▷ Paso 2: Descomponer 108 en factores primos.
$$108 = 2 \times 54$$
$$54 = 2 \times 27$$
$$27 = 3 \times 9$$
$$9 = 3 \times 3$$
Entonces, $108 = 2 \times 2 \times 3 \times 3 \times 3 = 2^2 \times 3^3$.
▷ Paso 3: Identificar los factores primos comunes y tomar el menor exponente.
Factores primos comunes son 2 y 3.
Para el factor 2: El menor exponente es 2 (de $2^2$).
Para el factor 3: El menor exponente es 2 (de $3^2$).
▷ Paso 4: Multiplicar los factores comunes con sus menores exponentes.
$\text{MCD}(72, 108) = 2^2 \times 3^2 = 4 \times 9 = 36$.
Solución:
Utilizaremos la descomposición en factores primos para determinar el mcm.
▷ Paso 1: Descomponer 75 en factores primos.
$$75 = 3 \times 25$$
$$25 = 5 \times 5$$
Entonces, $75 = 3^1 \times 5^2$.
▷ Paso 2: Descomponer 90 en factores primos.
$$90 = 2 \times 45$$
$$45 = 3 \times 15$$
$$15 = 3 \times 5$$
Entonces, $90 = 2^1 \times 3^2 \times 5^1$.
▷ Paso 3: Identificar todos los factores primos (comunes y no comunes) y tomar el mayor exponente.
Factores primos presentes son 2, 3 y 5.
Para el factor 2: El mayor exponente es 1 (de $2^1$).
Para el factor 3: El mayor exponente es 2 (de $3^2$).
Para el factor 5: El mayor exponente es 2 (de $5^2$).
▷ Paso 4: Multiplicar todos los factores primos con sus mayores exponentes.
$\text{mcm}(75, 90) = 2^1 \times 3^2 \times 5^2 = 2 \times 9 \times 25 = 18 \times 25 = 450$.
Solución
Para ambos cálculos, utilizaremos la descomposición en factores primos.
▷ Paso 1: Descomponer cada número en factores primos.
Para 60: $60 = 2^2 \times 3^1 \times 5^1$
Para 90: $90 = 2^1 \times 3^2 \times 5^1$
Para 120: $120 = 2^3 \times 3^1 \times 5^1$
Cálculo del MCD:
▷ Paso 2 (MCD): Identificar factores comunes con el menor exponente.
Factor 2: El menor exponente es 1 ($2^1$).
Factor 3: El menor exponente es 1 ($3^1$).
Factor 5: El menor exponente es 1 ($5^1$).
$\text{MCD}(60, 90, 120) = 2^1 \times 3^1 \times 5^1 = 2 \times 3 \times 5 = 30$.
Cálculo del mcm:
▷ Paso 2 (mcm): Identificar todos los factores (comunes y no comunes) con el mayor exponente.
Factor 2: El mayor exponente es 3 ($2^3$).
Factor 3: El mayor exponente es 2 ($3^2$).
Factor 5: El mayor exponente es 1 ($5^1$).
$\text{mcm}(60, 90, 120) = 2^3 \times 3^2 \times 5^1 = 8 \times 9 \times 5 = 72 \times 5 = 360$.
Solución:
Este problema implica encontrar el mayor número de "grupos iguales" (cestas) que se pueden formar a partir de dos cantidades. Esto es una aplicación directa del Máximo Común Divisor.
▷ Paso 1: Identificar qué se debe calcular.
Necesitamos el MCD de 48 y 72.
▷ Paso 2: Descomponer 48 en factores primos.
$$48 = 2^4 \times 3^1$$
▷ Paso 3: Descomponer 72 en factores primos.
$$72 = 2^3 \times 3^2$$
▷ Paso 4: Calcular el MCD de 48 y 72.
Factores comunes: 2 y 3.
Menor exponente para 2 es 3 ($2^3$).
Menor exponente para 3 es 1 ($3^1$).
$\text{MCD}(48, 72) = 2^3 \times 3^1 = 8 \times 3 = 24$.
▷ Paso 5: Interpretar el resultado.
El MCD, 24, representa el mayor número de cestas iguales que se pueden hacer.
▷ Paso 6: Calcular el contenido de cada cesta.
Número de manzanas por cesta: $48 \div 24 = 2$ manzanas.
Número de peras por cesta: $72 \div 24 = 3$ peras.
Respuesta: Se pueden hacer 24 cestas. Cada cesta contendrá 2 manzanas y 3 peras.
Solución
Este problema implica encontrar cuándo dos eventos que se repiten en ciclos diferentes coincidirán por primera vez. Esto es una aplicación directa del Mínimo Común Múltiplo.
▷ Paso 1: Identificar qué se debe calcular.
Necesitamos el mcm de 30 y 45.
▷ Paso 2: Descomponer 30 en factores primos.
$$30 = 2^1 \times 3^1 \times 5^1$$
▷ Paso 3: Descomponer 45 en factores primos.
$$45 = 3^2 \times 5^1$$
▷ Paso 4: Calcular el mcm de 30 y 45.
Factores presentes: 2, 3 y 5.
Mayor exponente para 2 es 1 ($2^1$).
Mayor exponente para 3 es 2 ($3^2$).
Mayor exponente para 5 es 1 ($5^1$).
$\text{mcm}(30, 45) = 2^1 \times 3^2 \times 5^1 = 2 \times 9 \times 5 = 18 \times 5 = 90$.
▷ Paso 5: Interpretar el resultado.
El mcm, 90, significa que coincidirán cada 90 minutos.
▷ Paso 6: Calcular la hora de la próxima coincidencia.
Si partieron a las 8:00 AM y coinciden en 90 minutos, 90 minutos equivalen a 1 hora y 30 minutos.
Hora de partida: 8:00 AM
Tiempo transcurrido: 1 hora y 30 minutos
Hora de coincidencia: 8:00 AM + 1 hora 30 minutos = 9:30 AM.
Respuesta: Volverán a coincidir en la estación a las 9:30 AM.
Solución
Este problema requiere encontrar la mayor longitud común en la que se pueden dividir tres cantidades. Esto es una aplicación del Máximo Común Divisor para tres números.
▷ Paso 1: Identificar qué se debe calcular.
Necesitamos el MCD de 105, 140 y 175.
▷ Paso 2: Descomponer cada número en factores primos.
Para 105:
$$105 = 3 \times 35$$
$$35 = 5 \times 7$$
$$105 = 3^1 \times 5^1 \times 7^1$$
Para 140:
$$140 = 2 \times 70$$
$$70 = 2 \times 35$$
$$35 = 5 \times 7$$
$$140 = 2^2 \times 5^1 \times 7^1$$
Para 175:
$$175 = 5 \times 35$$
$$35 = 5 \times 7$$
$$175 = 5^2 \times 7^1$$
▷ Paso 3: Calcular el MCD de 105, 140 y 175.
Identificar factores primos comunes y tomar el menor exponente.
Factores comunes: 5 y 7.
Para el factor 5: El menor exponente es 1 (de $5^1$).
Para el factor 7: El menor exponente es 1 (de $7^1$).
$\text{MCD}(105, 140, 175) = 5^1 \times 7^1 = 5 \times 7 = 35$.
Respuesta: Cada trozo de tela debe medir 35 cm.
Solución
Similar al problema de los autobuses, este problema busca el momento en que tres eventos cíclicos coinciden por primera vez. Esto es una aplicación del Mínimo Común Múltiplo para tres números.
▷ Paso 1: Identificar qué se debe calcular.
Necesitamos el mcm de 15, 20 y 25.
▷ Paso 2: Descomponer cada número en factores primos.
Para 15: $15 = 3^1 \times 5^1$
Para 20: $20 = 2^2 \times 5^1$
Para 25: $25 = 5^2$
▷ Paso 3: Calcular el mcm de 15, 20 y 25.
Identificar todos los factores primos (comunes y no comunes) y tomar el mayor exponente.
Factores presentes: 2, 3 y 5.
Mayor exponente para 2 es 2 ($2^2$).
Mayor exponente para 3 es 1 ($3^1$).
Mayor exponente para 5 es 2 ($5^2$).
$\text{mcm}(15, 20, 25) = 2^2 \times 3^1 \times 5^2 = 4 \times 3 \times 25 = 12 \times 25 = 300$.
Paso 4: Interpretar el resultado.
El mcm, 300, significa que volverán a sonar juntos cada 300 minutos.
▷ Paso 5: Convertir los minutos a horas y minutos y calcular la hora final.
300 minutos $\div$ 60 minutos/hora = 5 horas.
Si sonaron juntos a las 7:00 AM, volverán a sonar 5 horas después.
7:00 AM + 5 horas = 12:00 PM (mediodía).
Respuesta: Los tres relojes volverán a sonar juntos a las 12:00 PM.
Conclusión
El Máximo Común Divisor y el Mínimo Común Múltiplo son más que simples operaciones matemáticas; son herramientas esenciales que nos permiten entender y resolver problemas relacionados con la divisibilidad y la concurrencia de eventos. Desde la distribución equitativa de objetos hasta la sincronización de ciclos, su dominio proporciona una base sólida para la aritmética y disciplinas más avanzadas.
Al comprender cómo calcular el MCD y el mcm, ya sea mediante la enumeración de divisores/múltiplos o la eficiente descomposición en factores primos, equipas tu mente con habilidades analíticas fundamentales. Estos conceptos, aparentemente sencillos, son la puerta de entrada a la comprensión de propiedades numéricas más profundas y a la aplicación de las matemáticas en situaciones prácticas de la vida y en el desarrollo de la ingeniería y la robótica.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar