Comparación de Fracciones - Ejercicios Resueltos
¡Bienvenidos amigos de Fisimat!, hoy hablaremos sobre un tema nuevo, en el aprendizaje de las fracciones, comprender cómo representarlas de la manera más sencilla y cómo determinar cuál es mayor o menor es tan crucial como dominar sus operaciones básicas. La simplificación de fracciones nos permite expresar una misma cantidad utilizando los números más pequeños posibles, lo que facilita tanto la lectura como el cálculo. Por otro lado, la comparación de fracciones es una habilidad esencial que nos ayuda a ordenar cantidades fraccionarias y tomar decisiones informadas, ya sea para saber quién comió más pizza o para ajustar medidas en un proyecto de ingeniería. ¿cómo ves? 😃
Este artículo o post de aritmética te guiará a través de las técnicas para simplificar fracciones a su mínima expresión y los métodos efectivos para compararlas, sin importar si tienen el mismo o diferente denominador. Dominar estas habilidades no solo te hará más eficiente en tus cálculos, sino que también te dará una comprensión más profunda del valor relativo de las cantidades fraccionarias. Prepárate para pulir tus conocimientos sobre fracciones y llevarlos al siguiente nivel.
Una vez que comprendemos qué son las fracciones y cómo operarlas, el siguiente paso lógico es aprender a trabajar con ellas de forma más eficiente y a determinar su valor relativo.
Simplificación de Fracciones (Reducción a su Mínima Expresión)
Simplificar una fracción significa transformarla en una fracción equivalente donde el numerador y el denominador son los números enteros más pequeños posibles. Esto se logra dividiendo tanto el numerador como el denominador por su Máximo Común Divisor (MCD). Una fracción está en su mínima expresión (o es irreducible) cuando su MCD de numerador y denominador es 1.
Método por Divisiones Sucesivas
Este método consiste en dividir el numerador y el denominador por divisores comunes (generalmente números primos como 2, 3, 5, etc.) hasta que ya no haya más divisores comunes aparte del 1.
[alert-note]
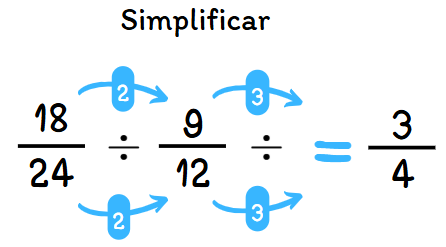
Ejemplo: Simplificar $\frac{18}{24}$.
[/alert-note]
Solución:
- Ambos son divisibles por 2: $\frac{18 \div 2}{24 \div 2} = \frac{9}{12}$
- Ahora, 9 y 12 son divisibles por 3: $\frac{9 \div 3}{12 \div 3} = \frac{3}{4}$
- La fracción $\frac{3}{4}$ ya no se puede simplificar más, porque el MCD de 3 y 4 es 1.
Método usando el Máximo Común Divisor (MCD)
Este método es más directo, especialmente para números grandes, ya que solo requiere una división.
- Calcula el MCD del numerador y el denominador.
- Divide tanto el numerador como el denominador por ese MCD.
[alert-note]
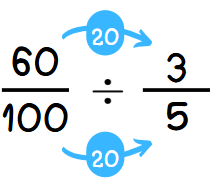
Ejemplo: Simplificar $\frac{60}{100}$.
[/alert-note]
Solución:
- Calcular el MCD de 60 y 100:
- Factores primos de 60: $60 = 2^2 \times 3^1 \times 5^1$
- Factores primos de 100: $100 = 2^2 \times 5^2$
- MCD(60, 100) = $2^2 \times 5^1 = 4 \times 5 = 20$
- Dividir numerador y denominador por el MCD:
$$\frac{60 \div 20}{100 \div 20} = \frac{3}{5}$$
- Calcular el MCD de 60 y 100:
Comparación de Fracciones
Comparar fracciones es determinar si una es mayor, menor o igual que otra. Existen varios métodos dependiendo de los denominadores.
Fracciones con el Mismo Denominador
Si dos o más fracciones tienen el mismo denominador, la fracción con el mayor numerador es la mayor.
[alert-note]
Ejemplo: Compara $\frac{5}{7}$ y $\frac{3}{7}$.
[/alert-note]
Solución:
Como $5 > 3$, entonces $\frac{5}{7} > \frac{3}{7}$.
Fracciones con el Mismo Numerador
Si dos o más fracciones tienen el mismo numerador, la fracción con el menor denominador es la mayor. Esto se debe a que, si se divide el mismo total en menos partes, cada parte es más grande.
[alert-note]
Ejemplo: Compara $\frac{1}{2}$ y $\frac{1}{4}$.
[/alert-note]
Solución:
Como $2 < 4$, entonces $\frac{1}{2} > \frac{1}{4}$.
Fracciones con Diferente Numerador y Denominador
Este es el caso más común y requiere un paso intermedio para hacer la comparación efectiva.
Método del Denominador Común (usando el mcm)
Este es el método más fiable y se basa en convertir las fracciones a fracciones equivalentes con un denominador común, preferiblemente el Mínimo Común Múltiplo (mcm) de los denominadores originales.
- Calcula el mcm de los denominadores.
- Convierte cada fracción a una fracción equivalente con ese mcm como denominador.
- Compara las nuevas fracciones (ahora con el mismo denominador) observando sus numeradores.
[alert-note]
Ejemplo: Compara $\frac{2}{3}$ y $\frac{3}{4}$.
[/alert-note]
Solución:
- mcm(3, 4) = 12
- Convertir:
$$\frac{2}{3} = \frac{2 \times 4}{3 \times 4} = \frac{8}{12}$$
$$\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}$$ - Comparar: Como $8 < 9$, entonces $\frac{8}{12} < \frac{9}{12}$.
Por lo tanto, $\frac{2}{3} < \frac{3}{4}$.
Método de Productos Cruzados
Este método es rápido para comparar dos fracciones sin necesidad de encontrar un denominador común, aunque no ayuda a visualizarlas.
- Multiplica el numerador de la primera fracción por el denominador de la segunda.
- Multiplica el numerador de la segunda fracción por el denominador de la primera.
- Compara los resultados de estas multiplicaciones:
- Si el primer producto es mayor que el segundo, la primera fracción es mayor.
- Si el primer producto es menor que el segundo, la primera fracción es menor.
- Si los productos son iguales, las fracciones son equivalentes.
[alert-note]
Ejemplo: Compara $\frac{2}{3}$ y $\frac{3}{4}$.
[/alert-note]
Solución:
- $2 \times 4 = 8$
- $3 \times 3 = 9$
- Comparar: Como $8 < 9$, entonces $\frac{2}{3} < \frac{3}{4}$.
Ejercicios Resueltos de Simplificación de Fracciones
Practica la simplificación y comparación de fracciones con estos ejercicios detallados.
Solución
Simplificaremos la fracción dividiendo el numerador y el denominador por su Máximo Común Divisor (MCD).
▷ Paso 1 Encontrar el MCD de 15 y 25.
Descomposición de 15: $15 = 3 \times 5$
Descomposición de 25: $25 = 5^2$
El único factor primo común es 5, y su menor exponente es 1 ($5^1$).
MCD(15, 25) = 5.
▷ Paso 2 Dividir el numerador y el denominador por el MCD.
$$\frac{15 \div 5}{25 \div 5} = \frac{3}{5}$$
La fracción en su mínima expresión es $\frac{3}{5}$.
Solución
Simplificaremos la fracción utilizando divisiones sucesivas.
▷ Paso 1 Dividir por un factor común (por ejemplo, 2).
Ambos son pares:
$$\frac{42 \div 2}{56 \div 2} = \frac{21}{28}$$
▷ Paso 2 Dividir por otro factor común (por ejemplo, 7).
Ambos son divisibles por 7:
$$\frac{21 \div 7}{28 \div 7} = \frac{3}{4}$$
▷ Paso 3 Verificar si se puede simplificar más.
El 3 y el 4 no tienen divisores comunes aparte del 1.
La fracción en su mínima expresión es $\frac{3}{4}$.
Solución
Las fracciones tienen el mismo denominador. En este caso, la fracción con el mayor numerador es la mayor.
▷ Paso 1 Comparar los numeradores.
Numerador de la primera fracción: 7
Numerador de la segunda fracción: 4
Como $7 > 4$.
▷ Paso 2 Establecer la relación.
Por lo tanto, $\frac{7}{9} > \frac{4}{9}$.
Solución
Las fracciones tienen el mismo numerador. En este caso, la fracción con el menor denominador es la mayor.
▷ Paso 1 Comparar los denominadores.
Denominador de la primera fracción: 6
Denominador de la segunda fracción: 8
Como $6 < 8$.
▷ Paso 2 Establecer la relación.
Por lo tanto, $\frac{5}{6} > \frac{5}{8}$.
Solución
Utilizaremos el Mínimo Común Múltiplo (mcm) para encontrar un denominador común.
▷ Paso 1 Encontrar el mcm de los denominadores (4 y 6).
Descomposición de 4: $4 = 2^2$
Descomposición de 6: $6 = 2 \times 3$
mcm(4, 6) = $2^2 \times 3 = 4 \times 3 = 12$.
▷ Paso 2 Convertir cada fracción a una equivalente con denominador 12.
Para $\frac{3}{4}$:
$$ \frac{3 \times (12 \div 4)}{4 \times (12 \div 4)} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12} $$
Para $\frac{5}{6}$:
$$ \frac{5 \times (12 \div 6)}{6 \times (12 \div 6)} = \frac{5 \times 2}{6 \times 2} = \frac{10}{12} $$
▷ Paso 3 Comparar las nuevas fracciones.
Comparamos $\frac{9}{12}$ y $\frac{10}{12}$.
Como $9 < 10$, entonces $\frac{9}{12} < \frac{10}{12}$.
Por lo tanto, $\frac{3}{4} < \frac{5}{6}$.
Solución
Utilizaremos el método de productos cruzados para comparar las fracciones.
▷ Paso 1 Multiplicar el numerador de la primera fracción por el denominador de la segunda.
$$7 \times 7 = 49$$
▷ Paso 2 Multiplicar el numerador de la segunda fracción por el denominador de la primera.
$$5 \times 8 = 40$$
▷ Paso 3 Comparar los resultados.
Como $49 > 40$.
▷ Paso 4 Establecer la relación.
La primera fracción es mayor.
Por lo tanto, $\frac{7}{8} > \frac{5}{7}$.
Solución
Para ordenar fracciones, necesitamos convertirlas a un denominador común.
▷ Paso 1 Encontrar el mcm de los denominadores (2, 3, 4).
Descomposición de 2: $2 = 2^1$
Descomposición de 3: $3 = 3^1$
Descomposición de 4: $4 = 2^2$
mcm(2, 3, 4) = $2^2 \times 3 = 4 \times 3 = 12$.
▷ Paso 2 Convertir cada fracción a una equivalente con denominador 12.
Para $\frac{1}{2}$:
$$ \frac{1 \times (12 \div 2)}{2 \times (12 \div 2)} = \frac{1 \times 6}{2 \times 6} = \frac{6}{12} $$
Para $\frac{2}{3}$:
$$ \frac{2 \times (12 \div 3)}{3 \times (12 \div 3)} = \frac{2 \times 4}{3 \times 4} = \frac{8}{12} $$
Para $\frac{3}{4}$:
$$ \frac{3 \times (12 \div 4)}{4 \times (12 \div 4)} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12} $$
▷ Paso 3 Ordenar las fracciones equivalentes por sus numeradores.
Las fracciones equivalentes son $\frac{6}{12}, \frac{8}{12}, \frac{9}{12}$.
Ordenadas: $\frac{6}{12} < \frac{8}{12} < \frac{9}{12}$.
▷ Paso 4 Escribir el orden con las fracciones originales.
Por lo tanto, $\frac{1}{2} < \frac{2}{3} < \frac{3}{4}$.
Solución
Podemos verificar la equivalencia de varias maneras: simplificando la primera fracción o usando productos cruzados. Usaremos la simplificación.
▷ Paso 1 Simplificar la primera fracción $\frac{16}{20}$.
El MCD de 16 y 20 es 4.
$$\frac{16 \div 4}{20 \div 4} = \frac{4}{5}$$
▷ Paso 2 Comparar la fracción simplificada con la segunda fracción.
La fracción simplificada de $\frac{16}{20}$ es $\frac{4}{5}$.
La segunda fracción dada es $\frac{4}{5}$.
Como ambas fracciones son iguales a $\frac{4}{5}$ en su mínima expresión, son equivalentes.
Respuesta: Sí, la fracción $\frac{16}{20}$ es equivalente a $\frac{4}{5}$ porque al simplificar $\frac{16}{20}$ se obtiene $\frac{4}{5}$.
Solución
Para determinar quién ha leído más, debemos comparar las fracciones $\frac{2}{5}$ y $\frac{3}{7}$. Usaremos el método de productos cruzados.
▷ Paso 1 Multiplicar el numerador de la primera fracción por el denominador de la segunda.
Para $\frac{2}{5}$: $2 \times 7 = 14$
▷ Paso 2 Multiplicar el numerador de la segunda fracción por el denominador de la primera.
Para $\frac{3}{7}$: $3 \times 5 = 15$
▷ Paso 3 Comparar los resultados de las multiplicaciones.
Comparamos 14 y 15.
Como $14 < 15$.
▷ Paso 4 Establecer la relación entre las fracciones originales.
Esto significa que $\frac{2}{5} < \frac{3}{7}$.
Respuesta: El estudiante que ha leído $\frac{3}{7}$ del libro ha leído una mayor parte.
Conclusión
La simplificación y la comparación de fracciones son habilidades fundamentales que consolidan tu comprensión de los números racionales. La simplificación nos permite trabajar con fracciones de una manera más eficiente y clara, asegurando que cada cantidad se exprese en su forma más concisa, evitando confusiones y facilitando cálculos posteriores.
Por otro lado, la capacidad de comparar fracciones es crucial para ordenar y evaluar cantidades. Ya sea que las fracciones compartan el mismo denominador, el mismo numerador o sean completamente diferentes, existen métodos robustos (como el uso del mínimo común múltiplo o los productos cruzados) que nos permiten determinar su valor relativo con precisión. Estas habilidades no solo son académicamente valiosas, sino que tienen aplicaciones prácticas en la toma de decisiones diarias, en la resolución de problemas de ingeniería o en el contexto de tu trabajo con robótica, donde la optimización y la precisión en las medidas son clave. Continúa practicando para dominar estas herramientas esenciales.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar