Conversión de Decimales a Fracción - Ejercicios Resueltos
¡Qué tal amigos de Fisimat!, en nuestro día a día, nos encontramos constantemente con cantidades que no son números enteros: precios de productos, mediciones de longitud o peso, temperaturas, entre otros. Para representar estas "partes de un todo" de una manera práctica y directa, utilizamos los números decimales. Un número decimal es una forma de expresar números no enteros utilizando un punto (o una coma, según la convención regional) para separar la parte entera de la parte fraccionaria. 🤓
La relación entre los números decimales y las fracciones es fundamental en matemáticas. Ambos son dos caras de la misma moneda, dos maneras distintas de representar una misma cantidad. Comprender cómo convertir de uno a otro no solo te facilitará la resolución de problemas en la escuela, sino que también es una habilidad crucial en campos como la ingeniería, la física y la programación, donde la precisión en las mediciones y los cálculos es indispensable. En este artículo, exploraremos los números decimales, su clasificación y la vital conexión que tienen con las fracciones.
Los números decimales son una extensión del sistema de numeración posicional que utilizamos, permitiéndonos representar cantidades más pequeñas que la unidad.
Concepto de Número Decimal
Un número decimal se compone de una parte entera y una parte decimal, separadas por un punto o una coma decimal.
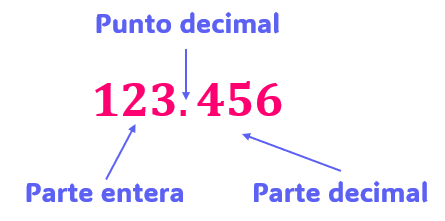
- Parte Entera: Son los dígitos a la izquierda del punto decimal. Representa unidades completas (decenas, centenas, etc.).
- Punto o Coma Decimal: Separa la parte entera de la parte decimal.
- Parte Decimal: Son los dígitos a la derecha del punto decimal. Representan fracciones de una unidad:
- El primer dígito a la derecha del punto son las décimas (partes de diez).
- El segundo dígito son las centésimas (partes de cien).
- El tercer dígito son las milésimas (partes de mil), y así sucesivamente.
Ejemplo: El número $3.25$ se lee "tres con veinticinco centésimas" o "tres punto veinticinco". Significa $3$ unidades enteras y $25$ centésimas de una unidad.
Tipos de Números Decimales
Los números decimales se pueden clasificar según el comportamiento de su parte decimal:
Decimales Exactos
Son aquellos que tienen un número finito de cifras decimales.
Ejemplo: $0.5$, $3.25$, $12.754$
Decimales Periódicos Puros
Son aquellos en los que una o varias cifras se repiten infinitamente después del punto decimal, formando un "periodo". El periodo comienza inmediatamente después del punto decimal. Se indica el periodo con un arco o barra sobre las cifras que se repiten.
Ejemplo: $0.333... = 0.\bar{3}$ (el 3 se repite)
Ejemplo: $1.272727... = 1.\overline{27}$ (el 27 se repite)
Decimales Periódicos Mixtos
Son aquellos en los que hay una parte decimal no periódica (anteperiodo) antes de que comience el periodo.
Ejemplo: $0.1666... = 0.1\bar{6}$ (el 1 es anteperiodo, el 6 es periodo)
Ejemplo: $2.3454545... = 2.3\overline{45}$ (el 3 es anteperiodo, el 45 es periodo)
Decimales No Exactos y No Periódicos (Irracionales)
Son aquellos con un número infinito de cifras decimales que no siguen ningún patrón de repetición. No pueden ser expresados como una fracción simple.
Ejemplo: $\pi \approx 3.14159265...$
Ejemplo: $\sqrt{2} \approx 1.41421356...$
Relación entre Números Decimales y Fracciones
La relación entre decimales y fracciones es bidireccional y fundamental para convertir entre estas representaciones.
🛠 Conversión de Fracción a Decimal
Para convertir una fracción a un número decimal, simplemente se divide el numerador entre el denominador.
Ejemplo: Convertir $\frac{3}{4}$ a decimal.
$$3 \div 4 = 0.75$$
Ejemplo: Convertir $\frac{1}{3}$ a decimal.
$$1 \div 3 = 0.333... = 0.\bar{3}$$
⏳ Conversión de Decimal a Fracción
La forma de convertir un decimal a fracción (también llamada "fracción generatriz") depende del tipo de decimal.
Decimales Exactos a Fracción
- Escribe el número decimal sin el punto como el numerador.
- El denominador será una potencia de 10 (10, 100, 1000, etc.) con tantos ceros como cifras decimales tenga el número original.
- Simplifica la fracción resultante.
Ejemplo: Convertir $0.25$ a fracción.
$$0.25 = \frac{25}{100}$$
Simplificando: $\frac{25 \div 25}{100 \div 25} = \frac{1}{4}$.
Ejemplo: Convertir $3.125$ a fracción.
$$3.125 = \frac{3125}{1000}$$
Simplificando (dividiendo sucesivamente por 5):
$$\frac{3125 \div 5}{1000 \div 5} = \frac{625}{200}$$
$$\frac{625 \div 25}{200 \div 25} = \frac{25}{8}$$
También se puede escribir como número mixto: $3\frac{1}{8}$.
Decimales Periódicos Puros a Fracción
- Escribe el número decimal (sin el punto) hasta el final del primer periodo como numerador.
- Resta la parte entera del número al numerador.
- El denominador estará formado por tantos nueves como cifras tenga el periodo.
- Simplifica la fracción.
Ejemplo: Convertir $0.\bar{3}$ a fracción.
- Número sin punto y hasta el periodo: 3.
- Resta la parte entera (0): $3 - 0 = 3$. (Numerador)
- Un 9 en el denominador porque hay una cifra en el periodo (3).
- Fracción: $\frac{3}{9}$. Simplificando: $\frac{1}{3}$.
Ejemplo: Convertir $1.\overline{27}$ a fracción.
- Número sin punto y hasta el periodo: 127.
- Resta la parte entera (1): $127 - 1 = 126$. (Numerador)
- Dos 9s en el denominador porque hay dos cifras en el periodo (27).
- Fracción: $\frac{126}{99}$. Simplificando (dividiendo por 9): $\frac{126 \div 9}{99 \div 9} = \frac{14}{11}$.
Decimales Periódicos Mixtos a Fracción
- Escribe el número decimal sin el punto hasta el final del primer periodo como numerador.
- Resta la parte del número que está antes del periodo (parte entera y anteperiodo sin el punto) al numerador.
- El denominador estará formado por tantos nueves como cifras tenga el periodo, seguidos de tantos ceros como cifras tenga el anteperiodo.
- Simplifica la fracción.
Ejemplo: Convertir $0.1\bar{6}$ a fracción.
- Número sin punto y hasta el periodo: 16.
- Resta la parte no periódica (01, es decir, 1): $16 - 1 = 15$. (Numerador)
- Un 9 (por el 6 periódico) y un 0 (por el 1 anteperiódico). Denominador: 90.
- Fracción: $\frac{15}{90}$. Simplificando (dividiendo por 15): $\frac{15 \div 15}{90 \div 15} = \frac{1}{6}$.
Ejemplo: Convertir $2.3\overline{45}$ a fracción.
- Número sin punto y hasta el periodo: 2345.
- Resta la parte no periódica (23): $2345 - 23 = 2322$. (Numerador)
- Dos 9s (por el 45 periódico) y un 0 (por el 3 anteperiódico). Denominador: 990.
- Fracción: $\frac{2322}{990}$. Simplificando (dividiendo por 18): $\frac{2322 \div 18}{990 \div 18} = \frac{129}{55}$.
Ejercicios Resueltos de Números decimales y fracciones
Pon a prueba tus conocimientos con estos ejercicios prácticos sobre números decimales y fracciones.
Problema 1. Convierte la fracción $\frac{5}{8}$ a su expresión decimal.
Solución
Para convertir una fracción a decimal, dividimos el numerador entre el denominador.
▷ Paso 1 Realizar la división.
$$5 \div 8$$
$$5.000 \div 8 = 0.625$$
Por lo tanto, la expresión decimal de $\frac{5}{8}$ es $0.625$.
Problema 2. Convierte el número decimal $0.75$ a una fracción irreducible.
Solución
El número $0.75$ es un decimal exacto.
▷ Paso 1 Escribir el número sin el punto como numerador y la potencia de 10 como denominador.
Como tiene dos cifras decimales, el denominador es $10^2 = 100$.
$$\frac{75}{100}$$
▷ Paso 2 Simplificar la fracción resultante.
El MCD de 75 y 100 es 25.
$$\frac{75 \div 25}{100 \div 25} = \frac{3}{4}$$
Por lo tanto, la fracción irreducible de $0.75$ es $\frac{3}{4}$.
Problema 3. Convierte el número decimal $0.\bar{6}$ (cero punto seis periódico) a su fracción generatriz.
Solución
El número $0.\bar{6}$ es un decimal periódico puro.
▷ Paso 1 Escribir el número sin el punto y hasta el final del periodo: 6.
▷ Paso 2 Restar la parte entera (0) al número: $6 - 0 = 6$. (Numerador)
▷ Paso 3 Poner tantos 9s como cifras tenga el periodo. El periodo es '6' (una cifra), entonces el denominador es 9.
$$\frac{6}{9}$$
▷ Paso 4 Simplificar la fracción.
El MCD de 6 y 9 es 3.
$$\frac{6 \div 3}{9 \div 3} = \frac{2}{3}$$
Por lo tanto, la fracción generatriz de $0.\bar{6}$ es $\frac{2}{3}$.
Problema 4. Convierte el número decimal $1.\overline{4}$ (uno punto cuatro periódico) a su fracción generatriz.
Solución
El número $1.\overline{4}$ es un decimal periódico puro.
▷ Paso 1 Escribir el número sin el punto y hasta el final del periodo: 14.
▷ Paso 2 Restar la parte entera (1) al número: $14 - 1 = 13$. (Numerador)
▷ Paso 3 Poner tantos 9s como cifras tenga el periodo. El periodo es '4' (una cifra), entonces el denominador es 9.
$$\frac{13}{9}$$
La fracción $\frac{13}{9}$ ya es irreducible.
Por lo tanto, la fracción generatriz de $1.\overline{4}$ es $\frac{13}{9}$.
Problema 5. Convierte el número decimal $0.2\bar{5}$ (cero punto dos cinco periódico) a su fracción generatriz.
Solución
El número $0.2\bar{5}$ es un decimal periódico mixto.
▷ Paso 1 Escribir el número sin el punto hasta el final del periodo: 25.
▷ Paso 2 Restar la parte no periódica (parte entera y anteperiodo sin el punto, es decir, 02 o 2): $25 - 2 = 23$. (Numerador)
▷ Paso 3 El denominador tendrá tantos 9s como cifras en el periodo (un 5, un 9) y tantos 0s como cifras en el anteperiodo (un 2, un 0). Denominador: 90.
$$\frac{23}{90}$$
La fracción $\frac{23}{90}$ ya es irreducible (23 es número primo, y 90 no es múltiplo de 23).
Por lo tanto, la fracción generatriz de $0.2\bar{5}$ es $\frac{23}{90}$.
Problema 6. Convierte el número decimal $3.1\overline{2}$ (tres punto uno dos periódico) a su fracción generatriz.
Solución
El número $3.1\overline{2}$ es un decimal periódico mixto.
▷ Paso 1 Escribir el número sin el punto hasta el final del periodo: 312.
▷ Paso 2 Restar la parte no periódica (parte entera y anteperiodo sin el punto, es decir, 31): $312 - 31 = 281$. (Numerador)
▷ Paso 3 El denominador tendrá tantos 9s como cifras en el periodo (un 2, un 9) y tantos 0s como cifras en el anteperiodo (un 1, un 0). Denominador: 90.
$$\frac{281}{90}$$
La fracción $\frac{281}{90}$ ya es irreducible (281 es número primo).
Por lo tanto, la fracción generatriz de $3.1\overline{2}$ es $\frac{281}{90}$.
Problema 7. ¿Qué es mayor, $\frac{3}{5}$ o $0.65$? Justifica tu respuesta.
Solución
Para comparar una fracción con un decimal, podemos convertir la fracción a decimal o el decimal a fracción. Convertiremos la fracción a decimal.
▷ Paso 1 Convertir la fracción $\frac{3}{5}$ a decimal.
$$3 \div 5 = 0.6$$
▷ Paso 2 Comparar los números decimales.
Comparamos $0.6$ y $0.65$.
Podemos añadir un cero a $0.6$ para igualar el número de cifras decimales: $0.60$.
Ahora comparamos $0.60$ y $0.65$.
Como $0.60 < 0.65$.
Por lo tanto, $0.65$ es mayor que $\frac{3}{5}$.
Problema 8. Ordena de menor a mayor los siguientes números: $0.8, \frac{4}{5}, 0.\bar{8}$.
Solución
Para ordenar, convertiremos todas las expresiones a decimales para facilitar la comparación.
▷ Paso 1 Convertir cada número a decimal.
$0.8$: Ya está en decimal.
$\frac{4}{5}$: $4 \div 5 = 0.8$.
$0.\bar{8}$: Es $0.888...$
▷ Paso 2 Comparar los valores decimales.
Tenemos:
$0.800$ (para $0.8$)
$0.800$ (para $\frac{4}{5}$)
$0.888...$ (para $0.\bar{8}$)
▷ Paso 3 Ordenar de menor a mayor.
En este caso, $0.8$ y $\frac{4}{5}$ son iguales. Ambos son menores que $0.\bar{8}$.
Orden: $0.8 = \frac{4}{5} < 0.\bar{8}$.
Problema 9. Un recipiente contiene $0.75$ litros de agua. ¿Qué fracción de un litro representa esta cantidad?
Solución
Convertiremos el número decimal $0.75$ a una fracción.
▷ Paso 1 Escribir el número sin el punto como numerador y la potencia de 10 como denominador.
$$0.75 = \frac{75}{100}$$
▷ Paso 2 Simplificar la fracción.
El MCD de 75 y 100 es 25.
$$\frac{75 \div 25}{100 \div 25} = \frac{3}{4}$$
Respuesta: La cantidad de agua representa $\frac{3}{4}$ de un litro.
Conclusión
Los números decimales y las fracciones son dos representaciones interconectadas de los números racionales, ofreciendo flexibilidad para expresar cantidades en diferentes contextos. La habilidad de convertir entre ellos es un pilar fundamental en la aritmética, permitiendo un manejo más eficiente y preciso de la información numérica.
Desde la claridad de un decimal exacto para medidas directas hasta la representación exacta de un periódico mediante una fracción, cada tipo tiene su propósito. Dominar las técnicas de conversión y comprender su relación te brinda una herramienta poderosa para resolver problemas matemáticos y aplicarlos en áreas como la ingeniería, donde la precisión en el diseño y los cálculos es vital, o en la programación, donde la representación numérica eficiente es clave. Esta interconexión refuerza la idea de que las matemáticas son un lenguaje coherente y adaptable a diversas necesidades. 🥳
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta
Estos temas te pueden interesar