Cuartiles, Deciles y Percentiles - Ejercicios Resueltos
¡Hola, amigos de Fisimat! 👋 ¿Alguna vez te has preguntado cómo los estadísticos y científicos de datos entienden la distribución de un conjunto de datos más allá del simple promedio? Mientras que la media, la mediana y la moda nos dan una idea del centro de los datos, a menudo necesitamos una visión más granular. Queremos saber cómo se posiciona un dato específico en relación con el resto. Aquí es donde entran en juego las medidas de posición no central: los cuartiles, deciles y percentiles. 📊
Estas herramientas son como marcadores en una regla. No solo nos dicen dónde está el centro, sino que también dividen nuestros datos en segmentos iguales, permitiéndonos entender la dispersión, identificar valores atípicos y comparar puntos de datos de una manera mucho más sofisticada. Desde calificar exámenes estandarizados hasta analizar la distribución de la riqueza en un país, estas medidas son fundamentales. En este artículo, desglosaremos cada uno de estos conceptos de una manera clara y pedagógica, con ejemplos guiados paso a paso para que te conviertas en un experto. ¡Empecemos! 🚀
- ¿Qué son las Medidas de Posición o Cuantiles?
- Cuartiles: Dividiendo los Datos en Cuatro Partes Iguales 🍰
- Deciles: Dividiendo en Diez Franjas Iguales 📜
- Percentiles: La Máxima Precisión (100 Divisiones) 🎯
- Ejercicios Adicionales Resueltos
- Visualizando las Medidas de Posición con Gráficos 📊
- Conclusión: Más Allá de los Promedios
¿Qué son las Medidas de Posición o Cuantiles?
Antes de sumergirnos en cada término específico, es crucial entender el concepto que los agrupa a todos: los cuantiles. Imagina que tienes una fila de personas ordenadas por altura, de la más baja a la más alta. Los cuantiles son los puntos de corte que dividen a esta fila de personas en grupos de igual tamaño.

Cuantiles
Los cuantiles son valores de una variable que dividen la distribución de frecuencias de un conjunto de datos ordenados en un número de partes iguales. Son esencialmente puntos de corte que nos ayudan a entender dónde se encuentra un dato en particular dentro del espectro completo de los datos. Los tipos más comunes de cuantiles son los cuartiles, deciles y percentiles.
La idea principal es simple: ordenar los datos de menor a mayor y luego encontrar los valores que los dividen en los fragmentos que nos interesan. Si dividimos en 4 partes, hablamos de cuartiles. Si dividimos en 10, son deciles. Y si dividimos en 100, son percentiles. ¡Así de fácil! Ahora, veamos cada uno en detalle.
Cuartiles: Dividiendo los Datos en Cuatro Partes Iguales 🍰
Los cuartiles son, quizás, los cuantiles más utilizados. Como su nombre indica, dividen un conjunto de datos ordenado en cuatro partes iguales. Cada una de estas partes contiene el 25% de los datos. Tenemos tres cuartiles que actúan como puntos de división:
- Primer Cuartil (Q1): Es el valor por debajo del cual se encuentra el 25% de los datos. Es, a su vez, el valor que supera al 75% restante.
- Segundo Cuartil (Q2): ¡Un viejo conocido! Q2 es exactamente la mediana del conjunto de datos. Divide los datos en dos mitades iguales, con el 50% de los datos por debajo y el 50% por encima.
- Tercer Cuartil (Q3): Es el valor que deja por debajo al 75% de los datos y por encima al 25%.
Visualmente, si tienes una línea de datos ordenados, los cuartiles se verían así:
Mínimo --- (25%) --- Q1 --- (25%) --- Q2 (Mediana) --- (25%) --- Q3 --- (25%) --- Máximo
Rango Intercuartílico (IQR)
Una aplicación muy poderosa de los cuartiles es el cálculo del Rango Intercuartílico (IQR, por sus siglas en inglés). Esta es una medida de dispersión estadística que nos dice qué tan extendido está el 50% central de los datos.
Rango Intercuartílico (IQR)
El Rango Intercuartílico es la diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1). La fórmula es: \[ IQR = Q_3 - Q_1 \]
El IQR es especialmente útil porque no se ve afectado por valores atípicos (outliers) en los extremos de la distribución, lo que lo convierte en una medida de dispersión más robusta que el rango total (máximo - mínimo).
Cómo Calcular los Cuartiles para Datos No Agrupados
Calcular los cuartiles para una lista de números es bastante sencillo. El método varía ligeramente si tienes un número par o impar de datos.
Pasos a seguir:
- Ordena todos los datos de menor a mayor.
- Encuentra la mediana (Q2). Este será el valor central si el número de datos (n) es impar, o el promedio de los dos valores centrales si n es par.
- Para Q1: Encuentra la mediana de la mitad inferior de los datos (los valores a la izquierda de Q2, sin incluir Q2 si n es impar).
- Para Q3: Encuentra la mediana de la mitad superior de los datos (los valores a la derecha de Q2, sin incluir Q2 si n es impar).
Vamos a verlo con un ejemplo práctico.
Ejemplo 1: Cálculo de Cuartiles (Número Impar de Datos)
Las calificaciones de 11 estudiantes en un examen de física son: 88, 92, 75, 68, 81, 95, 78, 85, 89, 90, 72. Encuentra Q1, Q2, Q3 y el IQR.
Solución:
Paso 1: Ordenar los datos
Primero, ordenamos las calificaciones de menor a mayor:
\( 68, 72, 75, 78, 81, 85, 88, 89, 90, 92, 95 \)
Paso 2: Calcular Q2 (la Mediana)
Tenemos \(n = 11\) datos (un número impar). La mediana es el valor en la posición central, que se calcula como \( \frac{n+1}{2} = \frac{11+1}{2} = 6 \). El sexto dato es la mediana.
Datos: 68, 72, 75, 78, 81, 85, 88, 89, 90, 92, 95
Por lo tanto, \( Q_2 = 85 \).
Paso 3: Calcular Q1
Ahora tomamos la mitad inferior de los datos (los que están a la izquierda de Q2):
\( 68, 72, 75, 78, 81 \)
La mediana de este subconjunto es el valor central (el tercer valor), que es 75.
Por lo tanto, \( Q_1 = 75 \).
Paso 4: Calcular Q3
Tomamos la mitad superior de los datos (a la derecha de Q2):
\( 88, 89, 90, 92, 95 \)
La mediana de este subconjunto es el valor central (el tercer valor), que es 90.
Por lo tanto, \( Q_3 = 90 \).
Paso 5: Calcular el IQR
Finalmente, calculamos el rango intercuartílico:
\( IQR = Q_3 - Q_1 = 90 - 75 = 15 \)
Esto nos dice que el 50% central de las calificaciones se encuentra en un rango de 15 puntos. 🎯
Cómo Calcular los Cuartiles para Datos Agrupados
Cuando trabajamos con datos agrupados en una tabla de frecuencias, no conocemos los valores exactos, solo los intervalos. En este caso, usamos una fórmula para estimar los cuartiles.
La fórmula general es:
\[ Q_k = L_i + \left( \frac{\frac{kN}{4} - F_{i-1}}{f_i} \right) \cdot A \]
Donde:
- \( k \): El número del cuartil que queremos encontrar (1, 2 o 3).
- \( L_i \): Límite inferior del intervalo donde se encuentra el cuartil.
- \( N \): Número total de datos.
- \( F_{i-1} \): Frecuencia acumulada del intervalo anterior al intervalo del cuartil.
- \( f_i \): Frecuencia absoluta del intervalo del cuartil.
- \( A \): Amplitud del intervalo (\( A = \text{Límite Superior} - \text{Límite Inferior} \)).
El primer paso es encontrar la "clase del cuartil" buscando en la columna de frecuencia acumulada el primer valor que sea mayor o igual a \( \frac{kN}{4} \).
Ejemplo 2: Cálculo de Cuartiles (Datos Agrupados)
Se midió la altura (en cm) de 50 estudiantes, y los datos se agruparon en la siguiente tabla de frecuencias. Calcula Q1 y Q3.
| Altura (cm) | Frecuencia (fi) | Frecuencia Acumulada (Fi) |
|---|---|---|
| [150, 155) | 6 | 6 |
| [155, 160) | 10 | 16 |
| [160, 165) | 15 | 31 |
| [165, 170) | 12 | 43 |
| [170, 175) | 7 | 50 |
Solución:
Cálculo de Q1 (k=1):
1. Encontrar la posición: \( \frac{1 \cdot N}{4} = \frac{1 \cdot 50}{4} = 12.5 \)
Buscamos en la columna de Frecuencia Acumulada (Fi) el primer valor mayor o igual a 12.5. Este valor es 16, que corresponde al intervalo [155, 160).
2. Identificar los datos para la fórmula:
- Clase de Q1: [155, 160)
- \( L_i = 155 \)
- \( N = 50 \)
- \( F_{i-1} = 6 \) (la frecuencia acumulada del intervalo anterior)
- \( f_i = 10 \) (la frecuencia absoluta del intervalo de Q1)
- \( A = 160 - 155 = 5 \)
3. Aplicar la fórmula:
\[ Q_1 = 155 + \left( \frac{12.5 - 6}{10} \right) \cdot 5 \]
\[ Q_1 = 155 + \left( \frac{6.5}{10} \right) \cdot 5 \]
\[ Q_1 = 155 + 0.65 \cdot 5 \]
\[ Q_1 = 155 + 3.25 = 158.25 \text{ cm} \]
Cálculo de Q3 (k=3):
1. Encontrar la posición: \( \frac{3 \cdot N}{4} = \frac{3 \cdot 50}{4} = 37.5 \)
Buscamos en la columna Fi el primer valor mayor o igual a 37.5. Este es 43, que corresponde al intervalo [165, 170).
2. Identificar los datos para la fórmula:
- Clase de Q3: [165, 170)
- \( L_i = 165 \)
- \( N = 50 \)
- \( F_{i-1} = 31 \)
- \( f_i = 12 \)
- \( A = 5 \)
3. Aplicar la fórmula:
\[ Q_3 = 165 + \left( \frac{37.5 - 31}{12} \right) \cdot 5 \]
\[ Q_3 = 165 + \left( \frac{6.5}{12} \right) \cdot 5 \]
\[ Q_3 \approx 165 + 0.5417 \cdot 5 \]
\[ Q_3 \approx 165 + 2.71 = 167.71 \text{ cm} \]
Deciles: Dividiendo en Diez Franjas Iguales 📜
Si los cuartiles son útiles, los deciles nos dan una visión aún más detallada. Los deciles dividen un conjunto de datos ordenado en diez partes iguales. Cada parte representa el 10% de los datos.
Deciles
Hay nueve deciles (D1, D2, ..., D9) que actúan como puntos de corte. El decil \(D_k\) es el valor que deja por debajo al \(10 \cdot k\%\) de los datos. Por ejemplo, D3 es el valor por debajo del cual se encuentra el 30% de los datos. Es importante notar que D5 es lo mismo que Q2 y la mediana.
Cómo Calcular los Deciles
El proceso es muy similar al de los cuartiles, solo cambia el divisor en las fórmulas.
Para datos no agrupados, la posición del decil \(D_k\) se encuentra con la fórmula \( \text{Posición} = \frac{k(n+1)}{10} \). Si la posición es un decimal, se interpola entre los valores correspondientes.
Para datos agrupados, la fórmula es:
\[ D_k = L_i + \left( \frac{\frac{kN}{10} - F_{i-1}}{f_i} \right) \cdot A \]
Como puedes ver, es idéntica a la fórmula de los cuartiles, excepto que el denominador es 10 en lugar de 4. ¡Aprendes una y las sabes todas!
Ejemplo 3: Cálculo de Deciles (Datos Agrupados)
Usando la misma tabla de alturas de 50 estudiantes del ejemplo anterior, calcula el decil 7 (D7).
Solución:
Cálculo de D7 (k=7):
1. Encontrar la posición: \( \frac{7 \cdot N}{10} = \frac{7 \cdot 50}{10} = 35 \)
Buscamos en la columna Fi el primer valor mayor o igual a 35. Este valor es 43, que corresponde al intervalo [165, 170).
2. Identificar los datos para la fórmula:
- Clase de D7: [165, 170)
- \( L_i = 165 \)
- \( N = 50 \)
- \( F_{i-1} = 31 \)
- \( f_i = 12 \)
- \( A = 5 \)
3. Aplicar la fórmula:
\[ D_7 = 165 + \left( \frac{35 - 31}{12} \right) \cdot 5 \]
\[ D_7 = 165 + \left( \frac{4}{12} \right) \cdot 5 \]
\[ D_7 = 165 + \frac{1}{3} \cdot 5 \]
\[ D_7 \approx 165 + 1.67 = 166.67 \text{ cm} \]
Esto significa que el 70% de los estudiantes mide 166.67 cm o menos. 📏
Percentiles: La Máxima Precisión (100 Divisiones) 🎯
Finalmente, llegamos a la medida de posición más granular: los percentiles. Estos dividen un conjunto de datos ordenado en cien partes iguales. Cada parte representa el 1% de los datos.
Percentiles
Hay 99 percentiles (P1, P2, ..., P99). El percentil \(P_k\) es el valor que deja por debajo al \(k\%\) de los datos. Los percentiles son muy comunes en informes de resultados de pruebas estandarizadas (como el SAT o GRE) y en tablas de crecimiento pediátrico.
La relación entre los tres tipos de cuantiles es directa:
- \( Q_1 = P_{25} \)
- \( Q_2 = D_5 = P_{50} = \text{Mediana} \)
- \( Q_3 = P_{75} \)
- \( D_1 = P_{10} \), \( D_2 = P_{20} \), etc.
Cómo Calcular los Percentiles
Las fórmulas siguen la misma lógica que ya hemos visto.
Para datos no agrupados, la posición del percentil \(P_k\) se encuentra con \( \text{Posición} = \frac{k(n+1)}{100} \).
Para datos agrupados, la fórmula es:
\[ P_k = L_i + \left( \frac{\frac{kN}{100} - F_{i-1}}{f_i} \right) \cdot A \]
El único cambio es el denominador, que ahora es 100.
Ejemplo 4: Cálculo de Percentiles (Datos Agrupados)
Con la misma tabla de alturas, un estudiante quiere saber si está en el 90% superior de altura de su clase. Para ello, necesitamos calcular el percentil 90 (P90).
Solución:
Cálculo de P90 (k=90):
1. Encontrar la posición: \( \frac{90 \cdot N}{100} = \frac{90 \cdot 50}{100} = 45 \)
Buscamos en la columna Fi el primer valor mayor o igual a 45. Este es 50, que corresponde al intervalo [170, 175).
2. Identificar los datos para la fórmula:
- Clase de P90: [170, 175)
- \( L_i = 170 \)
- \( N = 50 \)
- \( F_{i-1} = 43 \)
- \( f_i = 7 \)
- \( A = 5 \)
3. Aplicar la fórmula:
\[ P_{90} = 170 + \left( \frac{45 - 43}{7} \right) \cdot 5 \]
\[ P_{90} = 170 + \left( \frac{2}{7} \right) \cdot 5 \]
\[ P_{90} \approx 170 + 0.2857 \cdot 5 \]
\[ P_{90} \approx 170 + 1.43 = 171.43 \text{ cm} \]
Esto significa que el 90% de los estudiantes mide 171.43 cm o menos. Si el estudiante mide más que eso, ¡está en el 10% más alto! 🏆
Ejercicios Adicionales Resueltos
Ejemplo 5: Cálculo de Cuartiles (Número Par de Datos)
Una tienda de electrónica registra el número de portátiles vendidos diariamente durante 12 días. Los datos son: 15, 8, 12, 10, 22, 17, 9, 11, 16, 14, 20, 18. Calcula los tres cuartiles (Q1, Q2, Q3) y el rango intercuartílico (IQR).
Solución:
Paso 1: Ordenar los datos
Primero, organizamos el número de ventas de menor a mayor:
\( 8, 9, 10, 11, 12, 14, 15, 16, 17, 18, 20, 22 \)
Paso 2: Calcular Q2 (la Mediana)
Tenemos \(n = 12\) datos (un número par). La mediana es el promedio de los dos valores centrales. Las posiciones centrales son \(n/2 = 12/2 = 6\) y \(n/2 + 1 = 7\).
Datos: 8, 9, 10, 11, 12, 14, 15, 16, 17, 18, 20, 22
Los valores en estas posiciones son 14 y 15.
\[ Q_2 = \frac{14 + 15}{2} = 14.5 \]
Paso 3: Calcular Q1
Tomamos la mitad inferior de los datos (los valores a la izquierda de la mediana):
\( 8, 9, 10, 11, 12, 14 \)
Como este subconjunto tiene 6 datos (par), Q1 es el promedio de los dos valores centrales (el tercero y el cuarto): 10 y 11.
\[ Q_1 = \frac{10 + 11}{2} = 10.5 \]
Paso 4: Calcular Q3
Ahora, tomamos la mitad superior de los datos (a la derecha de la mediana):
\( 15, 16, 17, 18, 20, 22 \)
De nuevo, tenemos 6 datos. Q3 es el promedio de los dos valores centrales (el tercero y el cuarto): 17 y 18.
\[ Q_3 = \frac{17 + 18}{2} = 17.5 \]
Paso 5: Calcular el IQR
Calculamos la diferencia entre Q3 y Q1:
\( IQR = Q_3 - Q_1 = 17.5 - 10.5 = 7 \)
El 50% central de las ventas diarias de portátiles varía en 7 unidades. 💻
Ejemplo 6: Encontrando un Percentil Específico (Datos no Agrupados)
Las puntuaciones de 15 estudiantes en una prueba de aptitud son: 45, 72, 88, 56, 65, 78, 91, 82, 75, 60, 50, 85, 79, 81, 68. Un estudiante necesita estar en el percentil 80 para calificar para un programa especial. ¿Qué puntuación mínima necesita?
Solución:
Paso 1: Ordenar los datos
Ordenamos las puntuaciones de menor a mayor:
\( 45, 50, 56, 60, 65, 68, 72, 75, 78, 79, 81, 82, 85, 88, 91 \)
Paso 2: Calcular la posición del percentil 80 (P80)
Usamos la fórmula para la posición de un percentil en datos no agrupados, donde \(k=80\) y \(n=15\):
\[ \text{Posición} = \frac{k(n+1)}{100} = \frac{80(15+1)}{100} \]
\[ \text{Posición} = \frac{80 \cdot 16}{100} = \frac{1280}{100} = 12.8 \]
Paso 3: Interpolar para encontrar el valor
Una posición de 12.8 significa que el valor de P80 está entre el 12º y el 13º dato. El 12º dato es 82 y el 13º es 85.
El valor de P80 es el 12º valor más el 80% (0.8) de la diferencia entre el 13º y el 12º valor.
\[ P_{80} = \text{Valor}_{12} + 0.8 \times (\text{Valor}_{13} - \text{Valor}_{12}) \]
\[ P_{80} = 82 + 0.8 \times (85 - 82) \]
\[ P_{80} = 82 + 0.8 \times 3 \]
\[ P_{80} = 82 + 2.4 = 84.4 \]
Por lo tanto, un estudiante necesita obtener una puntuación de al menos 84.4 para estar en el percentil 80. 🎓
Ejemplo 7: Cálculo de Deciles (Datos Agrupados)
Se realizó una encuesta sobre el tiempo diario (en minutos) que 100 personas dedican a hacer ejercicio. Los resultados se muestran en la siguiente tabla. Calcula el decil 4 (D4).
| Tiempo (minutos) | Frecuencia (fi) | Frecuencia Acumulada (Fi) |
|---|---|---|
| [0, 20) | 15 | 15 |
| [20, 40) | 25 | 40 |
| [40, 60) | 35 | 75 |
| [60, 80) | 20 | 95 |
| [80, 100) | 5 | 100 |
Solución:
Cálculo de D4 (k=4):
1. Encontrar la posición:
Tenemos \(N=100\). La posición para el decil 4 es: \( \frac{4 \cdot N}{10} = \frac{4 \cdot 100}{10} = 40 \).
Buscamos en la columna de Frecuencia Acumulada (Fi) el primer valor que sea mayor o igual a 40. El valor es exactamente 40, que corresponde al intervalo [20, 40).
2. Identificar los datos para la fórmula:
- Clase de D4: [20, 40)
- \( L_i = 20 \) (Límite inferior)
- \( N = 100 \)
- \( F_{i-1} = 15 \) (Frecuencia acumulada del intervalo anterior)
- \( f_i = 25 \) (Frecuencia absoluta del intervalo de D4)
- \( A = 40 - 20 = 20 \) (Amplitud del intervalo)
3. Aplicar la fórmula del decil:
\[ D_k = L_i + \left( \frac{\frac{kN}{10} - F_{i-1}}{f_i} \right) \cdot A \]
\[ D_4 = 20 + \left( \frac{40 - 15}{25} \right) \cdot 20 \]
\[ D_4 = 20 + \left( \frac{25}{25} \right) \cdot 20 \]
\[ D_4 = 20 + 1 \cdot 20 = 40 \]
El decil 4 es de 40 minutos. Esto significa que el 40% de las personas encuestadas hacen ejercicio 40 minutos o menos al día. 🏋️♀️
Ejemplo 8: Encontrando el Valor de un Percentil (Datos Agrupados)
Utilizando la misma tabla de tiempo de ejercicio del ejemplo anterior, una aplicación de fitness quiere premiar a los usuarios que se encuentran por encima del percentil 85. ¿Cuál es el tiempo mínimo de ejercicio diario para recibir el premio?
Solución:
Cálculo de P85 (k=85):
1. Encontrar la posición:
La posición para el percentil 85 es: \( \frac{85 \cdot N}{100} = \frac{85 \cdot 100}{100} = 85 \).
Buscamos en la columna Fi el primer valor mayor o igual a 85. Este valor es 95, que corresponde al intervalo [60, 80).
2. Identificar los datos para la fórmula:
- Clase de P85: [60, 80)
- \( L_i = 60 \)
- \( N = 100 \)
- \( F_{i-1} = 75 \)
- \( f_i = 20 \)
- \( A = 20 \)
3. Aplicar la fórmula del percentil:
\[ P_k = L_i + \left( \frac{\frac{kN}{100} - F_{i-1}}{f_i} \right) \cdot A \]
\[ P_{85} = 60 + \left( \frac{85 - 75}{20} \right) \cdot 20 \]
\[ P_{85} = 60 + \left( \frac{10}{20} \right) \cdot 20 \]
\[ P_{85} = 60 + 0.5 \cdot 20 = 60 + 10 = 70 \]
El tiempo mínimo de ejercicio para recibir el premio es de 70 minutos diarios. ¡Cualquiera que entrene por encima de esa marca es un usuario top! 🏅
Visualizando las Medidas de Posición con Gráficos 📊
Una imagen vale más que mil palabras, y en estadística, un buen gráfico vale más que mil números. Para que estos conceptos cobren vida, veamos cómo se representan los cuartiles, deciles y percentiles utilizando gráficos generados con Python, una herramienta fundamental en el análisis de datos.
El Diagrama de Caja: El Rey de los Cuartiles
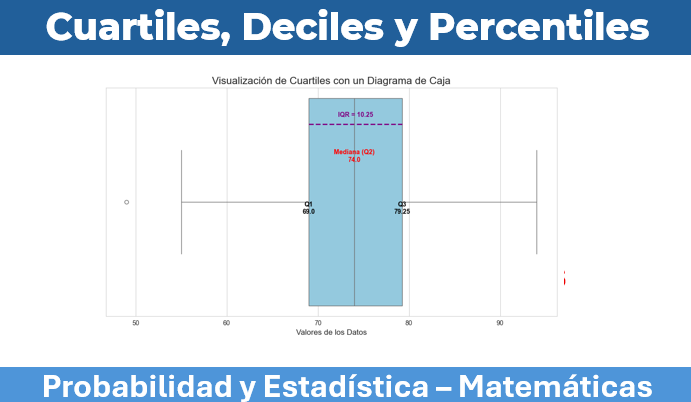
La forma más directa y efectiva de visualizar los cuartiles es a través de un diagrama de caja (o Box Plot). Este gráfico resume la distribución de los datos mostrando los puntos clave de una manera muy limpia.
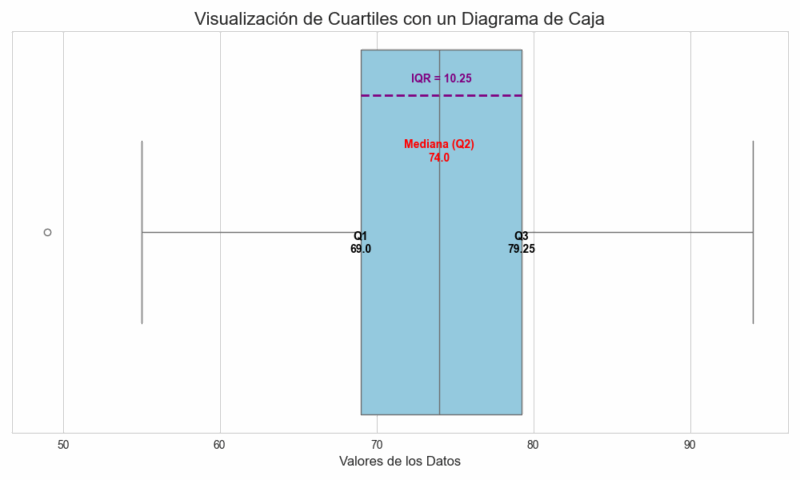
Explicación del gráfico:
- La Caja Central: El corazón del gráfico es el rectángulo. La longitud de esta caja representa el Rango Intercuartílico (IQR), que contiene el 50% central de todos los datos. Es una medida de dispersión muy robusta.
- Líneas de la Caja: El borde izquierdo de la caja marca el Primer Cuartil (Q1), el punto por debajo del cual se encuentra el 25% de los datos. El borde derecho marca el Tercer Cuartil (Q3), que deja al 75% de los datos por debajo.
- La Línea Roja (Mediana): La línea que divide la caja es la Mediana (Q2 o Percentil 50). Su posición nos indica si el 50% central de los datos está sesgado hacia valores más altos o más bajos.
- Los "Bigotes": Las líneas que se extienden desde la caja (llamadas bigotes) muestran el resto de la distribución de los datos, generalmente hasta 1.5 veces el IQR. Los puntos más allá de los bigotes suelen considerarse valores atípicos.
Histograma: Mapeando Deciles y Percentiles
Para tener una visión más granular, podemos usar un histograma. Este gráfico nos muestra la frecuencia de los datos en diferentes intervalos. Al superponer líneas verticales, podemos señalar la ubicación exacta de deciles y percentiles, viendo cuántos datos quedan a la izquierda de cada marcador.
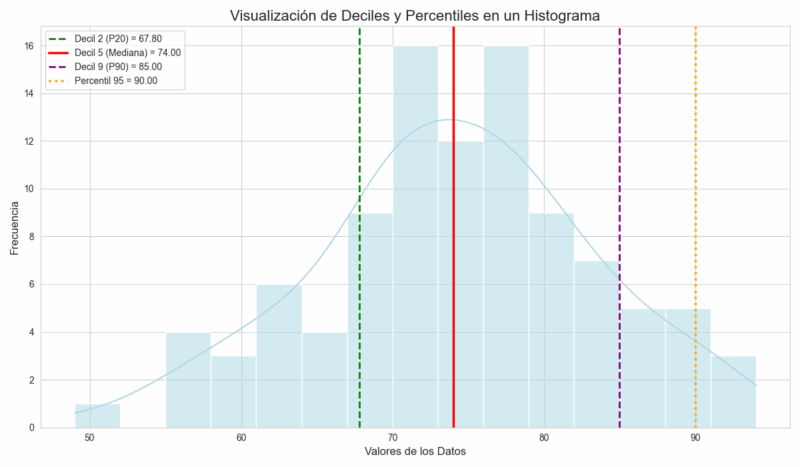
Explicación del gráfico:
- Las Barras (Histograma): Cada barra representa la cantidad de datos que caen dentro de un rango específico. En este caso, vemos que la mayoría de los datos se concentran alrededor del centro de la distribución.
- Líneas Verticales: Cada línea de color es un marcador de posición. Por ejemplo:
- La línea verde (Decil 2 / P20) nos muestra el valor que supera al 20% de los datos.
- La línea roja (Mediana / P50) divide los datos en dos mitades exactas.
- La línea morada (Decil 9 / P90) indica el umbral del 10% superior. Solo un 10% de los datos tienen un valor mayor que este.
- La línea naranja (Percentil 95) nos muestra el valor que solo el 5% de los datos logra superar. ¡Estar aquí es estar en la élite de los datos!
Conclusión: Más Allá de los Promedios
Como hemos visto, los cuartiles, deciles y percentiles son herramientas increíblemente poderosas que nos ofrecen una comprensión profunda de la estructura de nuestros datos. Nos permiten ir más allá de una simple medida central y analizar la posición relativa de cualquier valor dentro de un conjunto. Ya sea para identificar la dispersión del 50% central de los datos con el IQR, segmentar una población en grupos de ingresos con deciles, o situar un resultado en un contexto competitivo con percentiles, estos cuantiles son esenciales en el arsenal de cualquier persona que trabaje con datos.
La próxima vez que escuches "estás en el percentil 95", sabrás exactamente lo que significa: que has superado al 95% de los demás. Y ahora, también sabes cómo calcularlo. ¡Felicidades por dominar estas medidas fundamentales de la estadística descriptiva! 🎉
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar