Derivadas de Funciones Exponenciales

Para aprender a derivar funciones exponenciales, es importante tener en cuenta las fórmulas que se utilizan para este proceso, no son complicadas de aprender, y solamente necesitamos el uso del álgebra para poder resolver sin problemas 😀

De inicio también es importante conocer las derivadas básicas algebraicas, la derivada de una suma, de una potencia, de un producto y de una división. Teniendo estos puntos bien, no hay más complicaciones.

Contenidos

¿De dónde proviene e ?
Fórmulas para las Derivadas de Funciones Exponenciales
Derivadas Exponenciales Resueltas

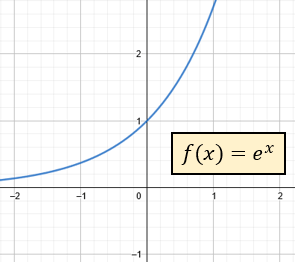
¿De dónde proviene e ?

El número e es un número irracional y famoso, es prácticamente uno de los números más importantes en matemáticas. Los primeros dígitos son:

2,7182818284590452353602874713527 (sigue y sigue ....)

A menudo es conocido como el número de Euler, por el descubrimiento del matemático Leonhard Euler (se pronuncia "Oiler" )

e es la base de los logaritmos naturales o neperianos (inventado por el matemático John Naper)
e se encuentra en muchas áreas de ciencia interesantes.

e también se puede definir mediante un límite de la siguiente manera:

$\displaystyle e=\underset{x\to 0}{\mathop{\lim }}\,{{\left( 1+x \right)}^{\frac{1}{x}}}=2.7182818284...$

Fórmulas para las Derivadas de Funciones Exponenciales

$\displaystyle \frac{d}{dx}{{e}^{x}}={{e}^{x}}$

$\displaystyle \frac{d}{dx}{{a}^{x}}={{a}^{x}}\ln a$

Si en lugar de "x" tuviéramos funciones, entonces las fórmulas de derivadas quedarían de la siguiente forma

$\displaystyle \frac{d}{dx}{{e}^{f(x)}}={{e}^{f(x)}}\cdot f'(x)$

$\displaystyle \frac{d}{dx}{{a}^{f(x)}}={{a}^{f(x)}}\cdot f'(x)\cdot \ln a$

Derivadas Exponenciales Resueltas

Es posible que viendo las fórmulas anteriores pueda ser confuso, ya que muchos profesores o docentes suelen compartirnos algún formulario. En esta ocasión trataremos de explicar paso a paso cada ejemplo para evitar que haya problemas, y no cause confusión con la explicación de tu profesor. 😀

Ejemplo 1. Resuelva la siguiente derivada

$\displaystyle f(x)={{x}^{3}}{{e}^{x}}$

Solución:

Al haber dos funciones que se están multiplicando tendremos que aplicar la regla de la derivada de un producto, es decir:

$\displaystyle f'(x)=\frac{d}{dx}({{x}^{3}}){{e}^{x}}+{{x}^{3}}\frac{d}{dx}({{e}^{x}})$

Aplicando la derivada para x³

$\displaystyle f'(x)=3{{x}^{2}}{{e}^{x}}+{{x}^{3}}\frac{d}{dx}({{e}^{x}})$

Aplicando la derivada para e^x , que sería la misma derivada es decir, nos daría el mismo valor. Esto es porque la fórmula así lo indica.

$\displaystyle f'(x)=3{{x}^{2}}{{e}^{x}}+{{x}^{3}}{{e}^{x}}$

Ahora solamente nos queda factorizar, pero ¡Atención!, hasta este punto ya está derivado toda la función, solamente factorizaremos para ordenar mejor el resultado.

▶️ Resultado:

$\displaystyle f'(x)={{x}^{2}}{{e}^{x}}(3+x)$

Listo 😀

Ejemplo 2. Resuelva la siguiente derivada

$\displaystyle f(x)={{e}^{4{{x}^{3}}}}$

Solución:

En este caso vemos a una función exponencial, observamos que tiene de exponente al 4x³ , esto será de vital importancia porque la fórmula para una función exponencial de una función es la siguiente:

$\displaystyle \frac{d}{dx}{{e}^{f(x)}}={{e}^{f(x)}}\cdot f'(x)$

Es decir, tenemos que derivar a la función 4x³, si derivamos esto nos queda:

$\displaystyle f'(x)={{e}^{4{{x}^{3}}}}\cdot (12{{x}^{2}})$

Qué finalmente sería:

▶️ Resultado:

$\displaystyle f'(x)=12{{x}^{2}}{{e}^{4{{x}^{3}}}}$

Ejemplo 3. Resuelva la siguiente derivada

$\displaystyle y={{5}^{4{{x}^{3}}}}$

Solución:

En esta función vemos que no hay una "e" pero si hay una constante elevada a una función, esto lo solucionaremos con la siguiente regla:

$\displaystyle \frac{d}{dx}{{a}^{f(x)}}={{a}^{f(x)}}\cdot f'(x)\cdot \ln a$

Como ya hemos resuelto la derivada de 4x³ en el ejercicio anterior, entonces solamente expresaremos el resultado. ¡Así de fácil! 😎

$\displaystyle y'={{5}^{4{{x}^{3}}}}\cdot (12{{x}^{2}})\cdot \ln 5$

Ordenando obtendremos el resultado de manera formal

▶️ Resultado:

$\displaystyle y'=12(\ln 5){{x}^{2}}{{5}^{4{{x}^{3}}}}$

Ejemplo 4. Resuelva la siguiente derivada

$\displaystyle y={{e}^{t\cdot sen(4t)}}$

Solución:

Nos encontramos con la derivada de una exponencial que en su exponente tiene a una función y dicha función es un producto de dos funciones, aunque parezca un trabalenguas la derivada, este tipo de derivadas son comunes en los exámenes.

Debemos de tener en claro la fórmula que aplicaremos:

$\displaystyle \frac{d}{dx}{{e}^{f(x)}}={{e}^{f(x)}}\cdot f'(x)$

Si observamos, debemos derivar la función que sería un producto de dos funciones, si lo hacemos paso a paso tendríamos esto:

$\displaystyle y={{e}^{t\cdot sen(4t)}}\left[ \frac{d}{dx}t\cdot sen(4t)+t\cdot \frac{d}{dx}sen(4t) \right]$

Empezando a derivar a t que es la derivada de una variable, nos daría 1

$\displaystyle y'={{e}^{t\cdot sen(4t)}}\left[ 1\cdot sen(4t)+t\cdot \frac{d}{dx}sen(4t) \right]$

Ahora nos tocaría derivar a sen (4t), recordemos que la derivada de una función seno sería así:

$\displaystyle \frac{d}{dx}sen(u)=u'\cdot sen(u)$

Esto quiere decir que tenemos que derivar a 4t del argumento de seno, para que nuestra derivada original tenga esta forma:

$\displaystyle y'={{e}^{t\cdot sen(4t)}}\left[ 1\cdot sen(4t)+t\cdot \cos (4t)\cdot 4 \right]$

Ordenando nuestra derivada, tenemos:

▶️ Resultado:

$\displaystyle y'={{e}^{t\cdot sen(4t)}}\left[ sen(4t)+4t\cos (4t) \right]$

Ejemplo 5. Resuelva la siguiente derivada

$\displaystyle y={{(1+3{{e}^{5x}})}^{\frac{1}{2}}}$

Solución:

Esta es una derivada de la forma:

$\displaystyle y={{u}^{n}}$

Donde su derivada es:

$\displaystyle y'=n{{u}^{n-1}}\frac{d}{dx}(u)$

Aplicando en nuestra derivada tenemos:

$\displaystyle y'=\frac{1}{2}{{\left( 1+3{{e}^{5x}} \right)}^{-\frac{1}{2}}}\frac{d}{dx}\left( 1+3{{e}^{5x}} \right)$

$\displaystyle y'=\frac{1}{2}{{\left( 1+3{{e}^{5x}} \right)}^{-\frac{1}{2}}}\left( 3{{e}^{5x}}\cdot 5 \right)$

Ordenando

▶️ Resultado:

$\displaystyle y'=\frac{15{{e}^{5x}}}{2\sqrt{1+3{{e}^{5x}}}}$

Ejemplo 6. Resuelva la siguiente derivada

$\displaystyle y=\tan \left( {{e}^{\pi x}} \right)$

Solución:

Se deriva como la derivada de la tangente:

$\displaystyle y'={{\sec }^{2}}\left( {{e}^{\pi x}} \right)\cdot {{e}^{\pi x}}\cdot \pi$

▶️ Resultado:

$\displaystyle y'=\pi {{e}^{\pi x}}{{\sec }^{2}}\left( {{e}^{\pi x}} \right)$

Ejemplo 7. Resuelva la siguiente derivada

$\displaystyle y={{e}^{{{e}^{x}}}}$

Solución:

Se trata de la derivada de una exponencial elevada a una función exponencial, por lo que derivamos:

$\displaystyle y'={{e}^{{{e}^{x}}}}\cdot {{e}^{x}}$

▶️ Resultado:

$\displaystyle y'={{e}^{\left( {{e}^{x}}+1 \right)}}$

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

Deja una respuesta Cancelar la respuesta